阅读量:0
系列文章目录
第二章 【机器学习】【监督学习】- 逻辑回归算法 (Logistic Regression)
第四章【机器学习】【监督学习】- K-近邻算法 (K-NN)
第五章【机器学习】【监督学习】- 决策树 (Decision Trees)
第六章【机器学习】【监督学习】- 梯度提升机 (Gradient Boosting Machine, GBM)
第七章 【机器学习】【监督学习】-神经网络 (Neural Networks)
第十一章【机器学习】【监督学习】-局部加权线性回归 (Locally Weighted Linear Regression, LWLR)
第十二章【机器学习】【监督学习】- 岭回归 (Ridge Regression)
十三、【机器学习】【监督学习】- Lasso回归 (Least Absolute Shrinkage and Selection Operator)
十四、【机器学习】【监督学习】- 弹性网回归 (Elastic Net Regression)
十七、【机器学习】【非监督学习】- K-均值 (K-Means)
十八、【机器学习】【非监督学习】- DBSCAN (Density-Based Spatial Clustering of Applications with Noise)
目录
一、非监督学习
（一）、定义
非监督学习是一种机器学习方法，它处理的是没有标签的数据集。与监督学习不同，非监督学习算法不需要知道数据的正确分类或目标值。它的目标是通过数据内部的结构和模式来推断出有意义的信息，如数据的分布、聚类、降维或异常检测等。
（二）、训练流程
非监督学习的训练流程通常包含以下几个步骤：
数据准备：收集和预处理数据，可能包括数据清洗、缺失值处理、数据标准化或归一化等。
模型选择：根据问题的性质选择合适的非监督学习算法。
参数初始化：初始化模型的参数，这一步对于某些算法至关重要，如K-means聚类。
模型训练：使用无标签数据训练模型，寻找数据中的结构或模式。这一过程可能涉及到迭代优化，直到满足某个停止准则，如收敛或达到预定的迭代次数。
结果评估：评估模型的结果，这通常比监督学习更具有挑战性，因为没有明确的“正确答案”。评估可能基于内在指标（如聚类的紧凑度和分离度）或外在指标（如与已知分类的比较）。
应用模型：使用训练好的模型对新数据进行分析或预测，如对新数据进行聚类或降维。
（三）、基本算法分类
非监督学习算法可以大致分为以下几类：
聚类算法：用于将数据点分组到不同的簇中，常见的算法有K-means、层次聚类、DBSCAN、Gaussian Mixture Models等。
降维算法：用于减少数据的维度，同时尽可能保留数据的结构信息，常见的算法有PCA（主成分分析）、t-SNE（t-分布随机邻域嵌入）、自编码器等。
关联规则学习：用于发现数据集中项之间的关系，如Apriori算法和Eclat算法。
异常检测算法：用于识别数据集中的异常点或离群点，如Isolation Forest、Local Outlier Factor等。
自组织映射（SOM）：一种神经网络模型，用于数据可视化和聚类，可以将高维数据映射到低维空间中。
生成模型：如变分自编码器（VAE）和生成对抗网络（GAN），它们可以生成类似训练数据的新样本。
非监督学习在很多场景中都有广泛应用，如客户细分、图像识别、自然语言处理、生物信息学和推荐系统等。由于其灵活性和在处理大量未标注数据时的优势，非监督学习是数据科学和人工智能领域的重要组成部分。
二、均值漂移 (Mean Shift)
（一）、定义
均值漂移算法是一种无监督学习方法，最初由 Fukunaga 和 Hostetler 在 1975 年提出。它是一种基于密度的聚类算法，用于估计数据的模式（局部最大值），并且不需要事先指定聚类的数量。均值漂移算法在图像处理、计算机视觉、目标跟踪和数据挖掘等领域有着广泛的应用。
（二）、基本概念
均值漂移算法的核心思想是利用数据点的密度来确定聚类中心。算法假设数据点在高密度区域附近聚集，并且这些高密度区域的中心代表了潜在的聚类中心。算法通过迭代地将数据点移动到其邻域内其他点的平均位置（质心）来实现这一点，从而逐渐“漂移”至高密度区域的中心。
（三）、训练过程
均值漂移算法是一种迭代的、基于密度的聚类方法，它能够自动检测数据的高密度区域并确定这些区域的中心，即模式。下面是均值漂移算法的详细训练步骤：
1. 初始化
- 选择一个数据点作为起始点，可以是数据集中的任意点，也可以是随机选择的点。
- 确定带宽参数（bandwidth）h，这是一个核函数的尺度参数，决定了考虑邻域的范围。带宽的选择对算法的性能有很大影响，较小的带宽可能会导致过拟合，较大的带宽可能会忽略数据的细节。
2. 计算偏移向量
- 对于选定的起始点，计算其邻域内所有点的加权平均位置，权重由核函数决定。常用的核函数是高斯核函数：
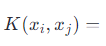
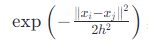其中 𝑥𝑖和 𝑥𝑗分别是数据点，∥𝑥𝑖−𝑥𝑗∥ 表示两点之间的距离。
3. 更新点的位置
- 使用计算出的偏移向量来更新起始点的位置。偏移向量实际上是邻域内所有点的加权平均位置与当前点位置之间的差值。
- 新位置 𝑥𝑛𝑒𝑤可以通过以下公式计算得出：
其中 𝑥x是当前点，𝑁是邻域内的数据点总数。
4. 迭代
- 重复步骤2和3，直到点的位置变化小于一个预定义的阈值或达到最大迭代次数。这意味着点已经收敛到了高密度区域的中心。
5. 应用于所有数据点
- 对数据集中的每一个数据点执行上述过程，直到所有点都收敛到各自高密度区域的中心。
6. 形成聚类
- 当所有点都收敛后，将最终收敛到相同位置的点归为一个聚类。这通常意味着所有到达同一高密度区域中心的点都属于同一个模式或聚类。
7. 聚类后处理
- 可以进一步对形成的聚类进行后处理，例如去除小的聚类、合并相邻的聚类或对聚类进行分类标签的分配。
8.注意事项
- 均值漂移算法对带宽参数 h 的选择非常敏感。太小的 h 可能会导致算法检测到过多的模式，而太大的 h 可能会忽略数据的细节。
- 在处理大规模数据集时，算法的计算成本可能会变得非常高。为了提高效率，可以使用KD树或其他数据结构来加速邻域点的查找，或者使用近似方法来减少计算量。
（四）、特点
- 非参数性：均值漂移算法不需要预先设定聚类的数量，聚类数目由数据的分布自动决定。
- 适应性：可以发现任意形状的聚类，因为它依赖于数据点的局部密度。
- 高效性：对于大数据集，可以通过使用固定宽度的核函数和有效的数据结构（如KD树）来提高效率。
- 多模态检测：均值漂移可以找到多个模式，即多个高密度区域的中心。
（五）、适用场景
- 图像分割：用于图像的区域划分和对象检测。
- 目标跟踪：在视频序列中跟踪移动对象。
- 聚类分析：在没有先验知识的情况下对数据进行分组。
- 异常检测：识别低密度区域的数据点，可能代表异常或噪声。
（六）、扩展
- Kernel Adaptive Mean Shift (KAMS)：通过动态调整核函数的宽度来适应数据的局部特性。
- Mean Shift Variants for Video Background Subtraction：专门针对视频背景减除任务的均值漂移变种。
- Fast Mean Shift Algorithm：优化算法的计算效率，尤其是在大规模数据集上的性能。
三、总结
均值漂移算法因其灵活性和有效性，在许多领域都有重要的应用，尤其是在需要对数据进行无监督聚类和模式识别的场合。
