第四章：决策树_业界新闻

发布时间:2024-07-29 20:03

阅读量:0

1 基本流程

决策树基于“树”结构进行决策
每个“内部结点”对应于某个属性上的“测试”(test)
每个分支对应于该测试的一种可能结果（即该属性的某个取值)
每个“叶结点”对应于一个“预测结果”

学习过程:通过对训练样本的分析来确定“划分属性”（即内部结点所对应的属性)
预测过程:将测试示例从根结点开始,沿着划分属性所构成的“判定测试序列”下行，直到叶结点

策略:“分而治之”(divide-and-conquer)自根至叶的递归过程
在每个中间结点寻找一个“划分”(split or test)属性

三种停止条件:
当前结点包含的样本全属于同一类别，无需划分;
当前属性集为空,或是所有样本在所有属性上取值相同，无法划分;
当前结点包含的样本集合为空，不能划分.

2 划分选择

2.1 信息增益

信息嫡(entropy)是度量样本集合“纯度”最常用的一种指标假定当前样本集合D中第k类样本所占的比例为Pk，则D的信息嫡定义为

$Ent(D)=-\sum_{k=1}^{|y|}p_klog_2p_k$

信息增益直接以信息嫡为基础,计算当前划分对信息嫡所造成的变化

离散属性a的取值： $\left \{ a^1,a^2,...a^V \right \}$

中在a上取值=的样本集合

以属性a对数据集D进行划分所获得的信息增益为：

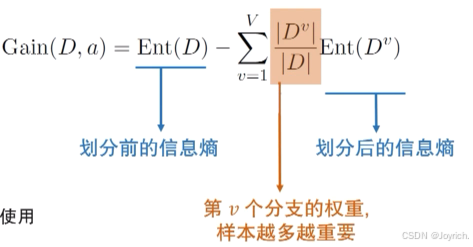
一般而言，信息增益越大,则意味着使用属性α来进行划分所获得的“纯度提升”越大.因此,我们可用信息增益来进行决策树的划分属性选择

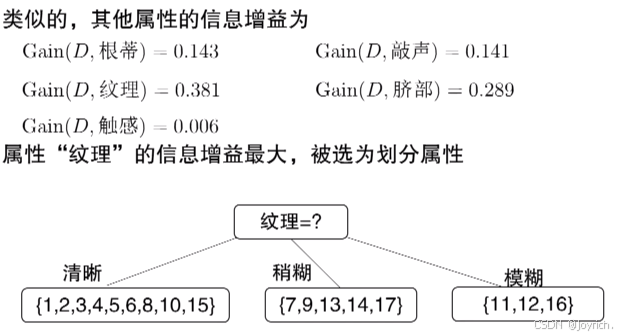
对每个分支结点做进一步的划分，最终得到决策树，如下图所示：

2.2 增益率

如果把编号也作为一个候选划分属性,可计算出它的信息增益为0.998,远大于其他候选划分属性.这很容易理解:“编号”将产生17个分支,每个分支结点仅包含一个样本,这些分支结点的纯度已达最大.然而,这样的决策树显然不具有泛化能力,无法对新样本进行有效预测.

实际上,信息增益准则对可取值数目较多的属性有所偏好,为减少这种偏好可能带来的不利影响,著名的C4.5决策树算法[Quinlan,1993]不直接使用信息增益,而是使用“增益率”(gain ratio)来选择最优划分属性.采用与式(4.2)相同的符号表示,增益率定义为

$Gain_ratio(D,a)=\frac{Gain(D,a)}{IV(a)}$

其中， $IV(a)=-\sum_{v=1}^{V}\frac{|D^v|}{|D|}log_2\frac{|D^v|}{|D|}$

属性a的可能取值数目越多(即V越大)，则IV(a)的值通常就越大

启发式:先从候选划分属性中找出信息增益高于平均水平的，再从中选取增益率最高的

2.3 基尼指数

CART决策树：使用“基尼指数”划分属性

数据集D的纯度可用基尼值来度量：

$Gini(D)=\sum_{k=1}^{|y|}\sum_{k'\neq k}^{}p_kp_{k'}=1-\sum_{k=1}^{|y|}p_k^2$

反映了从D中随机抽取两个样例，其类别标记不一致的概率,Gini(D)越小，数据集D的纯度越高

属性a的基尼指数：

$Gini-index(D,a)=\sum_{v=1}^{V}\frac{|D^v|}{|D|}Gini(D^v)$

在候选属性集合中，选取那个使划分后基尼指数最小的属性

3 剪枝处理

研究表明:划分选择的各种准则虽然对决策树的尺寸有较大影响，但对泛化性能的影响很有限

例如信息增益与基尼指数产生的结果，仅在约2%的情况下不同

剪枝方法和程度对决策树泛化性能的影响更为显著

在数据带噪时甚至可能将泛化性能提升25%

剪枝(pruning)是决策树对付“过拟合”的主要手段!

为了尽可能正确分类训练样本，有可能造成分支过多→过拟合

可通过主动去掉一些分支来降低过拟合的风险

基本策略：

预剪枝(pre-pruning): 提前终止某些分支的生长
后剪枝(post-pruning): 生成一棵完全树，再“回头”剪枝

剪枝过程中需评估剪枝前后决策树的优劣

4 连续与缺失值

4.1 连续值处理

现实应用中，经常会遇到连续属性，由于连续属性的可取值数目不再有限，因此,不能直接根据连续属性的可取值来对结点进行划分.此时,连续属性离散化技术可派上用场.最简单的策略是采用二分法(bi-partition)对连续属性进行处理,这正是C4.5决策树算法中采用的机制[Quinlan,1993].

对连续属性a,我们可考察包含n -1个元素的候选划分点集合

$T_a=\left \{ \frac{a^i+a^{i+1}}{2}|1\leqslant i\leqslant n-1 \right \}$

即把区间 $[a^i,a^{i+1})$ 的中位点 $\frac{a^i+a^{i+1}}{2}$ 作为候选划分点.然后,我们就可像离散属性值一样来考察这些划分点,选取最优的划分点进行样本集合的划分.稍加改造:

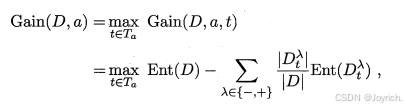
4.2 缺失值处理

现实应用中，经常会遇到属性值“缺失”(missing)现象

仅使用无缺失的样例?→对数据的极大浪费

使用带缺失值的样例，需解决:
Q1:如何进行划分属性选择?
Q2:给定划分属性，若样本在该属性上的值缺失，如何进行划分?

基本思路:样本赋权,权重划分

使用如下图的数据集：

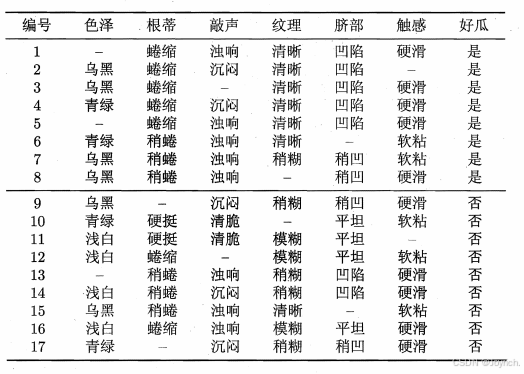
学习开始时，根结点包含样例集D中全部17个样例，权重均为1

以属性“色泽”为例，该属性上无缺失值的样例子集D包含14个样例，信息嫡为：

类似地可计算出所有属性在数据集上的信息增益

在“纹理”上出现缺失值,样本8，10同时进入三个分支，三分支上的权重分别为7/15，5/15，3/15

5 多变量决策树

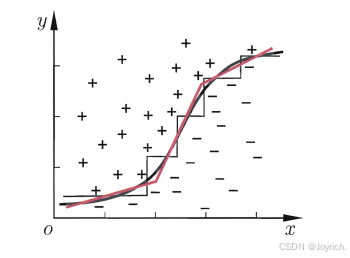
若我们把每个属性视为坐标空间中的一个坐标轴,则d个属性描述的样本就对应了d维空间中的一个数据点;对样本分类则意味着在这个坐标空间中寻找不同类样本之间的分类边界.决策树所形成的分类边界有一个明显的特点:轴平行(axis-parallel)，即它的分类边界由若干个与坐标轴平行的分段组成.

分类边界的每一段都是与坐标轴平行的.这样的分类边界使得学习结果有较好的可解释性,因为每-段划分都直接对应了某个属性取值.但在学习任务的真实分类边界比较复杂时,必须使用很多段划分才能获得较好的近似，

支持

资讯

第四章：决策树

1 基本流程

2 划分选择

2.1 信息增益

2.2 增益率

2.3 基尼指数

3 剪枝处理

4 连续与缺失值

4.1 连续值处理

4.2 缺失值处理

5 多变量决策树

相关阅读

广告一刻