【深度学习】AI修图——DragGAN原理解析

1、前言

上一篇，我们讲述了StyleGAN2。这一篇，我们就来讲一个把StyleGAN2作为基底架构的DragGAN。DragGAN的作用主要是对图片进行编辑，说厉害点，可能和AI修图差不多。这篇论文比较新，发表自2023年

原论文：Drag Your GAN: Interactive Point-based Manipulation on the Generative Image Manifold

参考代码：https://github.com/skimai/DragGAN

视频：AI修图——DragGAN原理解析-哔哩哔哩

演示（随意选择红点，让红点对应位置的像素移动到蓝点）：

demo

2、DragGAN运行原理：

前置知识：StyleGAN（请确保你已经知道这个模型）

DragGAN模型的原理，是构建在StyleGAN的基础上。以下，为StyleGAN的模型图

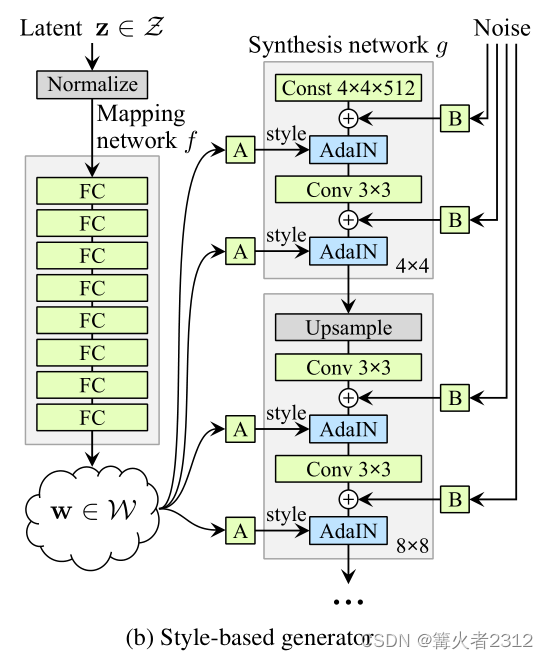
首先，你要有一个训练好的StyleGAN，然后通过该模型，获得一个风格信息w latent Code。接着，用这个风格信息合成图像，如上图的演示，得到狮子的图像。

接着，我们在狮子图像上，选择数量对等的红色点（初始点）和蓝色点（目标点），每一个红色点周围的像素点慢慢移动到对应蓝色点的位置，从而达到修图的效果

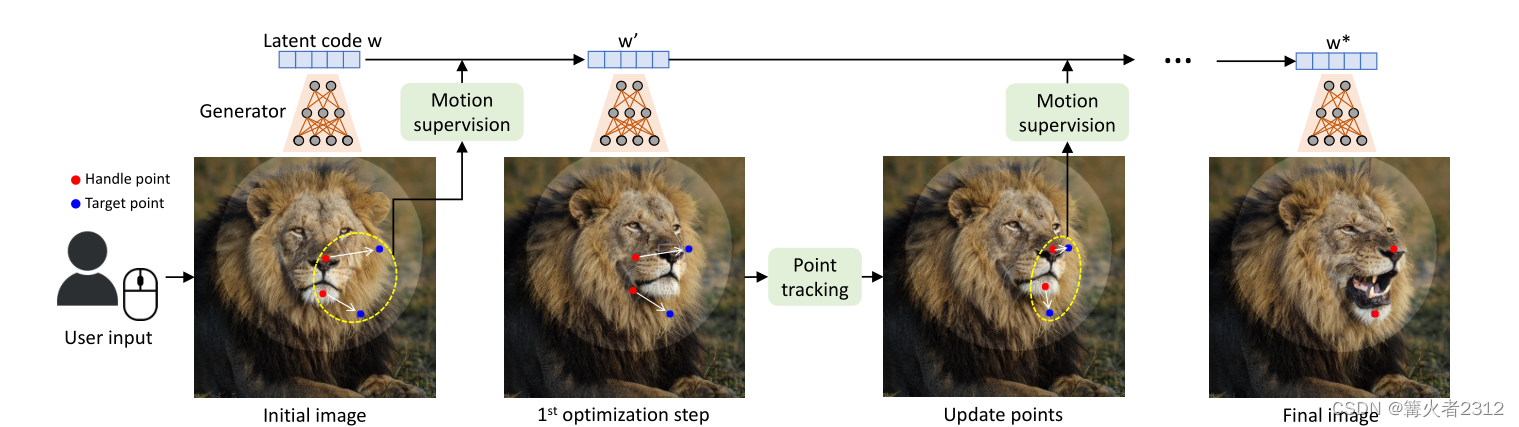
3、实现方法

DragGAN使用的是StyleGAN2，所里里面的风格信息记作w+ latent Code

StyleGAN2的w+ latent Code代表的是风格信息。对图像位置进行移动等等，其实就是风格信息的修改，因此，DragGAN其实就是通过优化w来实现图像的变化。并且，作者通过实验，发现这种空间属性的变化，主要由前6层的w+ latent Code控制，所以作者只优化前6层的w+。

除此之外，作者通过衡量合成网络特征图之间的差异来判断是否初始点达到了目标点。（为了方便，以下所有的w都表示w+）

来看具体流程

①对生成的图像狮子，其有对应风格信息 w latent Code。在图像上选择红色点（初始点，记为p）跟蓝色点（目标点，记为t）。

②找到256x256分辨率的输出特征图（feature map），然后通过双线性插值的方法，将分辨率采样成1024x1024（假设狮子的像素是1024）。如下图的Feature，记为F

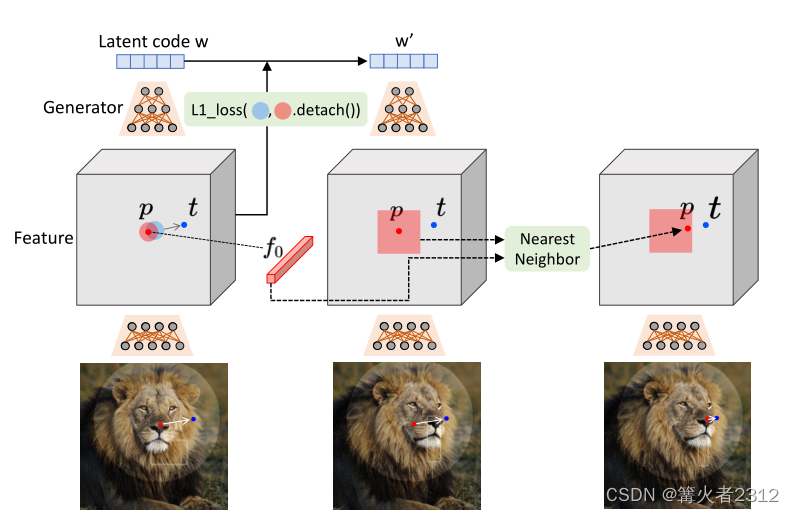
③把在狮子的红色点p和蓝色点t，也同样标记在Feature中，记为$F(p)$，$F(t)$，计算$p$指向$t$的方向向量$d=\frac{t-p}{||t-p|{|}_2}$（分母是对向量归一化）.

④在F§这个位置点，画一个半径为$r_1$的红色小圆，取特征图F里面位置在圆内的所有像素点（红色区域），记其中某一个像素点为$q_i$，并把这个像素点根据方向向量移动，即$F(q_i+d)$

⑤最小化$||F(q_i).detach()-F(q_i+d)|{|}_1$。detach代表$F(q_i)$不反向传播，这会激励$q_i+d$这个位置的值尽量等于$F(q_i)$，而$F(q_i)$代表的刚好是狮子对应位置的特征，所以更新之后会产生移动

⑥对于红色圆区域内的所有点，我们希望它都朝着d的方向移动，所以有最小化
$$\sum _{q_i\in {\Omega }_1(p,r_1)}||F(q_i).detach()-F(q_i+d)|{|}_1$$
​ 其中$\Omega$表示的是红色圆，$q_i$表示属于圆内的像素点。

⑦在实际中，可能不止有一个红色点和蓝色点，可能存在n个，所以
$$\sum _{j=1}^n\sum _{q_i\in {\Omega }_1(p_j,r_1)}||F(q_i).detach()-F(q_i+d_j)|{|}_1$$
⑧DragGAN还允许用户选择图像哪些区域不变，哪些区域改变，则设定区域不变性
$$\sum _{j=1}^n\sum _{q_i\in {\Omega }_1(p_j,r_1)}||F(q_i).detach()-F(q_i+d_j)|{|}_1+\lambda ||(F-F_0)\ast (1-M)|{|}_1$$
​ 其中M是一张与特征图F一样大的矩阵，取值0或1，0代表图像的这个区域不改变，1代表可改变。

⑨对上面的损失函数进行优化更新w风格信息，得到新的$w^{\prime }$，新的特征图$F^{\prime }$。由于梯度下降和方向向量d的正则化的原因，并不能使初始点p一步到位走到目标点t，所以需要从新的特征图$F^{\prime }$找到初始点p已经走到哪里了，我们记初始点为在原始特征图上为$f_i=F_0(p_i)$。

⑩取新的特征图$F^{\prime }$，在初始点p这个位置画一个变长为$r_2$红色正方形（图中第二个特征图），把正方形内的像素点与$F_0(p_i)$作最近邻搜索，长得最像的那个就是皮卡丘，将其作为新的初始点，即
$$p_i:=\underset{q_i\in {\Omega }_2(p_i,r_2)}{\mathrm{argmin}}||F^{\prime }(q_i)-f_i|{|}_1$$
​ $:=$表示将右边的所得最小对应变量值赋给等式左边

迭代更新，最终使得初始点到达点t点，结束

看不明白？那就看视频吧，文字所能传达的信息有限。我尽力了，私密马赛

4、结束

以上就是DragGAN这篇论文的全部内容了，如有问题，还望指出，阿里嘎多！