【C++高阶】哈希之美：探索位图与布隆过滤器的应用之旅

avatar
作者
猴君
阅读量:0

📝个人主页🌹：Eternity._
⏩收录专栏⏪：C++ “ 登神长阶 ”
🤡往期回顾🤡：模拟实现unordered 的奥秘
🌹🌹期待您的关注 🌹🌹

在这里插入图片描述

在这里插入图片描述
在这里插入图片描述

❀哈希应用

前言：在数据科学的浩瀚星空中，哈希函数犹如一颗璀璨的星辰，以其独特的光芒照亮了数据处理的每一个角落。哈希，这一简单而强大的技术，通过将任意长度的输入（如字符串、数字等）映射到固定长度的输出（即哈希值），实现了数据的快速定位与索引。然而，哈希的魅力远不止于此，当它与位图和布隆过滤器相结合时，更是催生出了一系列高效且实用的数据处理方案

位图（Bitmap）但是库里面：bitset，作为一种基于位操作的数据结构，以其极低的内存占用和高效的查询性能，在数据去重、频繁项集挖掘等领域展现出了非凡的潜力。通过将数据映射到位图的特定位上，我们可以实现快速的数据检索和统计，极大地提升了数据处理的速度和效率。

而布隆过滤器（Bloom Filter），则是在位图的基础上进一步创新的杰作。它通过引入多个哈希函数和位数组的组合，巧妙地实现了对大量数据的高效检索和去重，同时允许一定程度的误判率，从而在空间效率和查询速度之间取得了完美的平衡。布隆过滤器的这一特性，使得它在网络爬虫去重、垃圾邮件过滤、数据库索引优化等多个领域得到了广泛的应用。

本文将带您踏上一场探索哈希应用、位图与布隆过滤器的旅程。我们将从哈希函数的基本原理出发，逐步深入到位图和布隆过滤器的内部工作机制，通过生动的案例和详细的解释，让您了解这些技术是如何相互协作，共同解决现实世界中的复杂问题的

让我们一起踏上学习的旅程，探索它带来的无尽可能！

📒1. 位图

🌄位图的概念

我们直接介绍位图的话，大家可能没那么好理解，我们先通过一道面试题来带领大家，看看位图的应用场景

面试题：
在这里插入图片描述
解决办法：

  • 遍历，时间复杂度O(N)
  • 排序(O(NlogN))，利用二分查找: logN
  • 位图解决

大家在没学习位图之前，通常会用前两个方法来解决这个问题，但是前两个办法真的能够解决吗？对于这种海量数据，可能我们在使用前两种办法时，根本没有这么多的空间给你使用，因此我们就搞出了位图这个东西

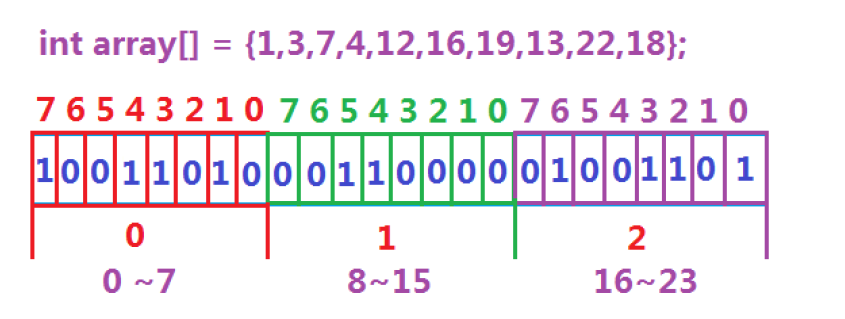
位图解决：数据是否在给定的整形数据中，结果是在或者不在，刚好是两种状态，那么可以使用一个二进制比特位来代表数据是否存在的信息，如果二进制比特位为1，代表存在，为0代表不存在
在这里插入图片描述

所谓位图，就是用每一位来存放某种状态，适用于海量数据，数据无重复的场景。通常是用
来判断某个数据存不存在的

位图的应用：

  • 快速查找某个数据是否在一个集合中
  • 排序 + 去重
  • 求两个集合的交集、并集等
  • 操作系统中磁盘块标记

🏞️位图的实现

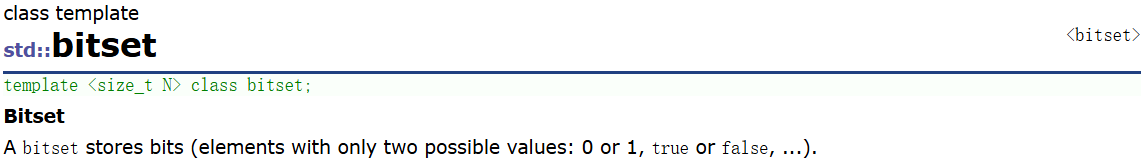
在这里插入图片描述

代码示例 (C++)：

template<size_t N> class bitset { public: 	// 构造函数 	bitset() 	{ 		_bits.resize(N / 32 + 1, 0); 	} 	// ...... 其他待实现的函数 private: 	vector<int> _bits; };

关于位图的模拟实现，我们只需要将它最常用的3个函数实现就够用了

  • set：将一个数据放入位图中
  • reset：将一个数据从位图中删掉
  • test：检测一个数据在不在位图中

set的模拟实现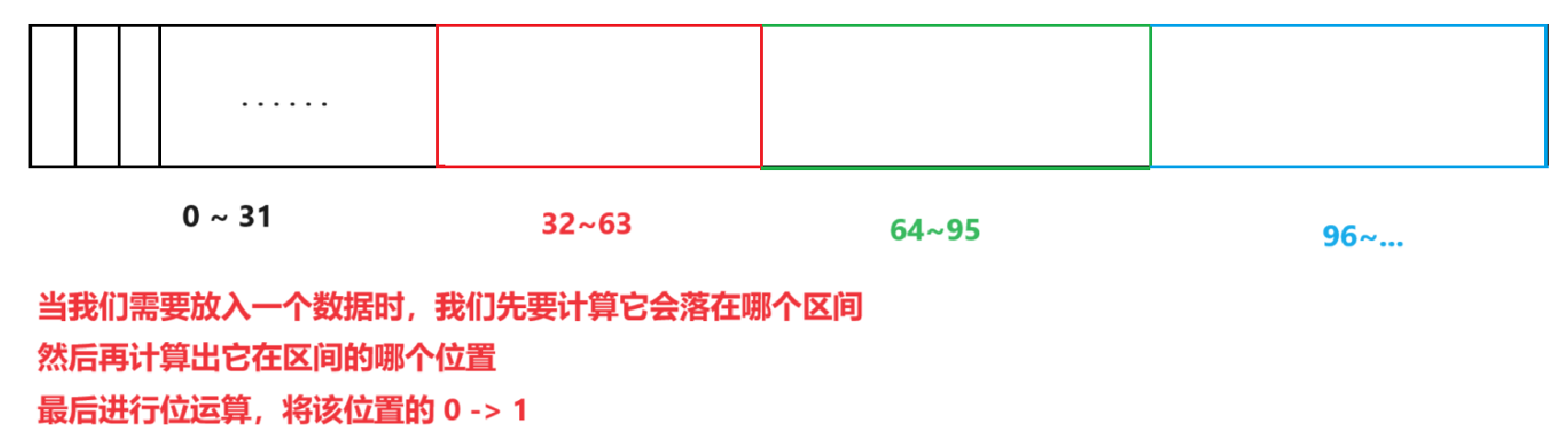
在这里插入图片描述
最后的运算我们也只需要将1移位过去进行|运算

reset的模拟实现

reset的模拟实现和set只需要将最后一步反过来：1 -> 0，但是我们没有办法将0进行移位，所以我们依旧是将1移位过去进行，但是在运算前我们进行~取反，然后进行&运算

test的模拟实现

test的模拟实现我们只需要判断该数据的映射位置是否为1就行，还是比较简单的

代码实现 (C++)：

template<size_t N> class bitset { public: 	bitset() 	{ 		// 构造函数，我们在需要的空间基础上 +1 		_bits.resize(N / 32 + 1, 0); 	}  	void set(size_t x) 	{ 		size_t i = x / 32; 		size_t j = x % 32; 		_bits[i] |= (1 << j); 	}  	void reset(size_t x) 	{ 		size_t i = x / 32; 		size_t j = x % 32; 		_bits[i] &= ~(1 << j); 	}  	bool test(size_t x) 	{ 		size_t i = x / 32; 		size_t j = x % 32; 		return _bits[i] & (1 << j); 	} private: 	vector<int> _bits; };

📜2. 布隆过滤器

我们在使用新闻客户端看新闻时，它会给我们不停地推荐新的内容，它每次推荐时要去重，去掉那些已经看过的内容。问题来了，新闻客户端推荐系统如何实现推送去重的？ 用服务器记录了用户看过的所有历史记录，当推荐系统推荐新闻时会从每个用户的历史记录里进行筛选，过滤掉那些已经存在的记录。 如何快速查找呢?

  • 用哈希表存储用户记录，缺点：浪费空间
  • 用位图存储用户记录，缺点：位图一般只能处理整形，如果内容编号是字符串，就无法处理了
  • 将哈希与位图结合，即布隆过滤器

🌈布隆过滤器概念

布隆过滤器是由布隆（Burton Howard Bloom）在1970年提出的 一种紧凑型的、比较巧妙的概率型数据结构，特点是高效地插入和查询，可以用来告诉你 “某样东西一定不存在或者可能存在”，它是用多个哈希函数，将一个数据映射到位图结构中。此种方式不仅可以提升查询效率，也可以节省大量的内存空间

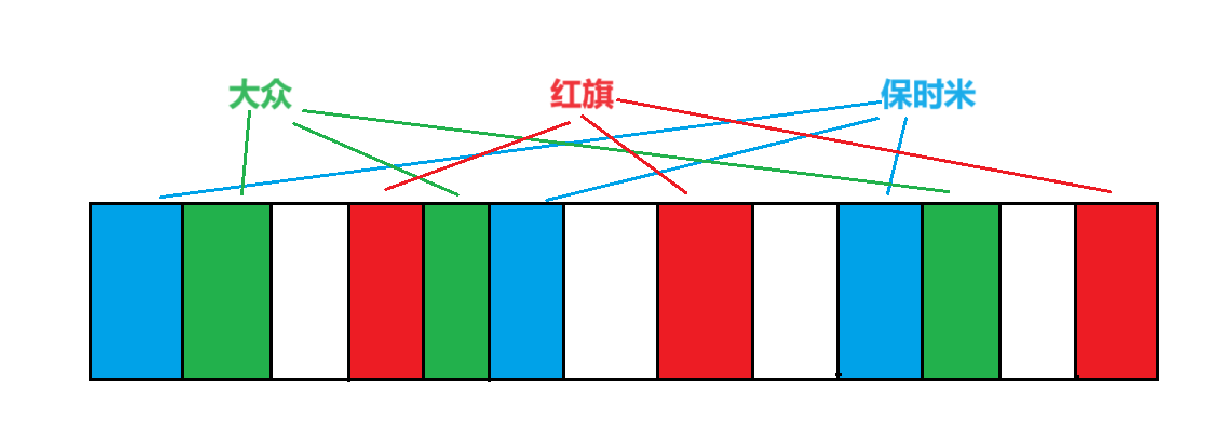
在这里插入图片描述
在这里插入图片描述

代码示例 (C++)：

template<size_t N, class K = string> class BloomFilter { public: 	// ...... 其他待实现的函数 private: 	bitset<N> _bs; }

注意：布隆过滤器的底层是上面讲到的位图

如果想要更深入的了解可以阅读一下这篇文章：
布隆过滤器详解

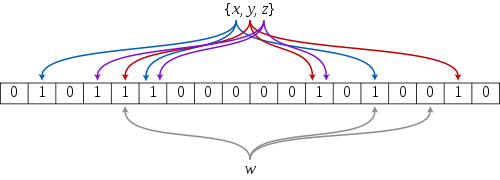
🌞布隆过滤器的插入

布隆过滤器的应用通常是string类型的参数，因此我们需要和之前哈希一样，将他们转化成整形，而布隆过滤器一般会映射到3个位置，因此我们会有3个不同仿函数来计算

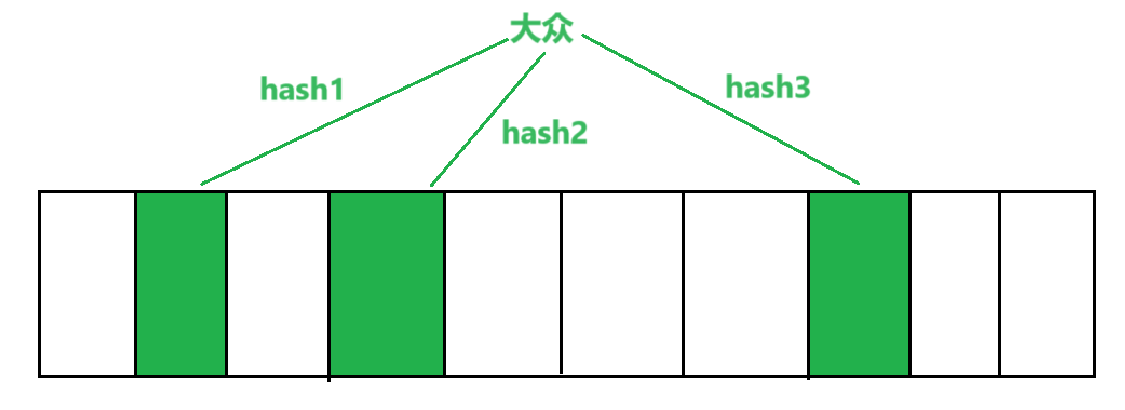
在这里插入图片描述

仿函数示例 (C++)：

struct BKDRHash { 	size_t operator()(const string& key) 	{ 		size_t hash = 0; 		for (auto e : key) 		{ 			e *= 31; 			hash += e; 		} 		return hash; 	} };   struct APHash { 	size_t operator()(const string& key) 	{ 		size_t hash = 0; 		size_t ch; 		for (size_t i = 0; i < key.size(); i++) 		{ 			ch = key[i]; 			if ((i & 1) == 0) 			{ 				hash ^= ((hash << 7) ^ ch ^ (hash >> 3)); 			} 			else 			{ 				hash ^= (~((hash << 11) ^ ch ^ (hash >> 5))); 			} 		} 		return hash; 	} };  struct DJBHash { 	size_t operator()(const string& key) 	{ 		size_t hash = 5381; 		for (auto ch : key) 		{ 			hash += (hash << 5) + ch; 		} 		return hash; 	} };

插入代码示例 (C++)：

void Set(const K& key) { 	size_t hash1 = HashFunc1()(key) % N; 	size_t hash2 = HashFunc2()(key) % N; 	size_t hash3 = HashFunc3()(key) % N;  	_bs.set(hash1); 	_bs.set(hash2); 	_bs.set(hash3); }

🌙布隆过滤器的查找

分别计算每个哈希值对应的比特位置存储的是否为零，只要有一个为零，代表该元素一定不在哈希表中，否则可能在哈希表中

注意：布隆过滤器如果说某个元素不存在时，该元素一定不存在，如果该元素存在时，该元素可能存在，因为有些哈希函数存在一定的误判

查找代码示例 (C++)：

bool Test(const K& key) { 	// 判断不存在时准确的 	size_t hash1 = HashFunc1()(key) % N; 	if (_bs.test(hash1) == false) 		return false;  	size_t hash2 = HashFunc2()(key) % N; 	if (_bs.test(hash2) == false) 		return false;  	size_t hash3 = HashFunc3()(key) % N; 	if (_bs.test(hash3) == false) 		return false;  	// 存在误判 	return true; }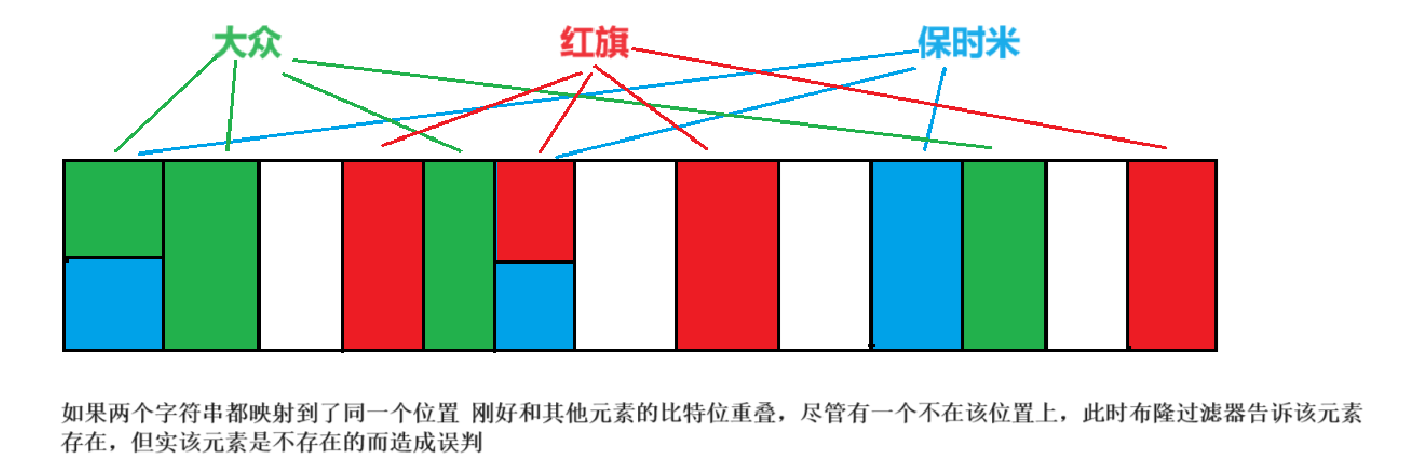

在这里插入图片描述

布隆过滤器如果说某个元素不存在时，该元素一定不存在
如果该元素存在时，该元素可能存在

⭐布隆过滤器的优点和缺陷

优点：

  • 增加和查询元素的时间复杂度为:O(K), (K为哈希函数的个数，一般比较小)，与数据量大小无
    关
  • 哈希函数相互之间没有关系，方便硬件并行运算
  • 布隆过滤器不需要存储元素本身，在某些对保密要求比较严格的场合有很大优势
  • 在能够承受一定的误判时，布隆过滤器比其他数据结构有这很大的空间优势
  • 数据量很大时，布隆过滤器可以表示全集，其他数据结构不能
  • 使用同一组散列函数的布隆过滤器可以进行交、并、差运算

缺陷：

  • 有误判率，即存在假阳性(False Position)，即不能准确判断元素是否在集合中(补救方法：再
    建立一个白名单，存储可能会误判的数据)
  • 不能获取元素本身
  • 一般情况下不能从布隆过滤器中删除元素
  • 如果采用计数方式删除，可能会存在计数回绕问题

📚3. 海量数据题目

🧩哈希切分

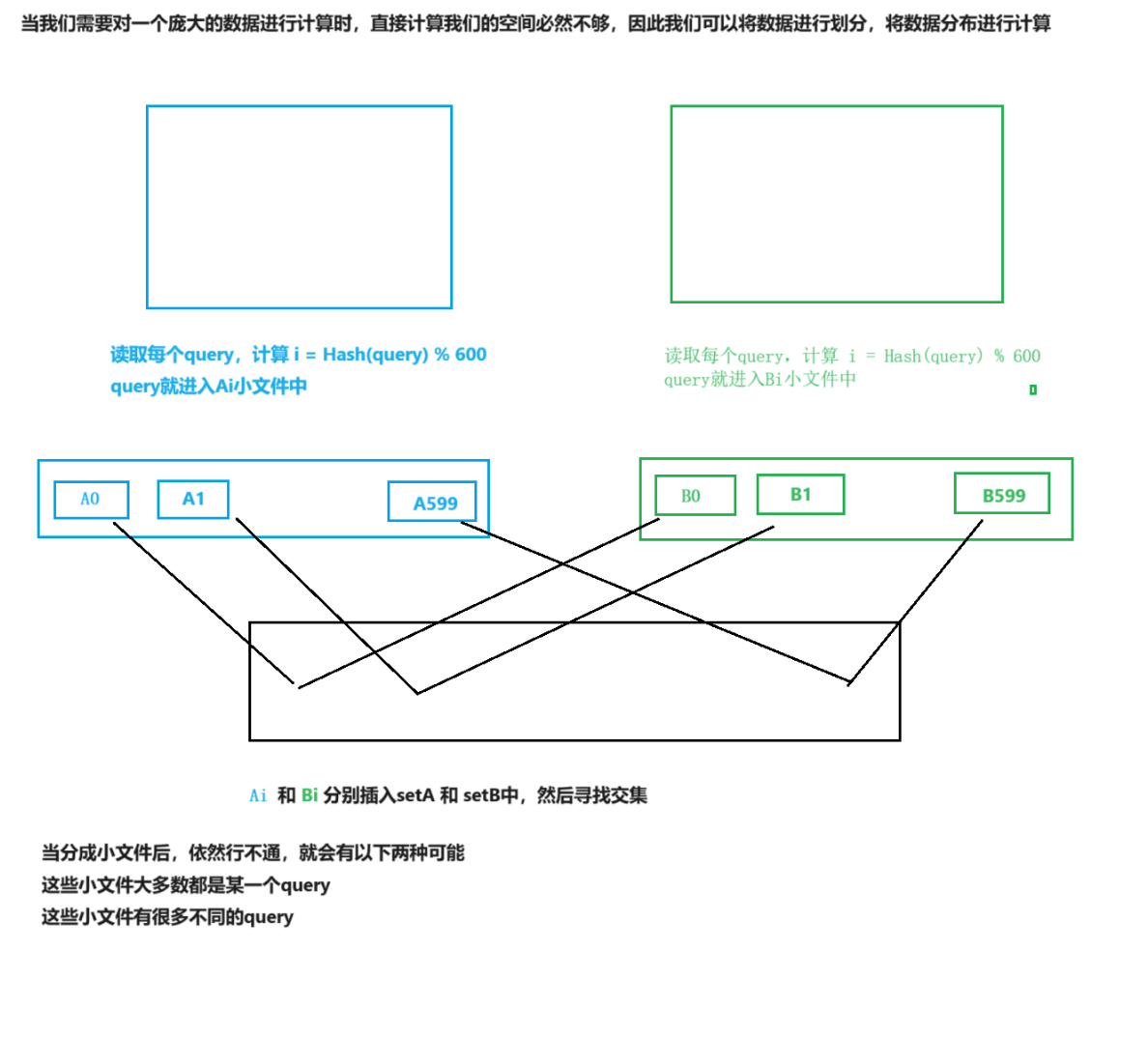
在这里插入图片描述
不管文件大小，我们都是直接读取到内存，然后插入set

  • 情况一：文件很多重复，后面重复插入都是失败，因此我们可以直接插入到set中
  • 情况二：不断插入set后，内存不足，会抛异常，因此我们要换哈希函数，进行二次切分

位图应用：

  • 给定100亿个整数，设计算法找到只出现一次的整数？
  • 给两个文件，分别有100亿个整数，我们只有1G内存，如何找到两个文件交集？
  • 位图应用变形：1个文件有100亿个int，1G内存，设计算法找到出现次数不超过2次的所有整
    数

布隆过滤器：

  • 给两个文件，分别有100亿个query，我们只有1G内存，如何找到两个文件交集？分别给出
    精确算法和近似算法
  • 如何扩展BloomFilter使得它支持删除元素的操作

📖4. 总结

随着我们对哈希应用、位图与布隆过滤器的深入探讨，不难发现，这些技术不仅仅是数据科学工具箱中的简单工具，它们更是智慧与创新的结晶，为数据的快速处理、高效检索和精确去重提供了强有力的支持

哈希函数以其独特的映射能力，为我们打开了一扇通往高效数据处理的大门。而位图，则以其极低的内存占用和快速的查询性能，成为了处理大规模数据集时的得力助手。至于布隆过滤器，它更是在继承位图优势的基础上，通过引入哈希函数的组合，实现了对大量数据的快速检索与去重，虽然伴随着一定的误判率，但其在空间效率与查询速度之间的精妙平衡，让它在众多应用场景中大放异彩

随着数据量的持续增长和数据处理需求的日益复杂，我们有理由相信，哈希应用、位图与布隆过滤器等高效数据处理技术将会得到更加广泛的应用和深入的研究。它们将继续在数据科学的舞台上发光发热，为我们揭示更多数据背后的秘密和价值

我们期待每一位读者都能从本次探索中汲取到宝贵的知识和经验，保持对新技术、新知识的好奇心和求知欲，不断探索、不断学习、不断进步
在这里插入图片描述
希望本文能够为你提供有益的参考和启示，让我们一起在编程的道路上不断前行！
谢谢大家支持本篇到这里就结束了，祝大家天天开心！

在这里插入图片描述

相关阅读
  1. 项目推荐：Scribe —— 高效的日志聚合服务器
  2. ctf之双色块
  3. GPU服务器与CPU服务器的不同之处
  4. 探索D3Status：暴雪《暗黑破坏神3》服务器状态的智能守护者
  5. Oracle同一台服务器创建多个数据库
  6. WEB应用服务器 -- Tomcat详解及案例实现
  7. 云服务器与传统服务器的区别是什么？
  8. WEB前端10- Fetch API(同步/异步/跨域处理)
  9. 腾讯云 Nginx 服务器 SSL 证书安装部署（Windows）
  10. Intern LM-入门岛-LESSON1-LINUX基础知识

广告一刻

为您即时展示最新活动产品广告消息，让您随时掌握产品活动新动态！