🎯要点
🎯分层结构制定生成模型 | 🎯贝叶斯模型选择程序 | 🎯分层结构图的信息性 | 🎯分层模型适应实值边协变量的网络 | 🎯分层模型适应时变网络,划分层对应于检测变化点 | 🎯定义两种版本随机块模型:🖊具有边缘协变量模型概率分布,分层图总似然 | 🖊独立分层模型分层图数学似然计算 | 🎯推理算法:大图形尺度并行计算算法,过滤暂时被遮蔽的节点和边
📜分层图算法和统计推理用例
📜C++和R穿刺针吸活检肿瘤算法模型模拟和进化动力学量化差异模型
📜Python和MATLAB网络尺度结构和幂律度大型图生成式模型算法
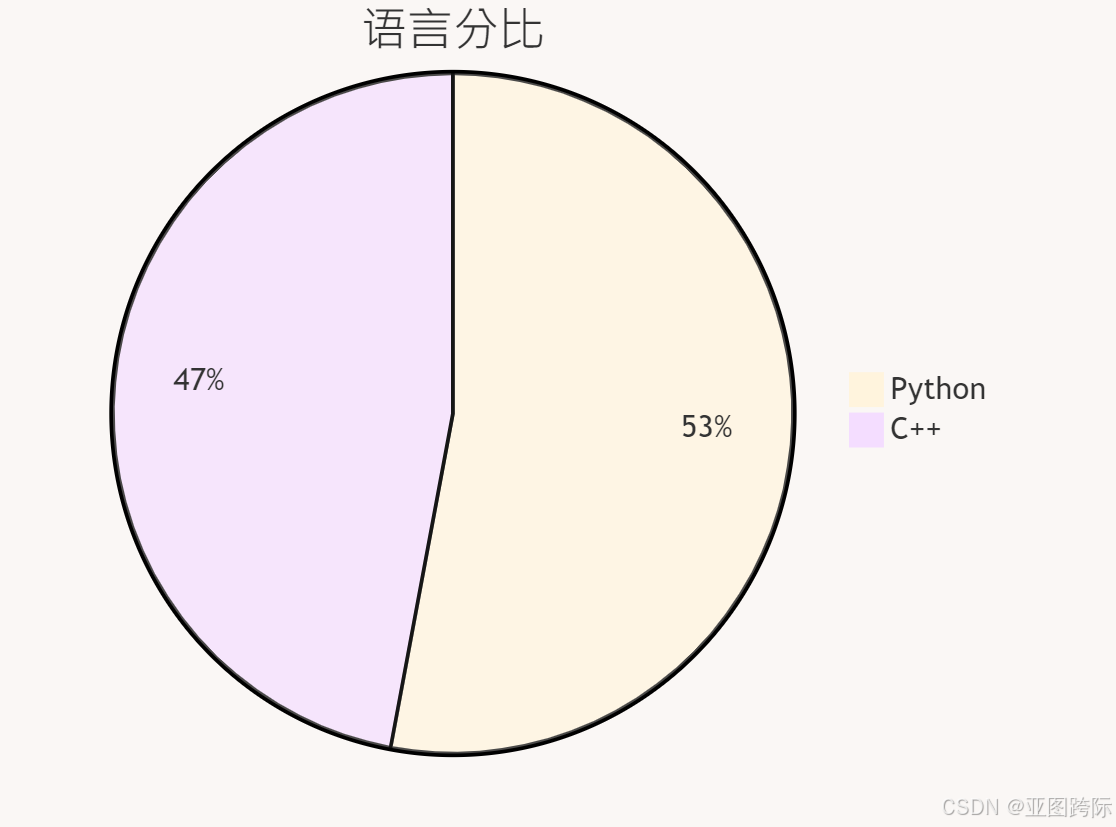
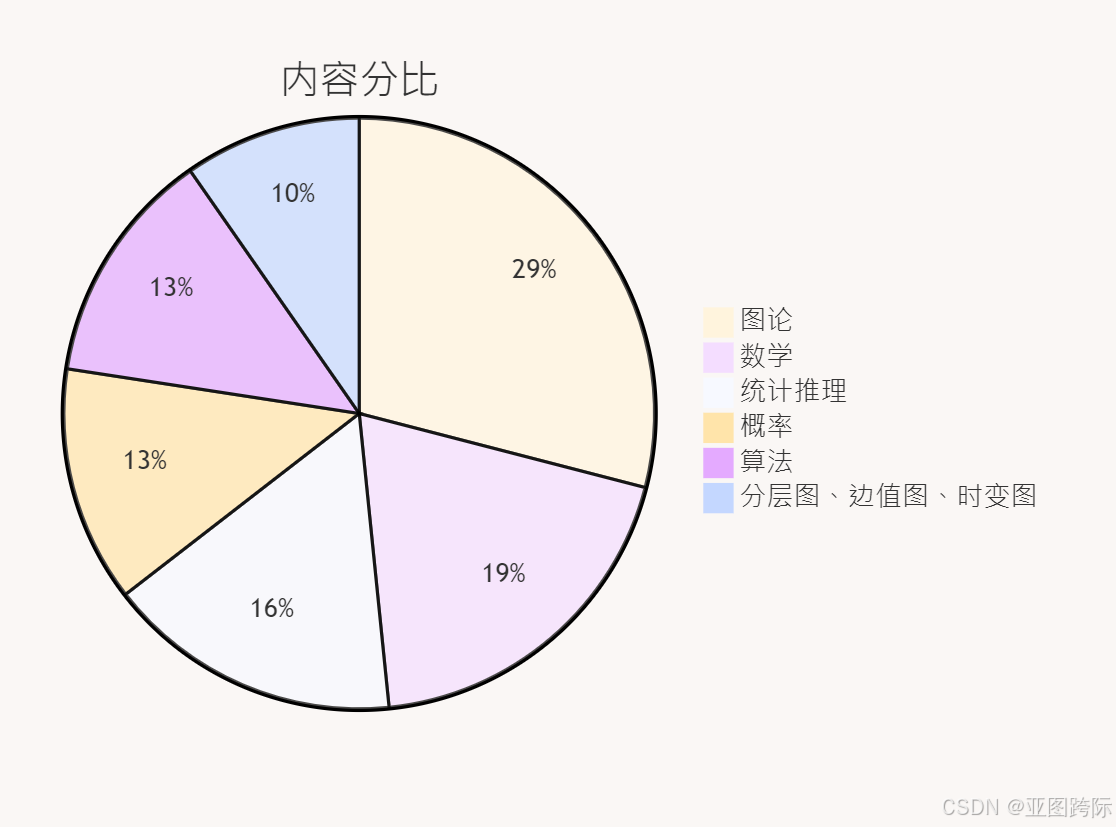
🍪语言内容分比
🍇Python交通图模拟
假设我们的业务正在以惊人的速度增长。我们希望通过在 G.nodes 代表的当地城镇之一张贴广告牌来扩大我们的客户群。为了最大限度地提高广告牌的浏览量,我们将选择交通最繁忙的城镇。直观地说,交通量是由每天经过城镇的汽车数量决定的。我们可以根据预期的每日交通量对 G.nodes 中的 31 个城镇进行排序,使用简单的建模,我们可以从城镇之间的道路网络预测交通流量。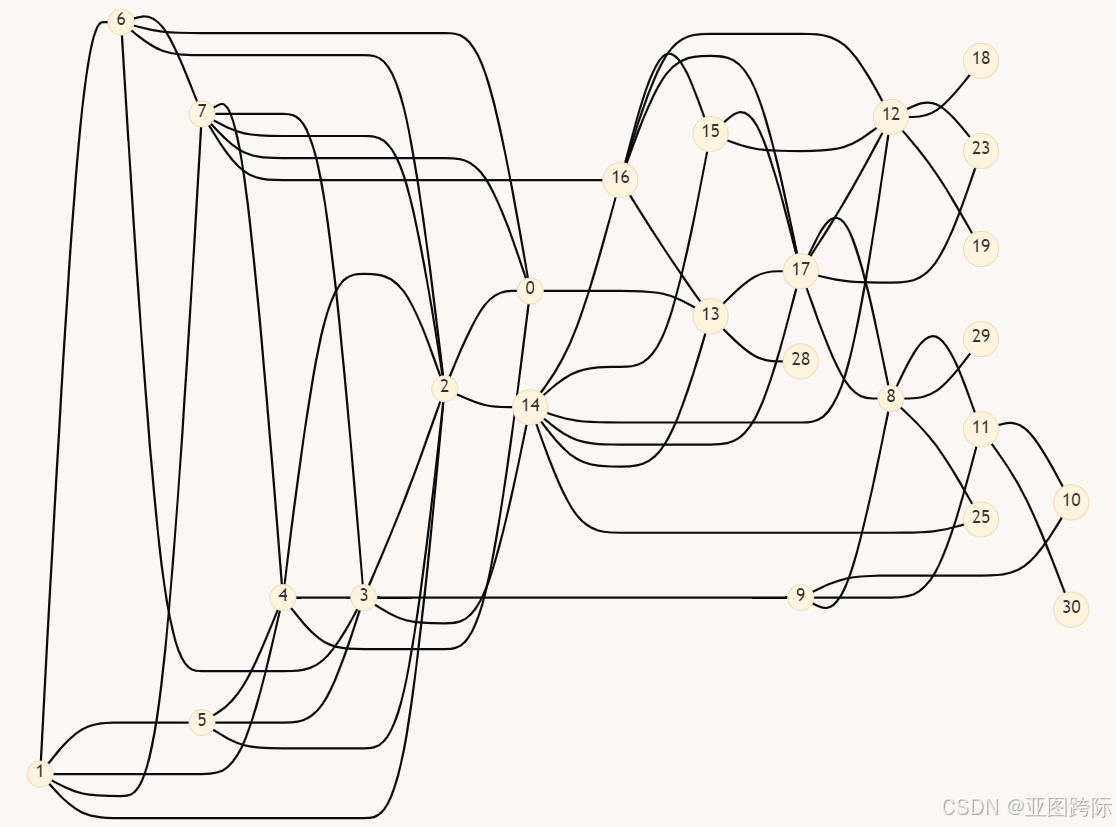
我们需要一种根据预期流量对城镇进行排名的方法。简单来说,我们可以简单地计算每个城镇的入站道路数:拥有五条道路的城镇可以接收来自五个不同方向的交通,而只有一条道路的城镇的交通流量则更为有限。节点的入度是指向节点的有向边的数量。但是,与网站图不同,我们的道路网络是无向的:入站边和出站边之间没有区别。因此,节点的入度和出度之间没有区别;这两个值相等,因此无向图中节点的边数简称为节点的度。我们可以通过对图的邻接矩阵的第 i 列求和来计算任何节点 i 的度,或者我们可以通过运行 len(G.nodes[i]) 来测量度。或者,我们可以通过调用 G.degree(i) 来利用 NetworkX 度方法。在这里,我们利用所有这些技术来计算经过 0 号镇的道路数量。
计算单个节点的度
adjacency_matrix = nx.to_numpy_array(G) degree_town_0 = adjacency_matrix[:,0].sum() assert degree_town_0 == len(G[0]) assert degree_town_0 == G.degree(0) print(f"Town 0 is connected by {degree_town_0:.0f} roads.") Town 0 is connected by 5 roads. 使用节点的度数,我们根据重要性对节点进行排序。在图论中,任何衡量节点重要性的指标通常称为节点中心性,而根据节点度数对重要性进行排序则称为中心度。现在,我们选择 G 中中心度最高的节点:这个中心节点将作为我们广告牌位置的初始选择。
使用中心度选择中心节点
np.random.seed(1) central_town = adjacency_matrix.sum(axis=0).argmax() degree = G.degree(central_town) print(f"Town {central_town} is our most central town. It has {degree} " "connecting roads.") node_colors[central_town] = 'k' nx.draw(G, with_labels=True, node_color=node_colors) plt.show() Town 3 is our most central town. It has 9 connecting roads. 镇 3 是我们最中心的城镇。道路将其连接到九个不同的城镇和三个不同的县。镇 3 与第二中心城镇相比如何?我们将通过输出 G 中第二高的度来快速检查。
选择中心度第二高的节点
second_town = sorted(G.nodes, key=lambda x: G.degree(x), reverse=True)[1] second_degree = G.degree(second_town) print(f"Town {second_town} has {second_degree} connecting roads.") Town 12 has 8 connecting roads. 城镇 12 有 8 条连接道路,仅落后城镇 3 一条道路。如果这两个城镇的度数相等,我们会怎么做?在图 中,我们看到一条连接城镇 3 和城镇 9 的道路。假设这条道路因失修而关闭。关闭需要移除 G 中的一条边。运行 G.remove(3, 9) 会移除节点 3 和 9 之间的边,因此城镇 3 的度数会变为与城镇 12 的度数相等。网络还发生了其他重要的结构变化。在这里,我们将这些变化可视化
从最中心的节点移除一条边
np.random.seed(1) G.remove_edge(3, 9) assert G.degree(3) == G.degree(12) nx.draw(G, with_labels=True, node_color=node_colors) plt.show() 模拟单车随机路线
np.random.seed(0) def random_drive(num_stops=10): town = np.random.choice(G.nodes) for _ in range(num_stops): town = np.random.choice(G[town]) return town destination = random_drive() print(f"After driving randomly, the car has reached Town {destination}.") After driving randomly, the car has reached Town 24. 使用 20,000 辆汽车模拟交通
import time np.random.seed(0) car_counts = np.zeros(len(G.nodes)) num_cars = 20000 start_time = time.time() for _ in range(num_cars): destination = random_drive() car_counts[destination] += 1 central_town = car_counts.argmax() traffic = car_counts[central_town] running_time = time.time() - start_time print(f"We ran a {running_time:.2f} second simulation.") print(f"Town {central_town} has the most traffic.") print(f"There are {traffic:.0f} cars in that town.") We ran a 3.47 second simulation. Town 12 has the most traffic. There are 1015 cars in that town. 检查 3 号镇的交通情况
print(f"There are {car_counts[3]:.0f} cars in Town 3.") There are 934 cars in Town 3. 将客流量计数转换为概率
probabilities = car_counts / num_cars for i in [12, 3]: prob = probabilities[i] print(f"The probability of winding up in Town {i} is {prob:.3f}.") The probability of winding up in Town 12 is 0.051. The probability of winding up in Town 3 is 0.047. 根据我们的随机模拟,我们将有 5.1% 的时间到达 12 号镇,而只有 4.7% 的时间到达 3 号镇。因此,表明 12 号镇比 3 号镇更靠近中心。
