Tensorflow中高维矩阵的乘法运算tf.matmul(tf.linalg.matmul)详悉

1.问题由来

 在tensorflow框架下，经常会用到矩阵的乘法运算，特别是高（多）维的矩阵运算，在这些矩阵运算时，经常使用到其中的tf.matmul或tf.linalg.matmul等函数。但高维矩阵在内部怎么运算的？其内部的参数是怎么实现的在tensorflow给出的介绍仍然存在表达不明的问题，所以在此作进一步的阐释。

声明：本博客里的数组乘法运算是指矩阵乘法运算，不是对应元素相乘。所述高维代表矩阵的维度3维。

2.高维矩阵的乘法运算规则

2.1 运算条件

两矩阵的维数相同： 
前个维度都一致：
最后两个维度满足矩阵乘法运算：
具体地，假设 ，，则 能运算的条件如下图（箭头表示相等）：

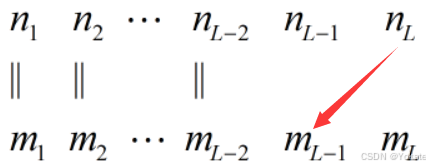
 2.2 使用tf.matmul(tf.linalg.matmul)时存在的问题

 按照上文的规则使用tf.matmul(tf.linalg.matmul)时，又会存在各种问题。以tf.linalg.matmul为例，其关键参数设置如下，和表征2个高维矩阵，transpose_a和transpose_b可以理解为分别对和这2个矩阵的转置操作。我们假设和都是4维矩阵，并设维度分别为和。tensorflow中，第1维一般是batchsize。那么，tf.linalg.matmul(a,b,transpose_b=True)是不是对矩阵的真正转置呢？即tf.linalg.matmul(a,b,transpose_b=True)是维度维的矩阵与维度为的矩阵直接的矩阵运算呢？

tf.linalg.matmul(     a,     b,     transpose_a=False,     transpose_b=False,     adjoint_a=False,     adjoint_b=False,     a_is_sparse=False,     b_is_sparse=False,     output_type=None,     grad_a=False,     grad_b=False,     name=None )

 如果我们直接看tensorflow给出的解释如下

 直观的理解确实如前文所述，其实不然。

这里的transpose_a / transpose_b=True并不是执行传统数学意义上的转置操作，而是仅对高维矩阵上的最后两个维度的转置，其它维度仍保持不变。这是通过调用tf.linalg.matrix_transpose实现的。具体如下

tf.linalg.matrix_transpose(     a, name='matrix_transpose', conjugate=False )

tensorflow文档中对其的描述如下，即转置矩阵的最后2个维度。

Transposes last two dimensions of tensor a.

至于后续的运算可以在相关文档中查阅得到。

参考文档

tensorflow中高维数组乘法运算_高位矩阵乘法 tensorflow-CSDN博客

TensorFlow中矩阵乘操作tf.matmul(或tf.linalg.matmul)和矩阵元素乘tf.multiply(或tf.math.multiply)用法对比-CSDN博客