文章目录
题目描述
题目链接:91.解码方法

算法原理
类似于斐波那契数列~
1.状态表示
根据以往的经验,对于⼤多数线性 dp ,我们经验上都是以某个位置结束或者开始做⽂章,这⾥我们继续尝试⽤ i 位置为结尾结合题⽬要求来定义状态表⽰。
dp[i] 表⽰:字符串中 [0,i] 区间上,⼀共有多少种编码⽅法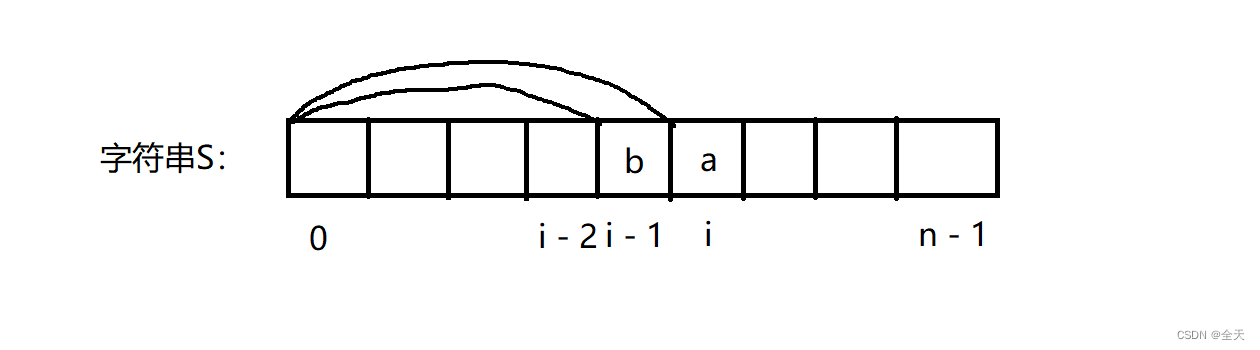
2.状态转移方程
定义好状态表⽰,我们就可以分析 i 位置的 dp 值,如何由前面或者后面的信息推导出来。接下来根据最近一步,划分问题。
关于 i 位置的编码状况,我们可以分为下⾯两种情况:
- 让 i 位置上的数单独解码成⼀个字⺟;
- 让 i 位置上的数与 i - 1 位置上的数结合,解码成⼀个字⺟。
下⾯我们就上⾯的两种解码情况,继续分析。
让 i 位置上的数单独解码成⼀个字⺟,就存在解码成功和解码失败两种情况:
- 解码成功:当 i 位置上的数在 [1, 9] 之间的时候,说明 i 位置上的数是可以单独解码的,那么此时 [0, i] 区间上的解码⽅法应该等于 [0, i - 1] 区间上的解码⽅法。因为 [0, i - 1] 区间上的所有解码结果,后⾯填上⼀个 i 位置解码后的字⺟就可以了。此时 dp[i] = dp[i - 1] ;
- 解码失败:当 i 位置上的数是 0 的时候,说明 i 位置上的数是不能单独解码的,那么此时 [0, i] 区间上不存在解码⽅法。因为 i 位置如果单独参与解码,但是解码失败了,那么前⾯做的努⼒就全部⽩费了。此时 dp[i] = 0 。
让 i 位置上的数与 i - 1 位置上的数结合在⼀起,解码成⼀个字⺟,也存在解码成功和解码失败两种情况:
解码成功:当结合的数在 [10, 26] 之间的时候,说明 [i - 1, i] 两个位置是可以解码成功的,那么此时 [0,i] 区间上的解码⽅法应该等于 [0, i - 2 ] 区间上的解码⽅法,原因同上。此时 dp[i] = dp[i - 2] ;
解码失败:当结合的数在 [0, 9] 和 [27 , 99] 之间的时候,说明两个位置结合后解码失败(这⾥⼀定要注意 00 01 02 03 04 … 这⼏种情况),那么此时 [0, i] 区间上的解码⽅法就不存在了,原因依旧同上。此时 dp[i] = 0 。
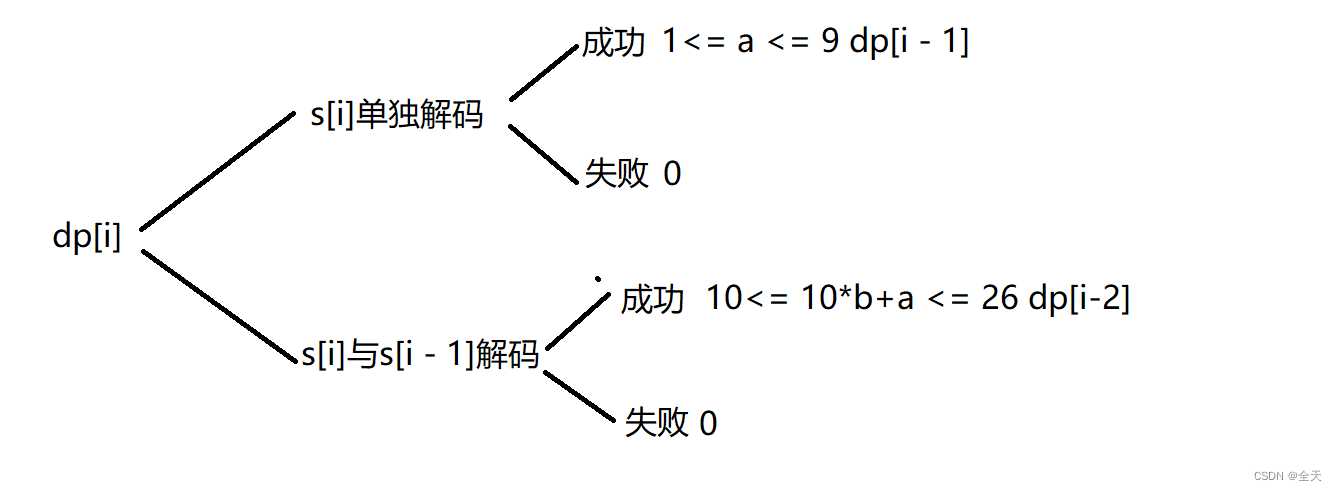
综上所述: dp[i]( dp[i] 默认初始化为 0 )最终的结果应该是上⾯四种情况下,解码成功的两种的累加和(因为我们关⼼的是解码⽅法,既然解码失败,就不⽤加⼊到最终结果中去),因此可以得到状态转移⽅程
//当s[i]上的数在[1, 9]区间上时:dp[i] += dp[i - 1]; //当s[i - 1]与s[i]上的数结合后,在[10, 26]之间的时候:dp[i] += dp[i - 2]; //如果上述两个判断都不成⽴,说明没有解码⽅法,dp[i]就是默认值 0 3.初始化
⽅法⼀(直接初始化)
由于可能要⽤到 i - 1 以及 i - 2 位置上的 dp 值,因此要先初始化前两个位置。
初始化 dp[0] :
- 当 s[0] == ‘0’ 时,没有编码⽅法,结果 dp[0] = 0;
- 当 s[0] != ‘0’ 时,能编码成功, dp[0] = 1;
初始化 dp[1] :
- 当 s[1] 在 [1,9] 之间时,能单独编码,此时 dp[1] += dp[0] (原因同上,dp[1] 默认为 0);
- 当 s[0] 与 s[1] 结合后的数在 [10, 26] 之间时,说明在前两个字符中,⼜有⼀种编码⽅式,此时 dp[1] += 1;
⽅法⼆(添加辅助位置初始化)
可以在最前⾯加上⼀个辅助结点,帮助我们初始化。使⽤这种技巧要注意两个点:
- 辅助结点⾥⾯的值要保证后续填表是正确的;
- 下标的映射关系;
4.填表顺序
毫无疑问是从左往右。
5.返回值
应该返回 dp[n - 1] 的值,表⽰在 [0, n - 1] 区间上的编码⽅法。
代码实现
C++
class Solution { public: int numDecodings(string s) { //1.创建dp表 int n = s.size(); vector<int> dp(n); //2.初始化 dp[0] = s[0] != '0';//字符串s中只含数字 if(n == 1)return dp[0];//处理边界情况 int t = (s[0] - '0') * 10 + (s[1] - '0');//前两个位置所表示的数 if(t >= 10 && t <= 26)dp[1]++;//去除前导0的情况 if(s[0] != '0' && s[1] != '0')dp[1]++; if(n == 2)return dp[1]; //3.填表 for(int i = 2;i < n;++i){ if(s[i] != '0')dp[i] += dp[i - 1];//处理单独编码的情况 int tmp = (s[i - 1] - '0') * 10 + (s[i] - '0');//第二种情况所对应的数 if(tmp >= 10 && tmp <= 26)dp[i] += dp[i - 2]; } //4.返回值 return dp[n - 1]; } }; 优化
使⽤添加辅助结点的⽅式初始化:
class Solution { public: int numDecodings(string s) { // 优化 int n = s.size(); vector<int> dp(n + 1); dp[0] = 1; // 保证后续填表是正确的 dp[1] = s[0] != '0'; // 填表 for (int i = 2; i <= n; i++) { // 处理单独编码 if (s[i - 1] != '0') dp[i] += dp[i - 1]; // 如果和前⾯的⼀个数联合起来编码 int t = (s[i - 2] - '0') * 10 + s[i - 1] - '0'; if (t >= 10 && t <= 26) dp[i] += dp[i - 2]; } return dp[n]; } }; Java
class Solution { public int numDecodings(String ss) { // 1. 创建 dp 表 // 2. 初始化 // 3. 填表 // 4. 返回值 int n = ss.length(); char[] s = ss.toCharArray(); int[] dp = new int[n]; if (s[0] != '0') dp[0] = 1; // 初始化第⼀个位置 if (n == 1) return dp[0]; // 处理边界情况 // 初始化第⼆个位置 if (s[1] != '0' && s[0] != '0') dp[1] += 1; int t = (s[0] - '0') * 10 + s[1] - '0'; if (t >= 10 && t <= 26) dp[1] += 1; for (int i = 2; i < n; i++) { // 先处理第⼀种情况 if (s[i] != '0') dp[i] += dp[i - 1]; // 处理第⼆种情况 int tt = (s[i - 1] - '0') * 10 + s[i] - '0'; if (tt >= 10 && tt <= 26) dp[i] += dp[i - 2]; } return dp[n - 1]; } } 优化
class Solution { public int numDecodings(String ss) { // 1. 创建 dp 表 // 2. 初始化 // 3. 填表 // 4. 返回值 int n = ss.length(); char[] s = ss.toCharArray(); int[] dp = new int[n + 1]; dp[0] = 1; // 保证后续填表是正确的 if (s[1 - 1] != '0') dp[1] = 1; for (int i = 2; i <= n; i++) { // 先处理第⼀种情况 if (s[i - 1] != '0') dp[i] += dp[i - 1]; // 处理第⼆种情况 int tt = (s[i - 2] - '0') * 10 + s[i - 1] - '0'; if (tt >= 10 && tt <= 26) dp[i] += dp[i - 2]; } return dp[n]; } } 