💕"趁着年轻,做一些比较cool的事情"💕
作者:Lvzi
文章主要内容:算法系列–动态规划–背包问题(1)–01背包介绍
大家好,今天为大家带来的是
算法系列--动态规划--背包问题(1)--01背包介绍
一.什么是背包问题
背包问题是动态规划中经典的一类问题,经常在笔试面试中出现,是非常具有区分度的题目
背包问题的种类很多,变式多,也就使得背包问题的难度一般都很高,而01背包问题属于其中最基础,可以当做思考模版的题目,下面就来讲解–01背包问题
前情提示:如果你没有动态规划的基础,还是尽量不要通过背包问题入门,先去做上几十到动态规划的题目再来学习背包问题
二.01背包问题
链接:
01背包问题
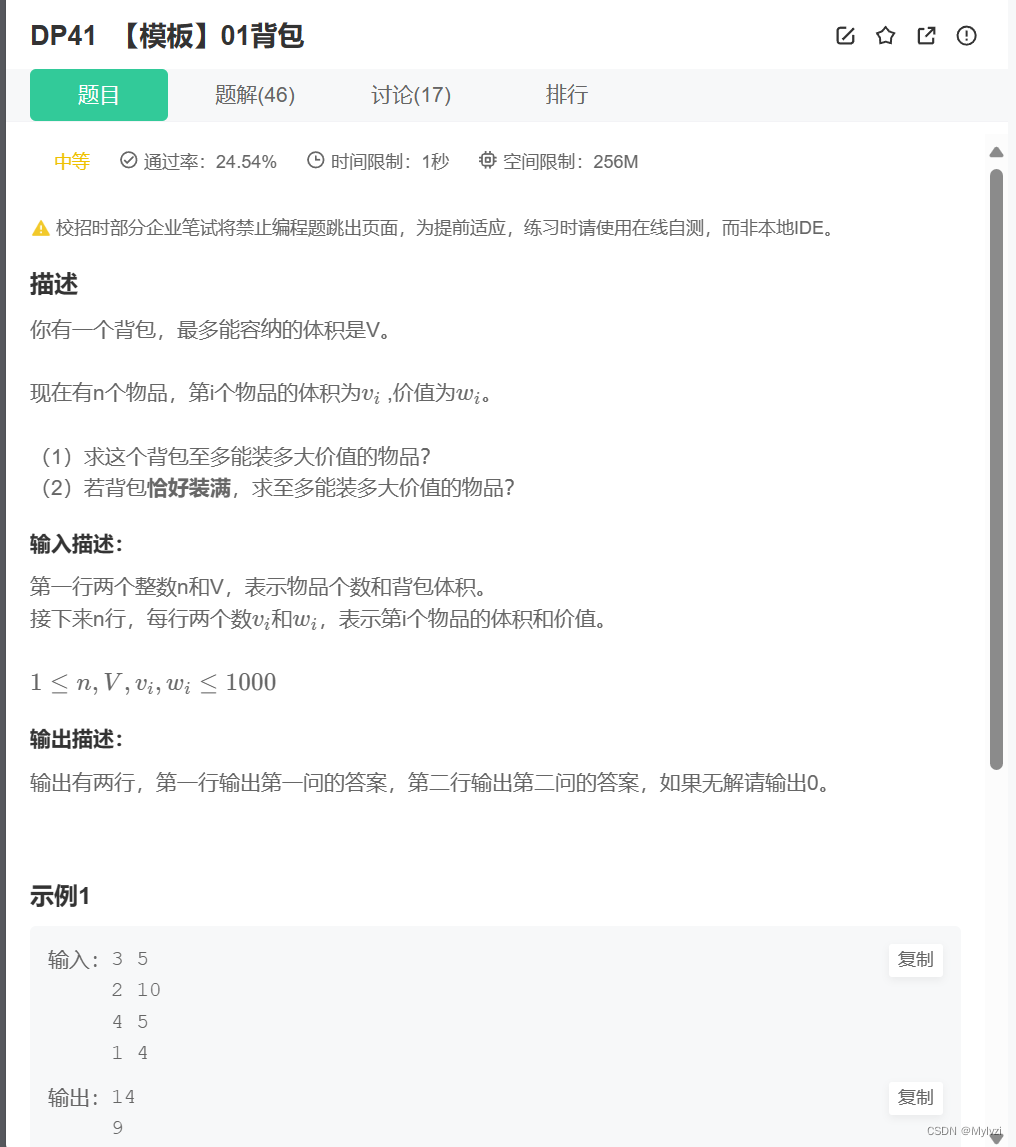
分析:
首先要明确这道题目一共有两问,第一问求的是在不超过背包限制的前提下,可以得到的最大价值
,第二问求的是在刚好装满背包的情况下,可以得到的最大价值
第一问:求这个背包至多能装多大价值的物品?
我们先来模拟一下背包问题的执行过程,其实就是从所有物品中选择合适的物品填入背包,来实现价值的最大化,在选物品时我们是可以任意选择的,这不就类似于在任意的子序列中,选出最大xxxx的问题么?
好了,相信大家也能分析到这里,说:这不就是一个简单的子序列问题么,这有啥难得,于是兴致勃勃的写下状态表示
dp[i]:表示在[1,i]之间的所有物品中,可以实现的最大价值物品的价值
(注:下标我们从1开始是因为这是dp问题常用的一种初始化dp表的方式)
但是我们在填i位置的值时,需要考虑此时背包容量对我们装填的影响(比如如果背包的容量很小,只有1,而我们i物品的体积是99,肯定无法装进去)
所以我们还需要一个状态来表示背包体积,也就是每走到一个物品都要保证符合容量大小,于是状态表示如下:
dp[i][j]:在[1,i]之间的所有物品中,体积不超过j,可以实现的最大价值物品的价值
我们可以验证一下这个状态表示能否返回最终的结果呢?可以,dp[n][V]就表示在所给定的n个物品中,体积不超过背包的最大体积V,选择可以实现最大价值的物品的价值
接下来就来推到状态转移方程:
状态转移方程一般就是根据最后一个位置的状态去讨论,在本题中,分类讨论的依据就是包不包括最后一个物品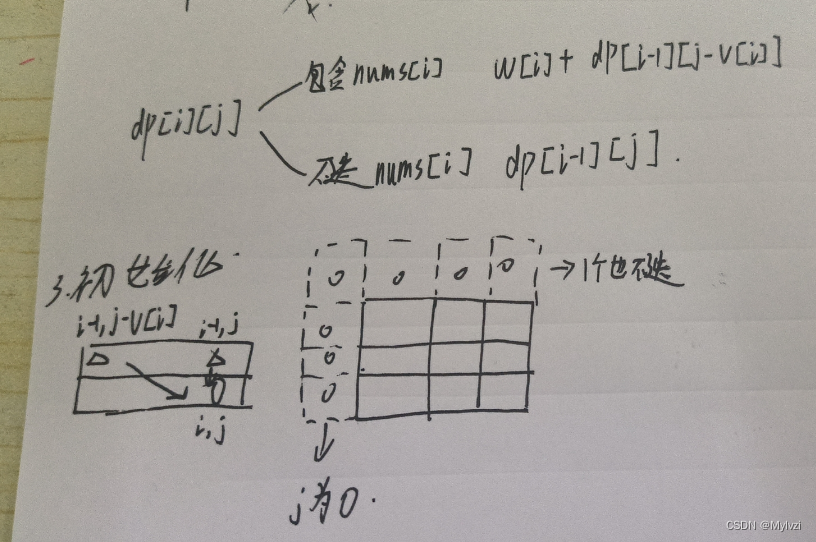
注意:选nums[i]这种情况不是一定能实现的,需要满足此时的背包体积大于第i个物品的体积,也就是需要满足j - v[i] >= 0
返回值:dp[n][V]
以上就是第一问的详细分析过程
第二问:若背包恰好装满,求至多能装多大价值的物品?
相较于第一问多了体积的限制,必须要满足体积的前提下实现价值的最大化,但是大致的思路和第一问很像,只需要在第一问的基础上做出一些改变即可:
dp[i][j]:表示在[0,i]区间内的物品,在体积为j的前提下,可以实现的最大价值
状态转移方程
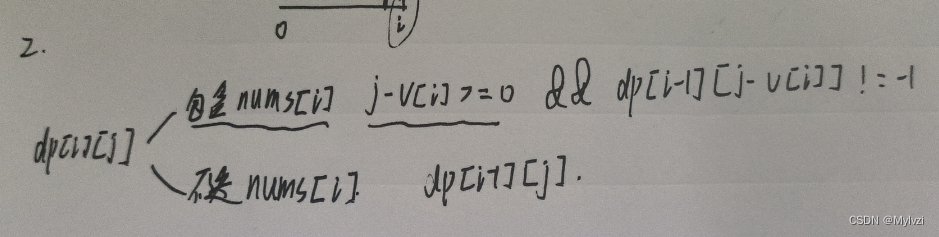
这里多了个限制条件dp[i - 1][j - v[i]] != -1,还是根据题目要求得来的,要考虑一种特殊情况,也就是在[0,i]区间内的物品根本无法组合成体积为j的情况(这也是会存在的),要想i位置存在价值,必须保证i-1位置刚好能够实现j-v[i]的体积
初始化相较于第一问也有所不同,具体来说需要把dp表的第一行初始化为-1(除了dp[0][0]),第一行代表不选择任何物品,也就无法构成满足j体积这个条件,我们将其设置为-1
之所以设置为-1是为了和dp[0][0] = 0这种情况作区分
代码:
import java.util.Scanner; // 注意类名必须为 Main, 不要有任何 package xxx 信息 public class Main { static int N = 1010; public static void main(String[] args) { Scanner in = new Scanner(System.in); int n = in.nextInt(), V = in.nextInt();// 获取物品数目和背包体积 // 处理第一问 int[] v = new int[N],w = new int[N];// 存储物品的体积和价值 for(int i = 1; i <= n; i++) {// 输入数值 v[i] = in.nextInt(); w[i] = in.nextInt(); } int[][] dp = new int[N][N]; for(int i = 1; i <= n; i++) { for(int j = 1; j <= V; j++) { dp[i][j] = dp[i - 1][j]; if(j - v[i] >= 0) dp[i][j] = Math.max(dp[i - 1][j],dp[i - 1][j - v[i]] + w[i]); } } System.out.println(dp[n][V]); // 处理第二问 dp = new int[N][N]; for(int j = 1; j <= V; j++) {// 初始化 dp[0][j] = -1; } for(int i = 1; i <= n; i++) { for(int j = 1; j <= V; j++) { dp[i][j] = dp[i - 1][j]; if(j - v[i] >= 0 && dp[i - 1][j - v[i]] != -1) dp[i][j] = Math.max(dp[i - 1][j],dp[i - 1][j - v[i]] + w[i]); } } System.out.println(dp[n][V] == -1 ? 0 : dp[n][V]); } } 上述解法的空间复杂度是很高的,我们开辟的dp表是一个N*N的,下面介绍使用滚动数组实现空间优化
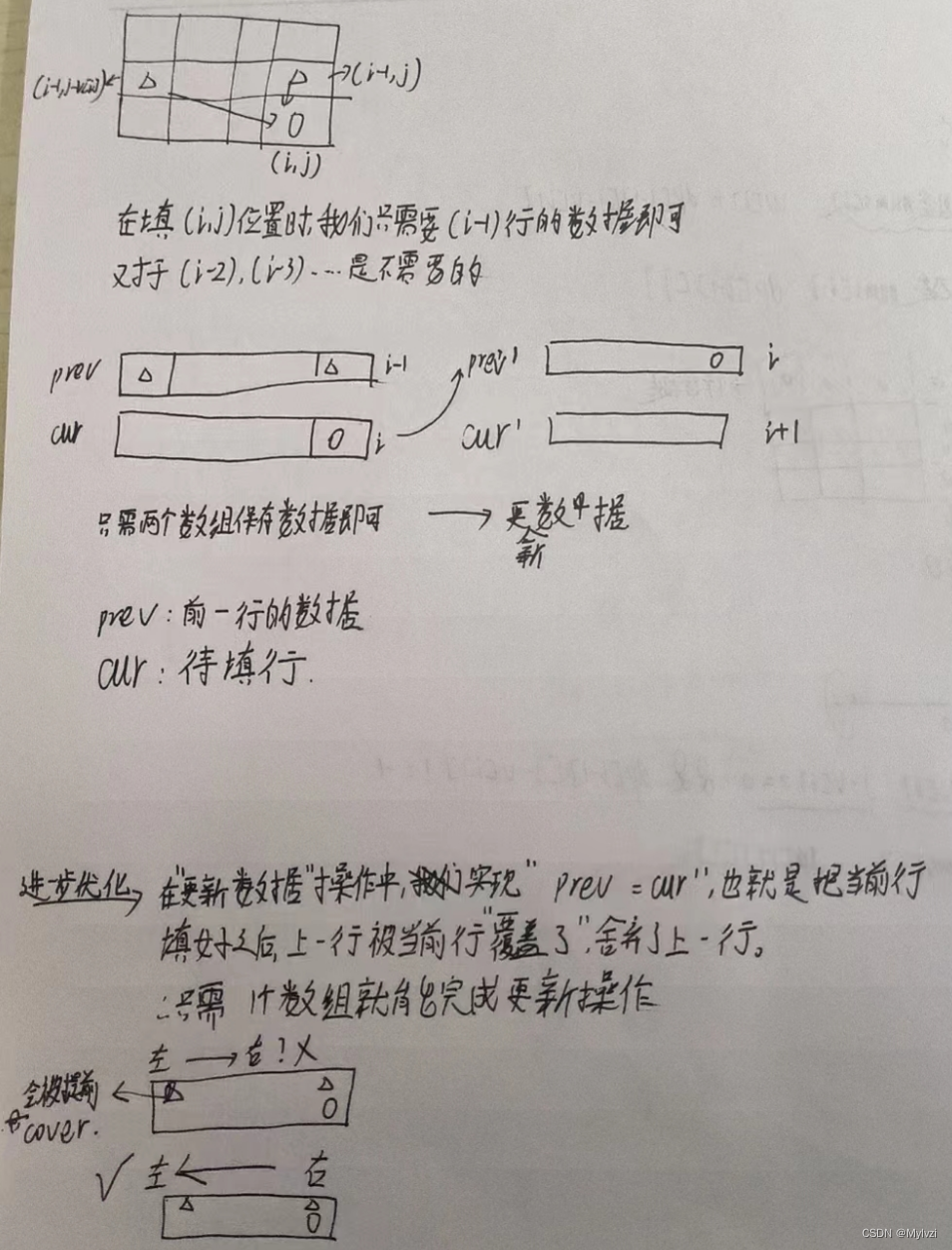
空间优化之后的代码:
import java.util.Scanner; // 注意类名必须为 Main, 不要有任何 package xxx 信息 public class Main { static int N = 1010; public static void main(String[] args) { Scanner in = new Scanner(System.in); int n = in.nextInt(), V = in.nextInt();// 获取物品数目和背包体积 // 处理第一问 int[] v = new int[N],w = new int[N];// 存储物品的体积和价值 for(int i = 1; i <= n; i++) {// 输入数值 v[i] = in.nextInt(); w[i] = in.nextInt(); } int[] dp = new int[N]; for(int i = 1; i <= n; i++) for(int j = V; j >= v[i]; j--) dp[j] = Math.max(dp[j],dp[j - v[i]] + w[i]); System.out.println(dp[V]); // 处理第二问 dp = new int[N]; for(int j = 1; j <= V; j++) dp[j] = -1;// 初始化 for(int i = 1; i <= n; i++) for(int j = V; j >= v[i]; j--) if(j - v[i] >= 0 && dp[j - v[i]] != -1) dp[j] = Math.max(dp[j],dp[j - v[i]] + w[i]); System.out.println(dp[V] == -1 ? 0 : dp[V]); } } 总结:本文的核心要点
- 什么是背包问题
- 01背包问题详解
- 背包问题的空间优化(滚动数组)
以上就是
算法系列--动态规划--背包问题(1)--01背包介绍全部内容,下一篇文章将会带来01背包问题的拓展题目,敬请期待,我是LvZi

