代码随想录算法训练营第57天|647. 回文子串|516.最长回文子序列|动态规划总结篇
今天 我们就要结束动态规划章节了,大家激不激动!!!
详细布置
647. 回文子串
动态规划解决的经典题目,如果没接触过的话,别硬想 直接看题解。
https://programmercarl.com/0647.%E5%9B%9E%E6%96%87%E5%AD%90%E4%B8%B2.html
class Solution { public: int countSubstrings(string s) { vector<vector<bool>>dp(s.size(),vector<bool>(s.size(),false)); int result=0; for(int i=s.size()-1;i>=0;i--) { for(int j=i;j<s.size();j++) { if(s[i]==s[j]) { if(j-i<=1) { result++; dp[i][j]=true; } else if(dp[i+1][j-1]) { result++; dp[i][j]=true; } } } } return result; } }; 总结
也就是对一维数组整体,通过二维数组来求,切记一定用一维数组形象来求3种情况。
确定递推公式
在确定递推公式时,就要分析如下几种情况。
整体上是两种,就是s[i]与s[j]相等,s[i]与s[j]不相等这两种。
当s[i]与s[j]不相等,那没啥好说的了,dp[i][j]一定是false。
当s[i]与s[j]相等时,这就复杂一些了,有如下三种情况
情况一:下标i 与 j相同,同一个字符例如a,当然是回文子串
情况二:下标i 与 j相差为1,例如aa,也是回文子串
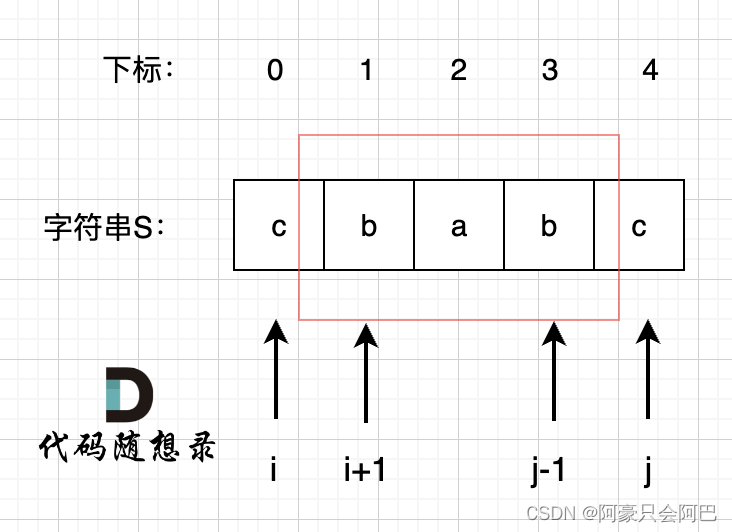
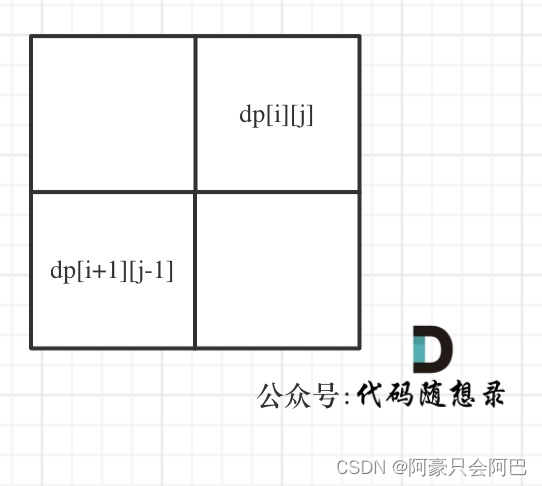
情况三:下标:i 与 j相差大于1的时候,例如cabac,此时s[i]与s[j]已经相同了,我们看i到j区间是不是回文子串就看aba是不是回文就可以了,那么aba的区间就是 i+1 与 j-1区间,这个区间是不是回文就看dp[i + 1][j - 1]是否为true。
516.最长回文子序列
647. 回文子串,求的是回文子串,而本题要求的是回文子序列, 大家要搞清楚两者之间的区别。
https://programmercarl.com/0516.%E6%9C%80%E9%95%BF%E5%9B%9E%E6%96%87%E5%AD%90%E5%BA%8F%E5%88%97.html
class Solution { public: int longestPalindromeSubseq(string s) { vector<vector<int>>dp(s.size(),vector<int>(s.size(),0)); for(int i=0;i<s.size();i++)dp[i][i]=1; for(int i=s.size()-1;i>=0;i--) { for(int j=i+1;j<s.size();j++) { if(s[i]==s[j]) { dp[i][j]=dp[i+1][j-1]+2; } else { dp[i][j]=max(dp[i][j-1],dp[i+1][j]); } } } return dp[0][s.size()-1]; } }; 总结
同理上题但是,在判断回文子串的题目中,关键逻辑就是看s[i]与s[j]是否相同。
如果s[i]与s[j]相同,那么dp[i][j] = dp[i + 1][j - 1] + 2;

动态规划总结篇
https://programmercarl.com/%E5%8A%A8%E6%80%81%E8%A7%84%E5%88%92%E6%80%BB%E7%BB%93%E7%AF%87.html
