3200.三角形的最大高度【简单】
题目:
给你两个整数 red 和 blue,分别表示红色球和蓝色球的数量。你需要使用这些球来组成一个三角形,满足第 1 行有 1 个球,第 2 行有 2 个球,第 3 行有 3 个球,依此类推。
每一行的球必须是 相同 颜色,且相邻行的颜色必须 不同。
返回可以实现的三角形的 最大 高度。
示例 1:
输入: red = 2, blue = 4
输出: 3
解释:
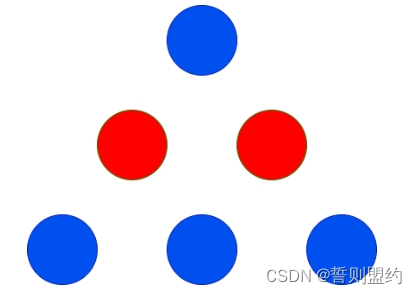
上图显示了唯一可能的排列方式。
示例 2:
输入: red = 2, blue = 1
输出: 2
解释:
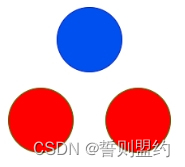
上图显示了唯一可能的排列方式。
示例 3:
输入: red = 1, blue = 1
输出: 1
示例 4:
输入: red = 10, blue = 1
输出: 2
解释:
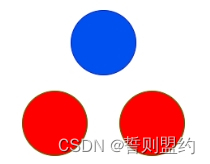
上图显示了唯一可能的排列方式。
提示:
1 <= red, blue <= 100
分析问题:
这里需要分情况讨论:
- 奇排是蓝球:那么蓝色第一层初始值为1,往下每层个数依次+2,需要蓝色球的个数每次都加本层的个数。模拟过程,求出蓝色球的数量一共够放多少层。同样的办法求出红色球能放的总层数。两者去min值*2就是初定的层数,但是需要注意的是,这里当蓝色球层数大于红色球层数时,总层数是需要+1的,因为蓝球开始又以蓝球结束。总层数+1即为结果。
- 奇排是红球:同样的道理,设红球的初始值为1,求出层数即可。
最后返回二者的max值即为答案。
这道题容易产生一种错误的思路:数量多的球就应该放第一排,或者数量少的球就应该放第一排。这种思路是错的,可以自行验证。
代码实现:
class Solution: def maxHeightOfTriangle(self, red: int, blue: int) -> int: b,r=1,0 h1,h2=1,0 s1,s2=1,0 while s1+h1+2<=blue: h1+=2 b+=1 s1+=h1 while s2+h2+2<=red: h2+=2 r+=1 s2+=h2 a=min(b,r)*2 if b-r>=1: a+=1 r,b=1,0 h1,h2=1,0 s1,s2=1,0 while s1+h1+2<=red: h1+=2 r+=1 s1+=h1 while s2+(h2+2)<=blue: h2+=2 b+=1 s2+=h2 k=min(b,r)*2 if r-b>=1: k+=1 return max(a,k)
3201.找出有效子序列的最大长度I【中等】
题目:
给你一个整数数组 nums。
nums 的子序列 sub 的长度为 x ,如果其满足以下条件,则称其为 有效子序列:
(sub[0] + sub[1]) % 2 == (sub[1] + sub[2]) % 2 == ... == (sub[x - 2] + sub[x - 1]) % 2
返回 nums 的 最长的有效子序列 的长度。
一个 子序列 指的是从原数组中删除一些元素(也可以不删除任何元素),剩余元素保持原来顺序组成的新数组。
示例 1:
输入: nums = [1,2,3,4]
输出: 4
解释:
最长的有效子序列是 [1, 2, 3, 4]。
示例 2:
输入: nums = [1,2,1,1,2,1,2]
输出: 6
解释:
最长的有效子序列是 [1, 2, 1, 2, 1, 2]。
示例 3:
输入: nums = [1,3]
输出: 2
解释:
最长的有效子序列是 [1, 3]。
提示:
2 <= nums.length <= 2 * 10**51 <= nums[i] <= 10**7
分析问题:
这个题是下面3202题的一种简单的情况,直接看下面一题的题解。
代码实现:
class Solution: def maximumLength(self, nums: List[int]) -> int: k=2 f = [[0]*k for i in range(k)] for x in nums: x%=k for y in range(k): f[y][x]=f[x][y]+1 return max(map(max,f)) 
3202.找出有效子序列的最大长度II【中等】
题目:
给你一个整数数组 nums 和一个 正 整数 k 。
nums 的一个
子序列
sub 的长度为 x ,如果其满足以下条件,则称其为 有效子序列 :
(sub[0] + sub[1]) % k == (sub[1] + sub[2]) % k == ... == (sub[x - 2] + sub[x - 1]) % k
返回 nums 的 最长有效子序列 的长度。
示例 1:
输入:nums = [1,2,3,4,5], k = 2
输出:5
解释:
最长有效子序列是 [1, 2, 3, 4, 5] 。
示例 2:
输入:nums = [1,4,2,3,1,4], k = 3
输出:4
解释:
最长有效子序列是 [1, 4, 1, 4] 。
提示:
2 <= nums.length <= 10**31 <= nums[i] <= 10**71 <= k <= 10**3
分析问题:
这里的T3和T2是一个道理,只不过这里的k值可以是任意一个值。分析问题,看透问题的本质。其实这道题给的数组的原本的值并没用,我们需要的是他们各自对k取模之后的值,因为我们要比较的是他们的余数[0,k-1];
对他们各自取模后,可以发现有效子序列的前两个值和后面第三个第四个值就是一个以2为周期的长度为2的数组。也就是说整个有效子序列里面奇数项是同一个数,偶数项是同一个数。奇数项还有可能等于偶数项。
那么知道了这一点,我们用x遍历原数组nums,用y遍历0-k-1就可以可以得到一个递推关系式:f[y][x]=f[x][y]+1,因为以 3 2 结尾的话前面一个数一定是2,那么意思就是说 3 前面是以2 3 结尾的。所以f[3][2]=f[2][3]+1。
代码实现:
class Solution: def maximumLength(self, nums: List[int],k:int) -> int: f = [[0]*k for i in range(k)] for x in nums: x%=k for y in range(k): f[y][x]=f[x][y]+1 return max(map(max,f))
总结:
T3代码详解:
- 创建了一个二维列表
f,大小为kxk,并初始化为全0。 - 遍历
nums列表中的每个元素x,将其对k取模的结果作为新的x。 - 然后遍历
k个值作为y,将f[y][x]的值设置为f[x][y] + 1。 - 最后,使用
max(map(max, f))找出f中所有子列表中的最大值中的最大值,并将其作为结果返回。
考点:
- 对列表的操作和遍历。
- 二维列表的创建和使用。
map()函数和max()函数的应用。
收获:
- 加深了对列表操作和遍历的理解,包括如何创建和修改二维列表。
- 熟悉了
map()函数和max()函数的结合使用,以找出复杂数据结构中的最大值。 - 提高了通过代码解决数学问题的能力,例如通过取模运算和二维列表来处理数据之间的关系。