💎所属专栏:数据结构与算法学习
💎 欢迎大家互三:2的n次方_

🍁1. 树形结构的介绍
树是一种非线性的数据结构,它是由n(n>=0)个有限结点组成一个具有层次关系的集合。把它叫做树是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。
以下是树的一些基本术语
节点的度:一个节点含有子树的个数
树的度:一棵树中所有节点度的最大值
叶子节点(终端节点):度为0的节点
双亲节点(父节点):一个节点的直接前驱节点
孩子节点(子节点):一个节点(除了根节点)的直接后继节点
根节点:没有双亲节点的节点
🍁2. 二叉树的介绍
二叉树是每个节点最多有两个子树的树结构,通常称为左子树和右子树,正如名字一样,每一个节点最多有两个子树。
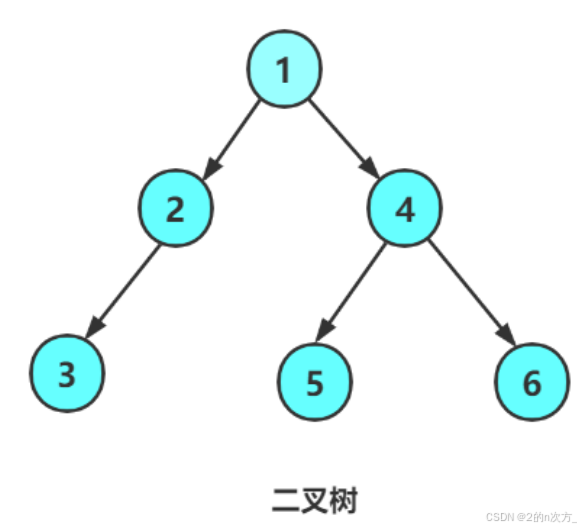
🍁2.1 二叉树的类别
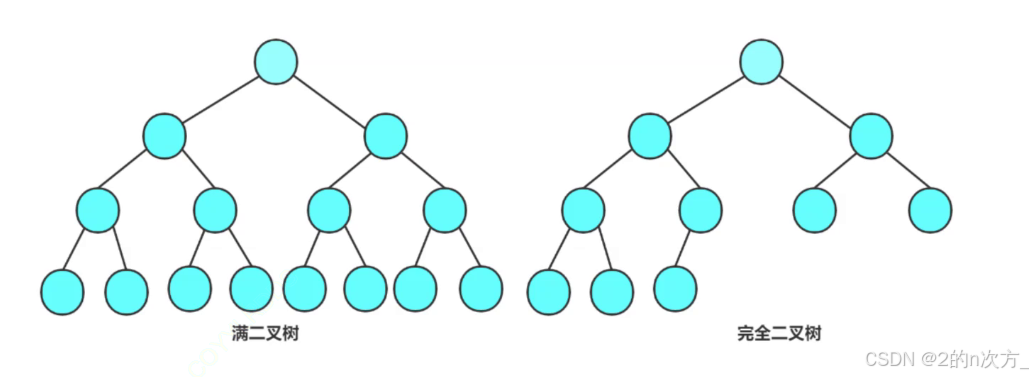
二叉树是树形结构中最重要的一种类型,它有多种特殊形态,如:
- 完全二叉树:除了最后一层外,每一层都被完全填满,并且所有节点都尽可能地向左对齐。
- 满二叉树:除了叶子节点外,每个节点都有两个子节点。
- 平衡二叉树(如AVL树、红黑树):任何节点的两个子树的高度最大差别为一。
- 搜索二叉树(BST):左子树上所有节点的值均小于它的根节点的值,右子树上所有节点的值均大于它的根节点的值。
🍁2.2 二叉树的基本性质
对于任意一棵二叉树,深度为 k 的二叉树,最多有 2的k次方 - 1 个节点。
在任何一棵二叉树中,如果度为2的节点数为 n₂,叶节点数为 n₀,则有关系式 n₀=n₂+1。
任意一棵包含 n 个节点的二叉树的高度至少为 log₂(n+1)(即完全二叉树的高度),最多为 n(即所有节点构成一个链表)。
在具有2 n 个节点的完全二叉树中,叶子节点的个数为 n,2n - 1个节点的完全二叉树中,叶子节点的个数为 n
🍁 2.3 二叉树的存储
二叉树可以通过链式存储和顺序存储的方式存储,这一节主要介绍链式存储
链式存储方式使用节点(Node)对象来表示二叉树的结构。每个节点包含数据部分和两个指针,分别指向其左子节点和右子节点。
例如使用孩子兄弟表示法存储树的效果如下图所示:
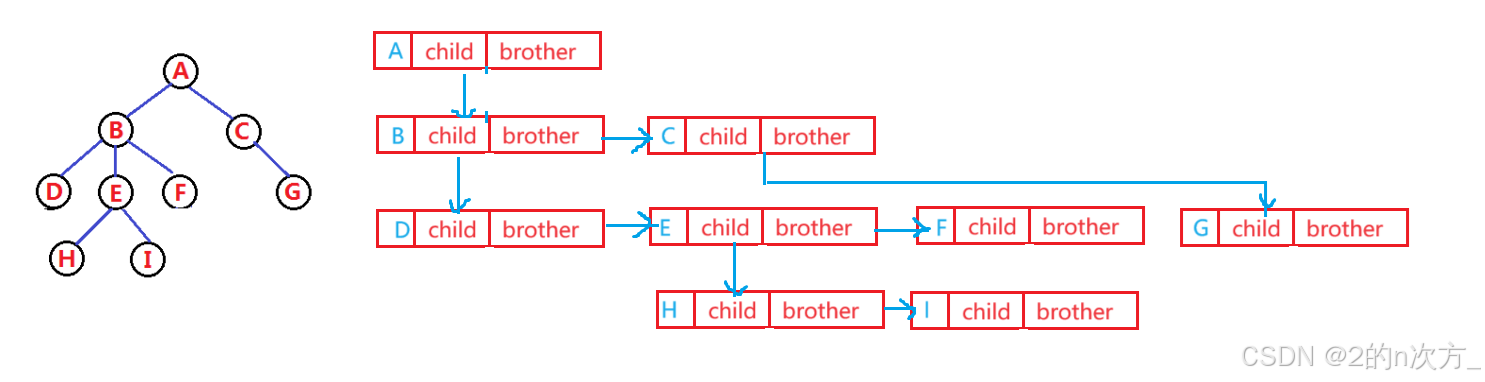
🍁3. 二叉树的实现
class TreeNode { int val; TreeNode left;//左孩子 TreeNode right;//右孩子 TreeNode(int x) { val = x; } } 🍁3.1 二叉树的遍历
树的遍历是树的基本操作之一,常见的遍历方式有:
- 前序遍历:先访问根节点,然后遍历左子树,最后遍历右子树。
- 中序遍历:在二叉搜索树中,先遍历左子树,然后访问根节点,最后遍历右子树。
- 后序遍历:先遍历左子树,然后遍历右子树,最后访问根节点。
- 层序遍历:按从上到下、从左到右的顺序访问树中的每个节点
🍁3.1.1 先序,中序,后序遍历
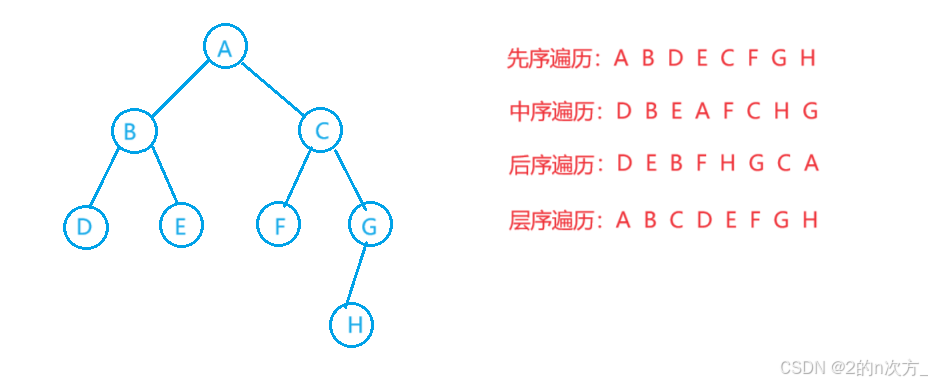
//先序遍历,根左右 public void preOrder(TreeNode root){ if(root == null) return; System.out.print(root.val + " "); preOrder(root.left); preOrder(root.right); } //中序遍历,左根右 public void inOrder(TreeNode root){ if(root == null) return; inOrder(root.left); System.out.print(root.val + " "); inOrder(root.right); } //后序遍历,左右根 public void postOrder(TreeNode root){ if(root == null) return; postOrder(root.left); postOrder(root.right); System.out.print(root.val + " "); }🍁3.1.2 层序遍历
层序遍历的实现需要借助队列来实现,由于队列先进先出的特性,可以依次把头结点,左孩子和右孩子依次入队,接着出队打印,就可以实现层序遍历的效果
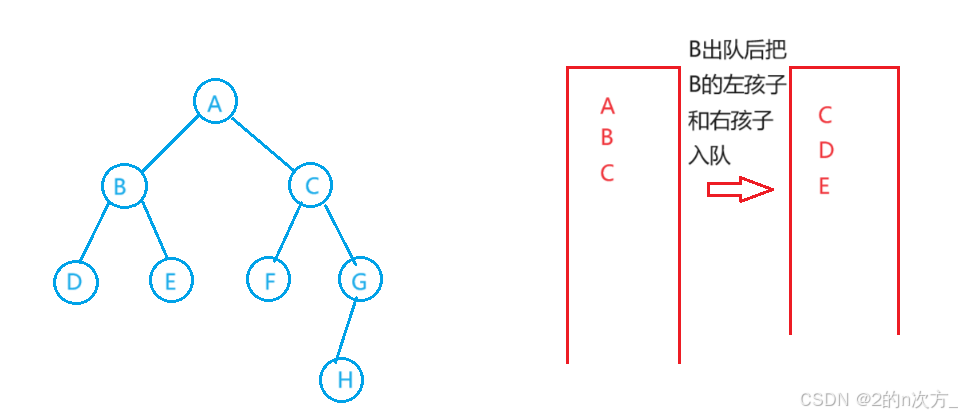
public void levelOrder(TreeNode root) { if (root == null) return; Queue<TreeNode> q = new LinkedList<>(); TreeNode cur = root; q.offer(root); while (!q.isEmpty()) { cur = q.poll(); System.out.print(cur.val + " "); if (cur.left != null) q.offer(cur.left); if (cur.right != null) q.offer(cur.right); } }可以试一下这道力扣上的题
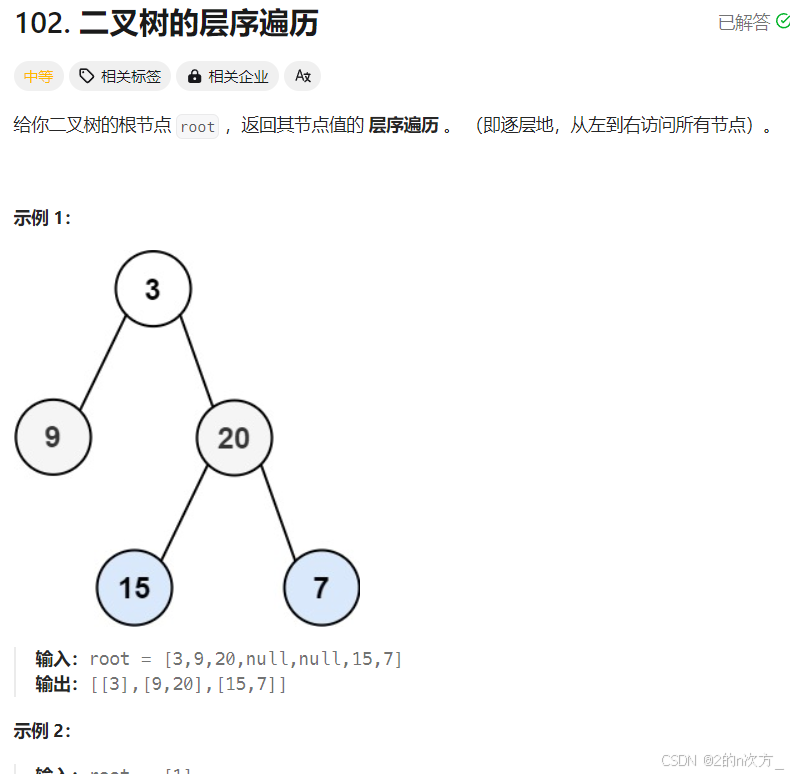
这道题对返回值有了要求,其它的还是正常的层序遍历,答案的形式就是每一层作为一个数组,最终的答案以一个二维顺序表的形式返回
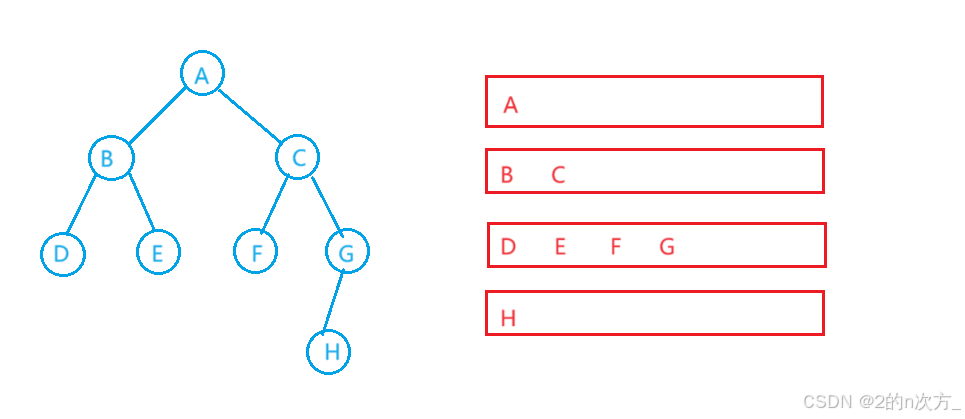
只需要每次入队时计算一下当前队列的元素,把当前层的元素都出队,每次入队的元素也都是下一层的元素
class Solution { public List<List<Integer>> levelOrder(TreeNode root) { List<List<Integer>> res = new ArrayList<>(); if (root == null) return res; Queue<TreeNode> q = new LinkedList<>(); TreeNode cur = root; q.offer(root); while (!q.isEmpty()) { List<Integer> list = new ArrayList<>(); int size = q.size(); //当这一层的元素都出队后,下一层的元素也都能入队 while (size!=0) { cur = q.poll(); list.add(cur.val); if (cur.left != null) q.offer(cur.left); if (cur.right != null) q.offer(cur.right); size--; } //添加每层的答案 res.add(list); } return res; } }🍁3.2 size()
求节点数
这里给出遍历和子问题两种思想进行实现
通过前序遍历的方法,通过计数的方式得到二叉树的节点数,分解子问题就是一棵二叉树的每个分支又可以看作一棵二叉树,整个二叉树的节点数就是左子树加上右子树再加上根节点数,根结点数就是1
public static int sizeNode = 0; //遍历思想 public int size(TreeNode root) { if (root == null) return 0; sizeNode++; size(root.left); size(root.right); return sizeNode; } //子问题思想 public int size2(TreeNode root) { if (root == null) return 0; return size2(root.left) + size2(root.right) + 1; }🍁3.3 getLeafNodeCount(TreeNode root)
求叶子节点数
依然可以使用两种方法,通过遍历找出叶子节点,分解子问题就是左子树的叶子节点加上右子树的叶子节点等于二叉树的叶子节点,因为根节点肯定不是叶子节点
public static int leafSize = 0; public int getLeafNodeCount(TreeNode root) { if (root == null) return 0; //判断叶子节点 if (root.left == null && root.right == null) { leafSize++; } getLeafNodeCount(root.left); getLeafNodeCount(root.right); return leafSize; } public int getLeafNodeCount2(TreeNode root) { if (root == null) return 0; if (root.left == null && root.right == null) return 1; return getLeafNodeCount2(root.left) + getLeafNodeCount2(root.right); }🍁3.4 getKLeveLNodeCount(TreeNode root, int k)
获取第 k 层的节点数
public int getKLeveLNodeCount(TreeNode root, int k) { if (root == null) { return 0; } if (k == 1) return 1; return getKLeveLNodeCount(root.left, k - 1) + getKLeveLNodeCount(root.right, k - 1); }🍁3.5 getHeight(TreeNode root)
获取二叉树的高度
还是通过递归来实现,二叉树的高度其实也就是左子树和右子树的最大值,再加上根节点的一层,就是整棵树的高度
public int getHeight(TreeNode root) { if (root == null) return 0; return Math.max(getHeight(root.left),getHeight(root.right)) + 1; }🍁3.6 findVal(TreeNode root,char val)
检测val是否存在二叉树中
只需要依次判断根节点,左子树,右子树,通过分解子问题,左子树又可以分为根节点,左子树右子树,依次达到遍历整棵树的效果,判断val是否存在
public TreeNode findVal(TreeNode root,char val){ if(root == null) return null; if(root.val == val) return root; TreeNode t1 = findVal(root.left,val); if(t1 != null) return t1; TreeNode t2 = findVal(root.right,val); if(t2!= null) return t2; return null; }🍁3.7 isCompleteTree(TreeNode root)
判断是否为完全二叉树
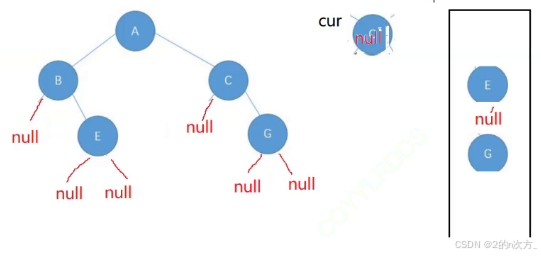
当遍历二叉树时,如果遍历到的cur节点此时为null,并且此时队列中剩余元素也都是null,那么就是完全二叉树
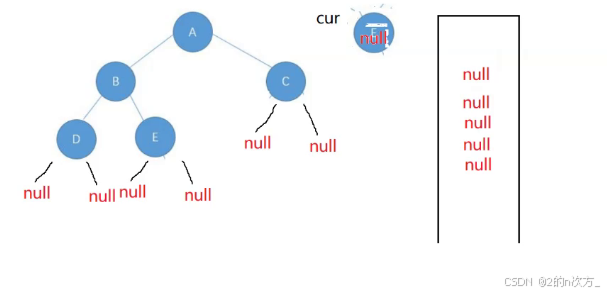
反之,如果剩余元素有不为null的,那么就不是完全二叉树,例如下面的图中,当遍历到B的左孩子为null时,此时队列中还有E,G等不为null的元素
public boolean isCompleteTree(TreeNode root) { if (root == null) return false; Queue<TreeNode> q = new LinkedList<>(); q.offer(root); //找到cur为空时的位置 while (!q.isEmpty()) { TreeNode cur = q.poll(); if (cur != null) { q.offer(cur.left); q.offer(cur.right); }else { break; } } //继续判断剩余队列是否有不为null的元素 while(!q.isEmpty()){ if(q.peek()!=null) return false; q.poll(); } return true; }

