目录
一、前言
经常刷算法题的朋友,肯定会经常看到题目中提到 字典序 这样的字眼,或者需要我们通过字典序来解题,由于之前对字典序了解的不太清楚,导致做题的时候总会卡住,所以收集了一些资料来详解字典序。
二、什么是字典序 ?
✨字典序概念
字典序(dictionary order),又称 字母序(alphabetical order),含义是表示英文单词在字典中的先后顺序,在计算机领域中扩展成两个任意字符串的大小关系。
举例:
在字典中,单词是按照首字母在字母表中的顺序进行排列的,比如 alpha 在 beta 之前。而第一个字母相同时,会去比较两个单词的第二个字母在字母表中的顺序,比如 account 在 advanced 之前,以此类推。下列单词就是按照字典序进行排列的:
as aster astrolabe astronomy astrophysics at ataman attack baa✨深度理解字典序
- 在学习 字符串string的时候,我们肯定接触过两个字符串之间的比较,比如”abc“ < “acb” < “acbd”, 其规则是先比较第一个字母,如果不相等,就直接得到结果,如果相等,就比较下一个字母。
- 如果两个字符串的长度不相等,但是长的那个字符串包含了短的那个,那长的那个字符串更大(比如"acb" < “acbd”)
- 在我们进行比较之前,有一个默认的排序规则,就是‘a' < 'b' < 'c' < ... < 'z'
举例:
对数字 【1,2,3,4,5,6,7,8,9,10,11,12,13】 按照字典序排列: 结果为 :【1,10,11,12,13,2,3,4,5,6,7,8,9】 总结:
对于两个不同的字符串,从左到右逐个比较它们的字符,
- 如果在某个位置上它们的字符不同,则将它们按照该位置上的字符的字母顺序进行排序,即较小的字符排在前面,较大的字符排在后面。
- 如果一直比较到其中一个字符串结束,则较短的字符串排在前面;
- 如果两个字符串完全相同,则它们的字典序相同。可以将它们看作是按照字母表的顺序进行排列的。
✨字典序排序的重要性和应用场景
- 数据库索引:在数据库中,使用字典序排序可以加快查询速度。例如,对存储了字符串数据的列进行字典序排序,可以使得数据库在执行字符串比较操作时更高效。
- 字符串比较:在字符串比较场景中,字典序排序能够方便地判断两个字符串的大小关系。例如,在编程中,可以使用字典序排序来实现字符串的字母顺序排序、查找最大/最小字符串等操作。
- 文件系统排序:文件系统通常使用字典序排序来显示文件和目录的顺序。这样可以使得用户在文件浏览器中更容易找到特定的文件或目录。
三、常考面试题
通过上面的讲解,相信大家应该对 字典序 有了一个基础的了解,想要深刻的理解它,还是需要通过题目来理解。
✨ 下一个排列

题目分析:
- 说实话刚看题目我看了半天不知道在说什么,看到评论里面提到字典序算法才知道题意。我们拿题目中的例子
1,2,3 ------> 1,3,2来说明:
- 首先本题讨论的范围是数字,数字中有一个规则,就是’0‘ < '1' < '2' < ... < '9',这与上面的a~z是一样的
- 然后就是1,2,3这三个数字,我们能够形成6种不同的组合,即123 < 132 < 213 < 231 < 312 < 321。
- OK,如果你看懂前面两点,本题已经完成了。我们要做的就是找到当前数 123 在第二点的六种排列中间的下一个位置是什么,即 132,那么 132 就是答案
- 如果要找的数字位于排列组合的最后一个一位,即 321,那么按照题目的第二行,我们就返回最小值 123.
上面从直觉上理解了什么是字典序算法,下面说下怎么转化成程序算法。
何时无解
首先考虑无解情况,即上面所说的321,这种情况带入字典序算法是无解的,而321这种情况,如果我们单独拆分成3,2,1三个数字,其实是一个降序的过程:
- 因此如果当前排列是降序的,则字典序算法无解
- 换而言之,如果不存在后一个数比前一个数大(2<3,1<2),字典序算法无解
- 比如下图中的54321抽象出来的五个点,不存在后一个点大于前一个点,因此无解。

有解的情况
下面我们拿51432这个例子,来一步步说明如何通过字典序算法得到 52134 这个答案的

1. 从右往左找,找到第一个右边比左边大的数
- 首先我们从最右边的2开始,因为2 < 3,因此跳过。然后3 < 4,再跳过。然后发现4 > 1,OK,第一步完成。
- 然后我们在上图中用黄色点标记这两个数,即1 和 4
2. 找到断点右边所有数中最小的一个 (包括断点)
- 如果我们直接交换两个黄点,得到 54132,虽然也比 51432 大,但是它不符合字典序算法中的规则,因为这两个数中间还夹杂着别的数51432 < 52134 < 52143 < 52314 < ...... < 54132,字典序算法中必须满足两个数之间不能夹杂其他数才行。
- 而根据上面列举的,我们知道 52134 才是我i们想要的答案,它的特点就是我们需要把 1 换成2,而不是 4。
- 而 2 实际上就是4,3,2中间的最小值,因此这一步我们要做的就是找到左边黄点(1)右边的所有数(4,3,2)中间最小的一个数(2),然后我们用 红点标记下来。
- 之所以要交换1和2,而不是1和3或者1和4,是因为我们现在是要把千位的1换成一个更大中的最小的情况,因此要选2.
3.交换左边的黄点和红点
- 上面我们找到了红点(2),因此这一步我们需要讲红点跟左边的黄点(2)进行交换,得到52431
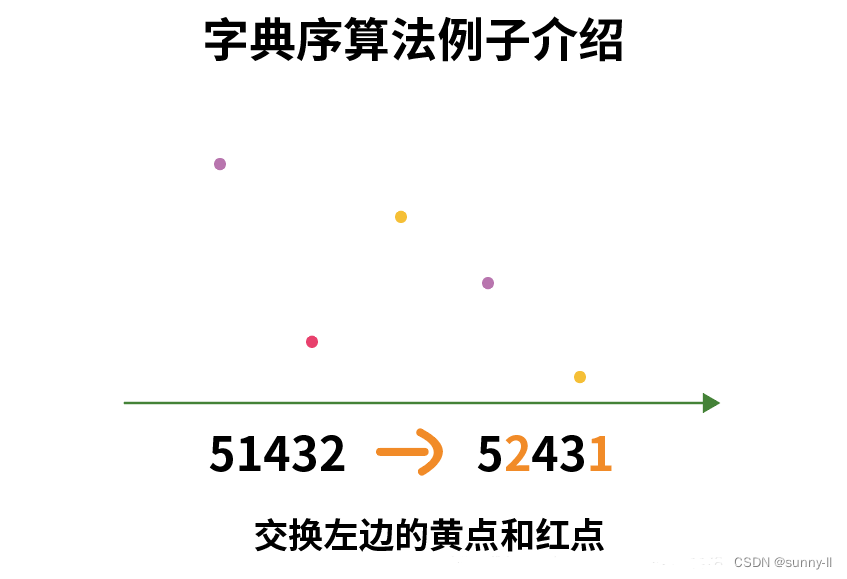
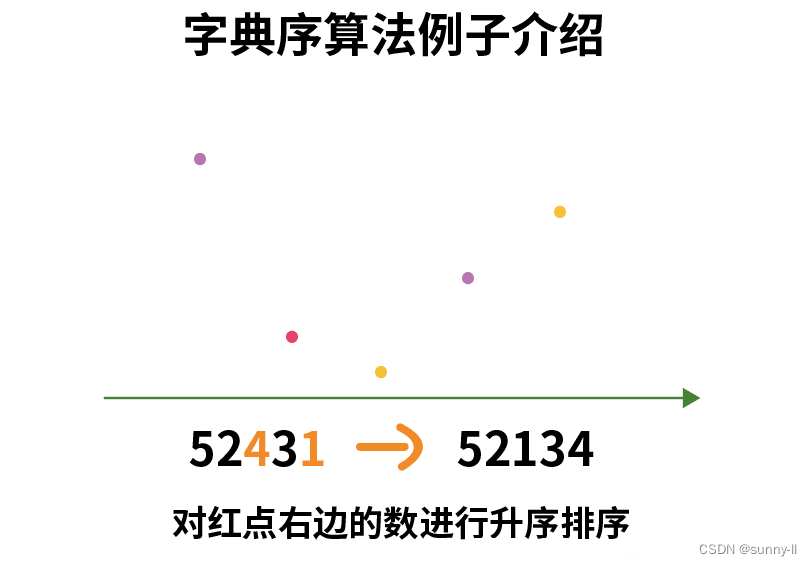
4. 对红点右边的数进行升序排序
- 此时,我们交换了千位的1和个位2,变成了52431.但是距离我们的最终答案52134还差了一步,52134 < 52143 < 52314 < 52341 < 52413 < 52431,👈由这个规则可以看到我们的千位和万位已经相同了,但是个十百位还未相同了,而因为我们要找的答案要尽可能小,因此需要进行升序排序,得到52134,大功告成!
代码:
class Solution { public: void nextPermutation(vector<int>& nums) { // 用于判断是否无解 -- 开始默认无解 bool flag = 0; for(int i = nums.size()-1;i>0;i--) { if(nums[i]>nums[i-1]) { // 有解 flag = 1; // 初始化最小值 为右边断点 int min = nums[i],idx = i; // 向后找最小值 for(int j = i+1;j<nums.size();j++) { if(nums[j]<min && nums[j] > nums[i-1]) { // 更新最小值 min = nums[j]; // 存储小标,便于后续交换 idx = j; } } // 将右边最小值 和 左边最小值交换 (左右区分,以断点为界线) nums[i - 1]^= nums[idx]; nums[idx]^= nums[i - 1]; // 小技巧 位运算 不用第三个参数来交换两个数 nums[i - 1]^= nums[idx]; // 将左边的数据 包括断点进行升序排序 sort(nums.begin()+i,nums.end()); break; } } // 确定误解 将动态数组全部进行 升序排序 if(flag == 0) { sort(nums.begin(),nums.end()); } } };✨ 字典数排序

class Solution { public: static bool cmp(int a,int b) { string s1 = to_string(a); string s2 = to_string(b); // 字典升序 return s1<s2; } vector<int> lexicalOrder(int n) { vector<int> res; while(n!=0) { res.push_back(n); n--; } sort(res.begin(),res.end(),cmp); return res; } };✨ 字典序最小回文串

题目分析:
对于两个中心对称的字母 x = s[i] 和 y = s[ n - 1 - i ] , 如果 x != y ,那么只需要修改一次,就可以让这两个字母相同:把 x 改成 y 或者 把 y 改成 x。
- 如果 x > y , 那么把 x 修改成 y 更好 , 这样字典序更小
- 如果 x < y , 那么把 y 修改成 x 更好 , 这样字典序更小
代码:
class Solution { public: string makeSmallestPalindrome(string s) { // 双指针 分别指向 头部和尾部 int begin = 0,end = s.size()-1; while(begin<end) { if(s[begin]!=s[end]) { s[begin] = s[end] = min(s[begin],s[end]); } begin++; end--; } return s; } };四、共勉
以下就是我对 字典序 的理解,如果有不懂和发现问题的小伙伴,请在评论区说出来哦,同时我还会继续更新对 C++ 的更新,请持续关注我哦!!!

