阅读量:0
由于最近要考试,好久没有发博客了,非常抱歉大家对我的支持。之后我会不断更新博客,继续创作出高质量的文章,希望能帮到大家!
文章目录
一、归并排序基本思想
归并排序(MERGE-SORT)是建立在归并操作上的一种有效的排序算法,该算法是采用分治法,即分解和合并。先使每个子序列有序,再使子序列段间有序,最后合并成一个有序数组。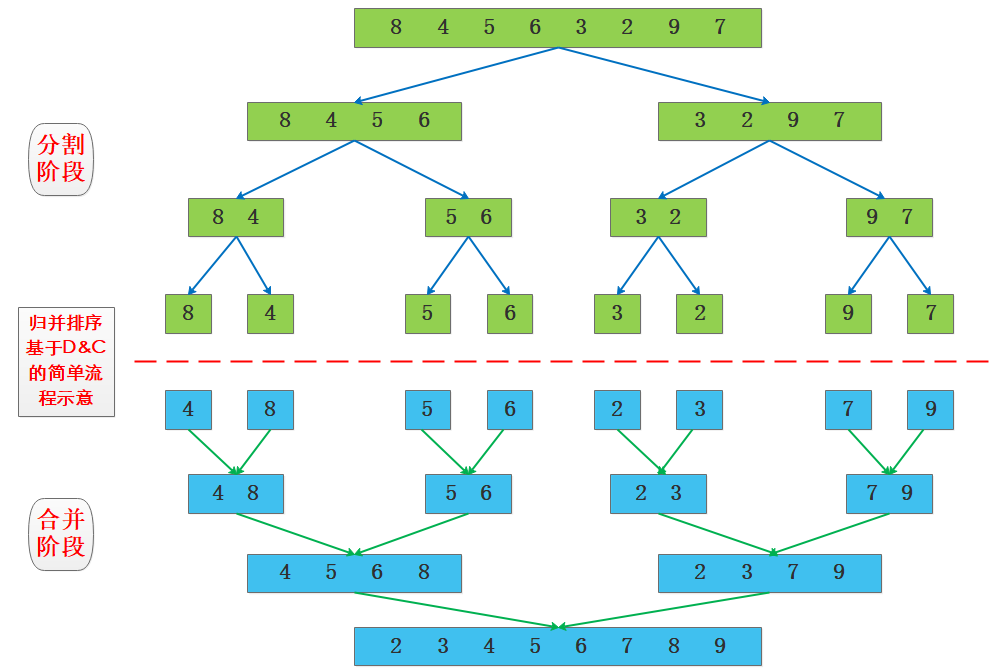
二、递归实现
- 基本思路:
① 申请一个空间tmp,大小为两个已经排好序列之和,该空间用来存放合并后的序列。
② 设定两个下标,分别指向两段已排好序的起始位置。
③ 比较两个下标所指向的元素大小,选择较小的元素放入到合并空间,并且移动指针指向下一位置。
④ 不断重复步骤③,直到当某一指针到达序列尾部。
⑤ 然后将另一序列剩下的所有元素直接插入到合并序列的尾端。 - 代码实现:
//归并排序递归 void _MergeSort(int* a, int* tmp, int begin, int end) { //只有一个元素或不存在这样的区间时 if (begin >= end) { return; } //分成两段区间,分别有序时在进行归并 int mid = (begin + end) / 2; _MergeSort(a, tmp, begin, mid); _MergeSort(a, tmp, mid + 1, end); //第一个数组的两端 int begin1 = begin, end1 = mid; //第二个数组的两端 int begin2 = mid + 1, end2 = end; //由于两段数组都是从begin开始,因此将begin给i确保其在相同的区间上 int i = begin; while (begin1 <= end1 && begin2 <= end2) { if (a[begin1] < a[begin2]) { tmp[i++] = a[begin1++]; } else { tmp[i++] = a[begin2++]; } } //有一个排完了,剩下的直接放入 while (begin1 <= end1) { tmp[i++] = a[begin1++]; } while (begin2 <= end2) { tmp[i++] = a[begin2++]; } //tmp已经归并成功,将tmp复制会数组a中 memcpy(a + begin, tmp + begin, (end - begin + 1) * sizeof(int)); } void MergeSort(int* a, int n) { assert(a); //创建一个临时数组 int* tmp = (int*)malloc(sizeof(int) * n); if (tmp == NULL) { perror("malloc fail"); return; } _MergeSort(a, tmp, 0, n - 1); free(tmp); tmp = NULL; } 三、非递归实现
非递归实现是一种迭代式的排序算法,它避免了递归所带来的额外开销,通常使用循环的方式来解决。
- 基本思路:
将一个数组通过gap分为几组进行合并,然后让gap每次扩大2倍,但gap < 数组元素个数的大小。 - 越界问题:
我们可以很容易想到代码实现的思路,但难点就在于如何控制每一段区间的边界,从而避免下标越界的问题。
这里有三种可能会出现越界的问题,分别为:
①当第一段区间末尾end1大于或等于该区间元素个数。
②当第二段区间不存在,需要进行修改区间。
解决方法:
①第一种问题我们可以让其直接break。因为其右边没数据存在,因此就算进入循环中剩余的元素也不会发生改变。
②第二种问题,当第二段区间bgein2大于或等于该区间元素个数时,不进入循环,直接break;当第二段区间的结尾end2大于或等于n时,我们只需将end2修改为n-1即可,因为n-1正好为整个数组的边界。 - 代码实现:
注意:
当我们将临时数组tmp拷贝回原数组时:
①起始点为:tmp + i,因为i是每次归并后第一个元素的第一个位置。
②拷贝回去的元素个数:end2 - i + 1。因为end2指向的每次归并后第二组元素的最后一个位置,而i所指向的是每次归并后的第一个元素的第一个位置。
//归并排序的非递归实现 void MergeSortNonR(int* a, int n) { //开辟一个临时数组,来存取排好序的元素 int* tmp = (int*)malloc(sizeof(int) * n); if (tmp == NULL) { perror("malloc fail"); return; } int gap = 1; int i = 0; int j = 0; while (gap < n) { for (i = 0; i < n; i += 2 * gap) { //[i,i+gap-1] [i+gap,i+2*gap-1} int begin1 = i; int end1 = i + gap - 1; int begin2 = i + gap; int end2 = i + 2 * gap - 1; j = i; // 考虑end1 begin2 end2三者分别越界的问题 if (end1 >= n) { break; } else if (begin2 >= n) { break; } else if (end2 >= n) { end2 = n - 1; } while (begin1 <= end1 && begin2 <= end2) { if (a[begin1] < a[begin2]) { tmp[j++] = a[begin1++]; } else { tmp[j++] = a[begin2++]; } } while (begin1 <= end1) { tmp[j++] = a[begin1++]; } while (begin2 <= end2) { tmp[j++] = a[begin2++]; } memcpy(a + i, tmp + i, sizeof(int) * (end2 - i + 1)); } gap *= 2; } free(tmp); tmp = NULL; } 四、效率分析
归并排序的时间复杂度为:O(N * log2N) 因为向下递归的时间复杂度为O(log2N),再遍历一次数组的时间复杂度为O(N)。
归并排序的空间复杂度为:O(N) 需要创建一个辅助数组tmp用来存归并后的序列。
归并排序的稳定性:稳定。根据arr[begin1] <= arr[begin2],我们可以得出相同的元素先排第一组,然后再排第二组的元素,因此相同元素的相对位置不会改变。
