这个算法《算法导论》中并没有提及,很多书和博客说的有点奇怪,所以写本文作为笔记。
关键路径是什么
关键路径的定义非常简单:就是一个图中,权值之和最大的路径就是关键路径。
那么就可以知道关键路径不唯一。
为什么有关键路径
关键路径的来源和拓扑排序是一样的,都是将一项较大的工程划分为多个子工程,然后表示子工程之间的关系的。
关键路径和拓扑排序不同之处在于:
- 拓扑排序强调子工程之间的先后顺序(说依赖关系可能更恰当一些),比如必须做完
a才能做c。 - 关键路径在拓扑排序的基础上,还加入了时间关系。这个时间关系不光是子工程之间的,也包括子工程和整体之间的。
比如必须做完a和b才能做c,做完c和d才能做e,而a需要 3 天,b需要 5 天,c需要 1 天,d需要 4 天。
- 那么整体上来说,
c必须要等五天后才可以开始做,这个 5 天有个术语叫c的最早发生时间,也就是c最快要什么时候开始。d的最早发生时间是0,因为没有前置事件,同理a和b也是 0。d最快可以一开始就做,因为没有前置事件,但是最晚开始的时间,只能推迟一天,不然加上做的 4 天,1+4=5,会导致c做完了,d还没做完,就会耽误e的发生。而这个 1 天的术语叫做最迟发生时间,也就是d最晚要什么时候开始。需要注意这里的时间由于是从
0开始的,等五天后得到的是2+3=5,相当于第六天开始,写算法的时候要注意这点。
- 局部来说,
a可以延期 2 天再开始,d可以延期 1 天,也都不会耽误进度。在关键路径中,这个可以延期的时间也有个术语叫做时间余量。可以看到就是最迟发生时间 - 最早发生时间,或者说结束时间-(最早结束时间-子工程耗时),明白含义之后,公式和变形就很好记了。
当然稍微复杂一些的最迟发生时间就很难简单看出来了,因为前置条件太复杂,所以要有个计算流程,避免人为出错。
如何求得关键路径
求关键路径的方法很多书上说的很难似的,其实很简单。以下图为例:
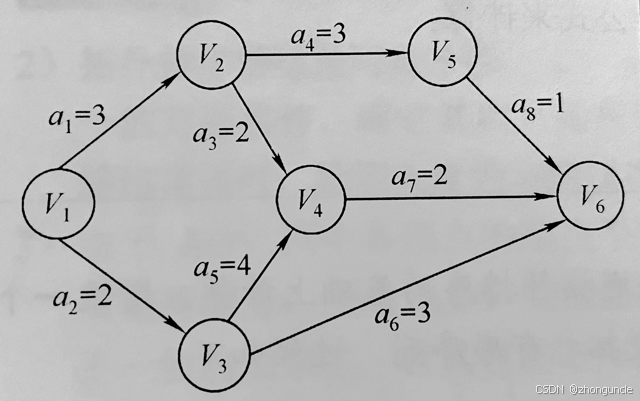
源点(开始的点)选择是V1。
AOE 关键路径图中,顶点是子工程的开始,边是事件。箭头可以理解为时间的发展方向。这与拓扑排序不同。
第一步:求子工程之间的关系和最早发生时间
关键路径的来源和拓扑排序是一样的,第一步当然是先找到子工程之间的依赖关系,在这个过程中,可以顺道加上路径的权值(在上面的例子中,也就是天数)。
那么可以得到一个序列和每个节点的最早开始时间 V e ( i ) V_e(i) Ve(i)。也就是路径权值相加最大值,具体来说,就是多个前驱的时候选最早开始时间+权值最大的一个,刚好与最短路径算法相反:
| V 1 V_1 V1 | V 2 V_2 V2 | V 3 V_3 V3 | V 4 V_4 V4 | V 5 V_5 V5 | V 6 V_6 V6 | |
|---|---|---|---|---|---|---|
| V e ( i ) V_e(i) Ve(i) | 0 | 3 | 2 | 6 | 6 | 8 |
下标
e表示early,早嘛。
第二步:求子工程最迟发生时间(逆拓扑排序)
拓扑排序是先从无前驱的节点开始(没有前置条件),然后删点删边,一次次后得到序列。而逆拓扑排序是从无后继节点开始(不会影响其他节点)。
这里概念听上去就很乱,但是实际上你可以重现画一个图,前驱改后继,后继改前驱(箭头取反),然后从得到的最大值(这里是8)进行拓扑排序和记录时间(加变减),得到的结果一样的,远比书上的方法简单快速,不易出错。
如果你看不到下面的,就按照上面的说法,自己拿草稿纸画一下,立马就懂了。
那么可以得到一个序列和对应的最迟开始时间 V l ( i ) V_l(i) Vl(i)。具体每步就是从尾部开始,每个节点的最迟开始时间 V l ( i ) V_l(i) Vl(i)为上一个节点的最后开始时间 - 前驱的最小权值。
上面得到的最早开始时间序列为:
| V 1 V_1 V1 | V 2 V_2 V2 | V 3 V_3 V3 | V 4 V_4 V4 | V 5 V_5 V5 | V 6 V_6 V6 | |
|---|---|---|---|---|---|---|
| V e ( i ) V_e(i) Ve(i) | 0 | 3 | 2 | 6 | 6 | 8 |
最后一个节点的最迟开始时间和最早开始时间一样:
| V 1 V_1 V1 | V 2 V_2 V2 | V 3 V_3 V3 | V 4 V_4 V4 | V 5 V_5 V5 | V 6 V_6 V6 | |
|---|---|---|---|---|---|---|
| V e ( i ) V_e(i) Ve(i) | 0 | 3 | 2 | 6 | 6 | 8 |
| V l ( i ) V_l(i) Vl(i) | 8 |
V 6 V_6 V6逆拓扑排序消除 V 4 V_4 V4、 V 5 V_5 V5对应的权值为2、1(就一个,不分大小了就)。8减去可得:
| V 1 V_1 V1 | V 2 V_2 V2 | V 3 V_3 V3 | V 4 V_4 V4 | V 5 V_5 V5 | V 6 V_6 V6 | |
|---|---|---|---|---|---|---|
| V e ( i ) V_e(i) Ve(i) | 0 | 3 | 2 | 6 | 6 | 8 |
| V l ( i ) V_l(i) Vl(i) | 6 | 7 | 8 |
然后逆拓扑排序 V 2 V_2 V2、 V 3 V_3 V3,要求节点最晚发生时间-权值最小,那么对应最小权值为2、4(都从 V 4 V_4 V4),6减去这两个值可得:
这里是为了说明,实际上算出来直接选就行了,“最小权值”不需要求出来。
| V 1 V_1 V1 | V 2 V_2 V2 | V 3 V_3 V3 | V 4 V_4 V4 | V 5 V_5 V5 | V 6 V_6 V6 | |
|---|---|---|---|---|---|---|
| V e ( i ) V_e(i) Ve(i) | 0 | 3 | 2 | 6 | 6 | 8 |
| V l ( i ) V_l(i) Vl(i) | 4 | 2 | 6 | 7 | 8 |
最后减去最小后继权值2(从 V 3 V_3 V3),2减去这个值可得:
| V 1 V_1 V1 | V 2 V_2 V2 | V 3 V_3 V3 | V 4 V_4 V4 | V 5 V_5 V5 | V 6 V_6 V6 | |
|---|---|---|---|---|---|---|
| V e ( i ) V_e(i) Ve(i) | 0 | 3 | 2 | 6 | 6 | 8 |
| V l ( i ) V_l(i) Vl(i) | 0 | 4 | 2 | 6 | 7 | 8 |
第三步:作差得到时间余量,为0的就是关键节点,组成关键路径
| V 1 V_1 V1 | V 2 V_2 V2 | V 3 V_3 V3 | V 4 V_4 V4 | V 5 V_5 V5 | V 6 V_6 V6 | |
|---|---|---|---|---|---|---|
| V e ( i ) V_e(i) Ve(i) | 0 | 3 | 2 | 6 | 6 | 8 |
| V l ( i ) V_l(i) Vl(i) | 0 | 4 | 2 | 6 | 7 | 8 |
| V l ( i ) − V e ( i ) V_l(i)-V_e(i) Vl(i)−Ve(i) | 0 | 1 | 0 | 0 | 1 | 0 |
那么关键路径就为: V 1 − > V 3 − > V 4 − > V 6 V_1 -> V_3 -> V_4 -> V_6 V1−>V3−>V4−>V6。很多图的关键路径不能这么算,因为可能有多个路径的权值之和都是最大值,也就是说有多个关键路径,那么就要自己看一下图了,选一个好算的。(也就是下一节的内容)
快速计算
按照上面的方法很烦,每次计算都要算两个序列,我又不是电脑,算那么多很慢的,所以可以直接找最大后继或最小前驱。
以 2019 年 408 的一道题来说:找出下面 AOE 网中,活动 d最早开始时间和最晚开始时间。
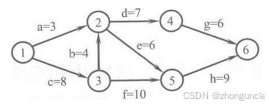
你可以算两个序列,但是那太麻烦了。
开始时间就是前面的节点,也就是2。那就算从1到2之间最大的路径和最长路径减去2到6之间的最小路径。
那么眼一打最早开始时间就是12。
最晚开始时间可能需要算一下1到6的最大路径,算出来是27。然后继续用眼一打,2到6之间的最小路径为13,那么27-13=14。所以最晚开始时间是14。
怕看错,就把每个路径写出来,然后选出最大/最小的一个,有些路径大题就是这么答的。
这个原理是关键路径的定义:权值之和最大的路径就是关键路径。所以关键路径不唯一,我们可以利用这一点选一个好算的路径就行了。
关键路径有何用
我们前文说,关键路径表示的是工程所需的最大时间,那么就可以使用关键路径得知如何改进时间。
如果改进一件事的时间,可以让所有关键路径(也就是最大值)减少,那么改进这件事所需的时间,就可以减少整个工程所需的时间。
希望能帮到有需要的人~
