MATLAB: ode45 求解常微分方程

引入

ode45 是 MATLAB 中用于求解非刚性常微分方程（ODE）的数值方法。它基于 Runge-Kutta 方法，并具有自适应步长调整机制，能够在一定误差控制范围内高效地计算 ODE 的数值解。

下面我们通过这个包含详细注释的代码，一起学习一下这个函数的使用：

使用 ode45 求解非线性常微分方程并绘制数值解与精确解对比图

方程模型

我们考虑以下非线性常微分方程：

$y^{\prime \prime }=-y^{\prime }+\cos (t)-3\sin (t)$

##初始条件

选择初始条件：
$y(0.1)=\cos (0.1)+2\sin (0.1)$
$y^{\prime }(0.1)=-\sin (0.1)+2\cos (0.1)$

使用 ode45 求解 ODE

以下是使用 ode45 求解该方程的 MATLAB 代码，并绘制数值解与精确解的对比图：

% 定义非线性ODE，以下是不同的ODE定义 % ode = @(t, y) [y(2); (f  + y(2).^2 / 2 - 2 * mu .* y(2) ./ (rho .* y(1)) + sig ./ (rho * y(1)) - aB .* y(2).^2 ) ./ (aB * y(1))]; % ode = @(t, y) [y(2); (f + y(2).^2 / 2 - aB .* y(2).^2)];  % 当前使用的ODE定义 ode = @(t, y) [y(2); (-y(2) + cos(t) - 3 * sin(t))];  % 设定初始条件 x0 = 0.1;                      % 初始时间 drealu = @(t) -sin(t) + 2 * cos(t);   % 实际解的导数 realu = @(t) cos(t) + 2 * sin(t);     % 实际解 initial_conditions = [realu(x0); drealu(x0)];  % 初始条件向量  % 定义求解区间 tspan = [x0 10];  % 从初始时间到10的时间区间  % 使用ode45求解ODE [t, y] = ode45(ode, tspan, initial_conditions);  % 绘制数值解 figure; plot(t, y(:, 1), 'o-'); title('numerical solution'); xlabel('time (t)'); ylabel('solution (y(t))'); grid on;  % 绘制实际解 figure; plot(t, realu(t), 'o-'); title('real solution'); xlabel('time (t)'); ylabel('solution (y(t))'); grid on;  

我们画出数值解与精确解对比图：

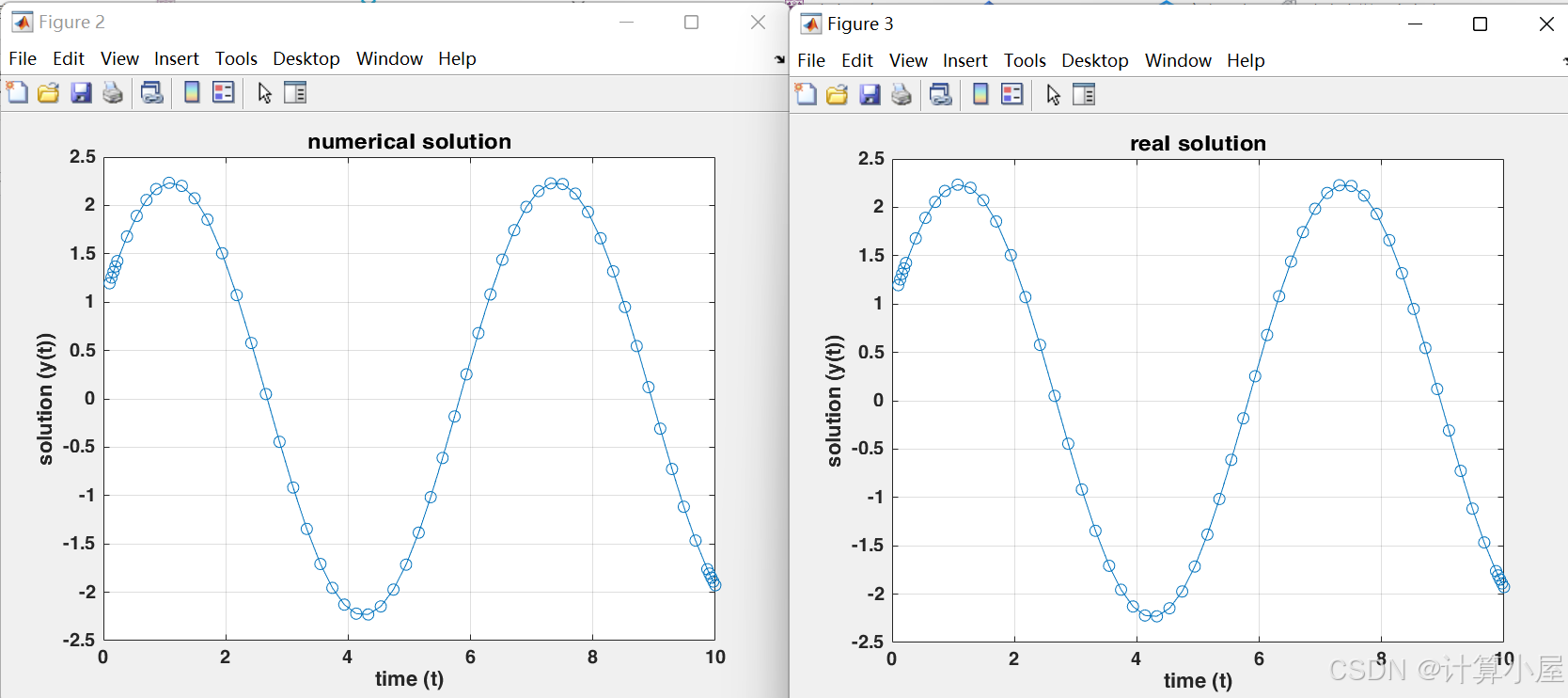
效果不错！

再看一个例子

使用 ode45 求解常微分方程并绘制数值解与精确解对比图

方程模型

我们考虑以下二阶常微分方程：
$y^{\prime \prime }+y=0$

这个方程的精确解为：
$y(t)=A\cos (t)+B\sin (t)$

初始条件

选择初始条件：
$y(0)=1$
$y^{\prime }(0)=0$

根据初始条件，精确解可以写为：
$y(t)=\cos (t)$

使用 ode45 求解 ODE

以下是使用 ode45 求解该方程的 MATLAB 代码，并绘制数值解与精确解的对比图：

% 定义ODE ode = @(t, y) [y(2); -y(1)];  % 初始条件 y0 = [1; 0]; % y(0) = 1, y'(0) = 0  % 定义求解区间 tspan = [0 10];  % 使用ode45求解ODE [t, y] = ode45(ode, tspan, y0);  % 定义精确解 exact_solution = @(t) cos(t);  % 绘制数值解与精确解对比图 figure; plot(t, y(:, 1), 'o-', 'DisplayName', 'Numerical Solution'); % 数值解 hold on; fplot(exact_solution, [0 10], 'r-', 'DisplayName', 'Exact Solution'); % 精确解 title('Comparison of Numerical Solution and Exact Solution'); xlabel('time (t)'); ylabel('solution (y(t))'); legend; grid on; hold off; 

画出数值解与精确解对比图: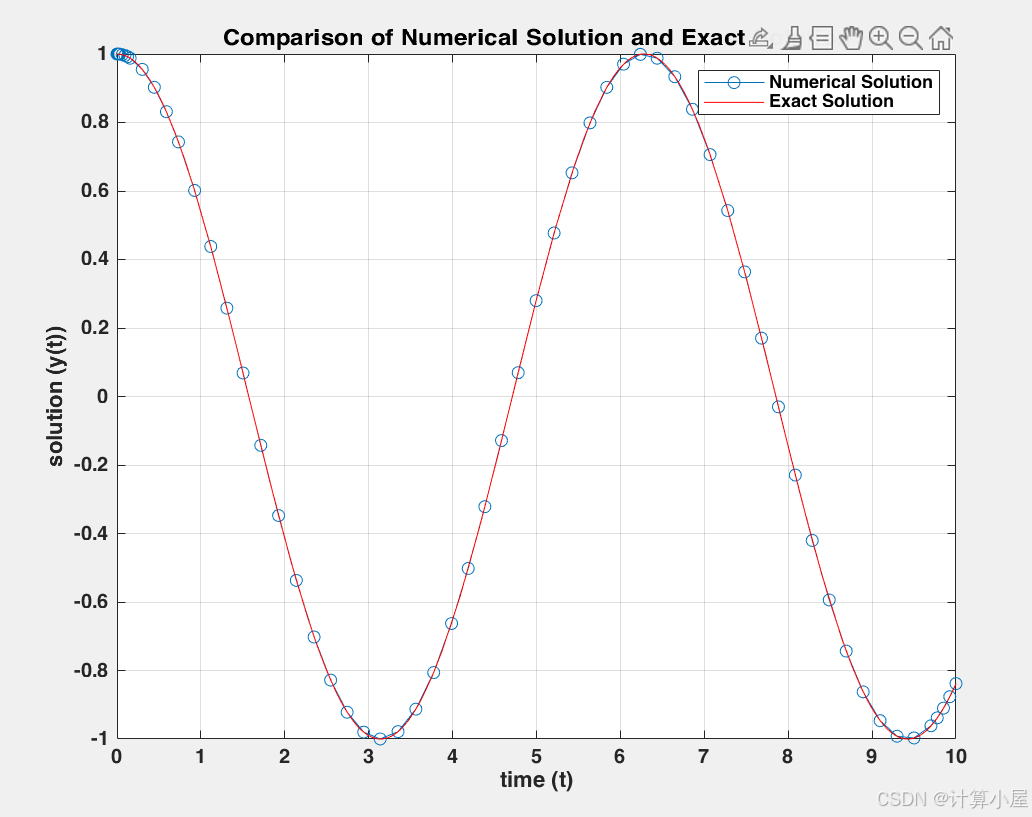

Good!