OpenCV 图像预处理—图像金字塔

文章目录

• • 相关概念
  • • 高斯金字塔
    • 拉普拉斯金字塔
    • 应用
  • 构建高斯金字塔为什么要对当前层进行模糊？
  • • 1. 平滑处理
    • 2. 减少混叠（Aliasing）
    • 3. 多尺度表示
    • 4. 图像降采样
  • 举个栗子
  • • 创建高斯金字塔和拉普拉斯金字塔，并用拉普拉斯金字塔恢复图像

相关概念

高斯金字塔（Gaussian Pyramid）和拉普拉斯金字塔（Laplacian Pyramid）是图像处理中的两种多尺度表示方法，用于图像的分层处理和分析。

高斯金字塔

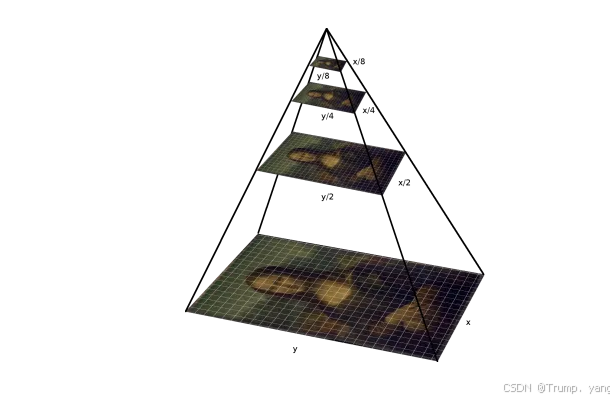
高斯金字塔是一系列按分辨率逐层降低的图像集合，每层图像通过对上一层图像进行高斯模糊和下采样得到。具体步骤如下：

1. 高斯模糊：对图像进行高斯模糊处理，减少高频成分。
2. 下采样：将模糊处理后的图像按一定比例缩小（通常为2）。

这样逐层处理，直到图像变得非常小。高斯金字塔用于图像的多尺度分析，例如图像金字塔法则在图像压缩、特征提取等领域的应用。

构建高斯金字塔的步骤：

1. 从原始图像开始，作为金字塔的最底层。
2. 对当前层图像进行高斯模糊。
3. 对模糊后的图像进行下采样，得到下一层图像。
4. 重复步骤2和步骤3，直到达到预定的层数或图像尺寸小于一定阈值。

拉普拉斯金字塔

拉普拉斯金字塔是高斯金字塔的一种变体，通过记录每层图像与其上层图像之间的差异来构建。具体步骤如下：

1. 高斯金字塔：首先构建高斯金字塔。
2. 图像差异：计算高斯金字塔中每层图像与上层图像的差异。具体来说，对高斯金字塔中的每一层图像进行上采样，并减去相应的上一层图像，得到当前层的拉普拉斯金字塔图像。

拉普拉斯金字塔常用于图像压缩和图像融合等领域，因为它能够有效地表示图像的细节信息。

构建拉普拉斯金字塔的步骤：

1. 构建高斯金字塔。
2. 对高斯金字塔的每一层图像进行上采样。
3. 计算上采样图像与其上层图像的差异，得到当前层的拉普拉斯金字塔图像。
4. 重复步骤2和步骤3，直到达到金字塔顶层。

应用

• 图像压缩：拉普拉斯金字塔可以用于图像压缩，因为它可以有效地表示图像的边缘和细节信息。
• 图像融合：在多分辨率图像融合中，拉普拉斯金字塔可以用于将不同分辨率的图像融合在一起，保留更多的细节信息。
• 图像增强：通过高斯金字塔，可以对图像进行多尺度的平滑处理，有助于去噪和图像增强。

这两种金字塔结构在图像处理和计算机视觉领域都有着广泛的应用。

构建高斯金字塔为什么要对当前层进行模糊？

构建高斯金字塔时对当前层进行高斯模糊（Gaussian Blur）有几个重要的原因：

1. 平滑处理

高斯模糊是对图像进行平滑处理，减少高频噪声和细节。这种平滑处理能够避免在下采样时出现锯齿效应（aliasing），使得下采样后的图像更加平滑和自然。

2. 减少混叠（Aliasing）

混叠效应是指在图像下采样过程中，高频分量折叠回低频分量，导致图像失真。高斯模糊通过平滑处理去除高频分量，减少了混叠效应，使得下采样后的图像更能真实地反映原图像的特征。

3. 多尺度表示

高斯金字塔的构建旨在获得图像的多尺度表示。通过对图像进行高斯模糊并逐层下采样，可以生成一系列分辨率不同的图像，每一层图像代表原图像的不同尺度。这种多尺度表示在图像处理和分析中具有重要意义，可以用于图像金字塔压缩、特征提取和物体检测等任务。

4. 图像降采样

在进行降采样时，如果直接对原始图像进行下采样，可能会丢失图像中的细节和重要信息。高斯模糊使得图像在降采样之前得到平滑处理，从而在降采样过程中保留更多的关键信息，使得金字塔中各层图像能够更好地代表原图像。

举个栗子

该代码构建了三层高斯金字塔

int main() {     string imagePath = "C:\\Users\\Marxist\\Pictures\\coco\\show_jpg.jpg";     string mix_image_path = "C:\\Users\\Marxist\\Pictures\\coco\\Linux.jpg";     Mat image = imread(imagePath);//读取灰度图像     Mat resize_image ;     resize(image,resize_image,Size(500,500));     imshow("source image",resize_image);     Mat g1 ,g2 ,g3;     pyrDown(resize_image,g1,Size(250,250));     pyrDown(g1,g2,Size(125,125));     imshow("g1",g1);     imshow("g2",g2);     waitKey();     return 0; }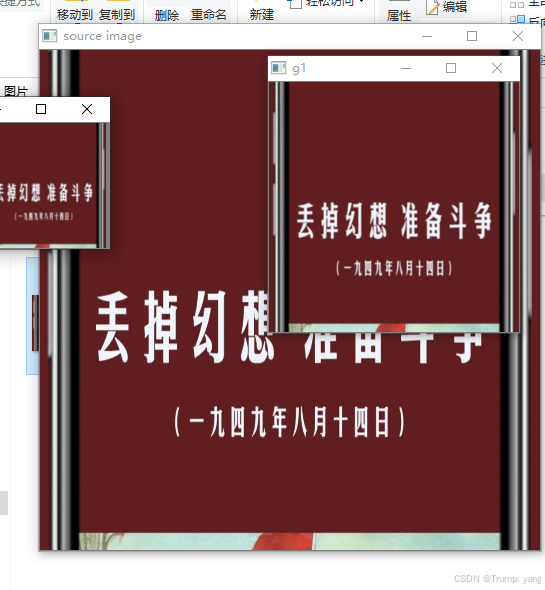 

创建高斯金字塔和拉普拉斯金字塔，并用拉普拉斯金字塔恢复图像

int main() {     string imagePath = "C:\\Users\\Marxist\\Pictures\\coco\\show_jpg.jpg";     string mix_image_path = "C:\\Users\\Marxist\\Pictures\\coco\\Linux.jpg";     Mat image = imread(imagePath);//读取灰度图像     Mat resize_image ;     imshow("source image",image);  //    By default, size of the output image is computed as `Size((src.cols+1)/2, (src.rows+1)/2)`,如果Size不指定，就是默认缩一半 //    pyrDown(resize_image,g1,Size(250,250));      // 构建高斯金字塔     vector<Mat> gaussian_pyramid;     Mat current_image = image;     for (int i = 0; i < 3; ++i) {         Mat down;         pyrDown(current_image, down);         gaussian_pyramid.push_back(down);         current_image = down;     }           // 构建拉普拉斯金字塔     vector<Mat> laplacian_pyramid;     for (int i = 0; i < gaussian_pyramid.size() - 1; ++i) {         Mat up;         pyrUp(gaussian_pyramid[i + 1], up, gaussian_pyramid[i].size());         Mat laplacian = gaussian_pyramid[i] - up;         laplacian_pyramid.push_back(laplacian);     }      // 最顶层高斯金字塔图像也加入拉普拉斯金字塔     laplacian_pyramid.push_back(gaussian_pyramid.back());      // 显示拉普拉斯金字塔     for (int i = 0; i < laplacian_pyramid.size(); ++i) {         imshow("Laplacian Pyramid Level " + to_string(i + 1), laplacian_pyramid[i]);     }      // 从拉普拉斯金字塔恢复原始图像     Mat reconstructed_image = laplacian_pyramid.back(); // 从最顶层开始     for (int i = laplacian_pyramid.size() - 2; i >= 0; --i) {         Mat up;         pyrUp(reconstructed_image, up, laplacian_pyramid[i].size());         reconstructed_image = up + laplacian_pyramid[i];     }      // 显示恢复的图像     imshow("Reconstructed Image", reconstructed_image);      waitKey(0);      return 0; }