数据结构十大习题|part3
七.密码子检索
非常巧妙的设计,请看VCR(bushi):
实验内容:
通用遗传密码表如下: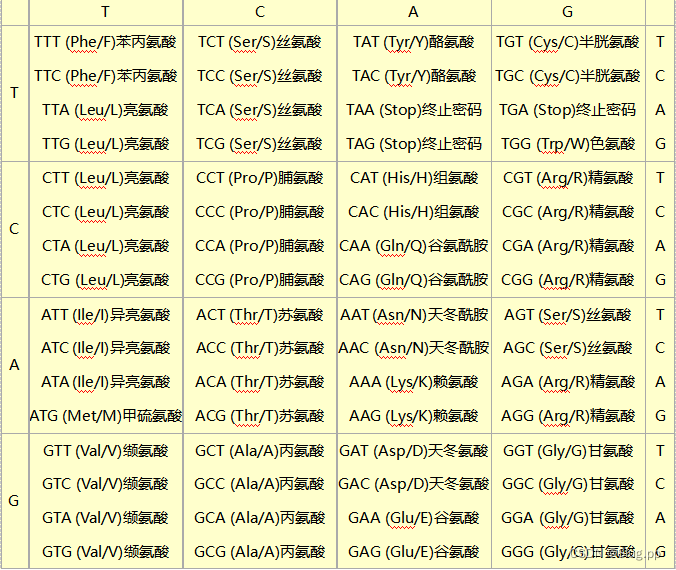
实验要求完成程序编写,以实现密码子检索(查找密码子表),即对给定的密码子,通过查找输出其编码的氨基酸。
例如:给定密码子CTA,其编码的氨基酸是Leu(亮氨酸);又如密码子GAA检索结果是Glu(谷氨酸);再如密码子TAG编码的是Stop(TAG是蛋白质翻译时的3个终止密码之一)。输入与输出文件格式如下:
数据输入文件是若干密码子构成的编码某蛋白质的DNA序列(基因),如:
ATGGTTAAAGTTTATGCCCCGGCTTCCAGTGCCAATATGAGCGTCGGGTTTGATGTGCTCGGGGCGGCGGTGACACCTGTTGATGGTGCATTGCTCGGAGATGTAGTCACGGTTGAGGCGGCAGAGACATTCAGTCTCAACAACCTCGGACGCTTTGCCGATAAGCTGCCGTCAGAACCACGGGAAAATATCGTTTATCAGTGCTGGGAGCGTTTTTGCCAGGAACTGGGTAAGCAAATTCCAGTGGCGATGACCCTGGAAAAGAATATGCCGATCGGTTCGGGCTTAGGCTCCAGTGCCTGTTCGGTGGTCGCGGCGCTGATGGCGATGAATGAACACTGCGGCAAGCCGCTTAATGACACTCGTTTGCTGGCTTTGATGGGCGAGCTGGAAGGCCGTATCTCCGGCAGCATTCATTACGACAACGTGGCACCGTGTTTTCTCGGTGGTATGCAGTTGATGATCGAAGAAAACGACATCATCAGCCAGCAAGTGCCAGGGTTTGATGAGTGGCTGTGGGTGCTGGCGTATCCGGGGATTAAAGTCTCGACGGCAGAAGCCAGGGCTATTTTACCGGCGCAGTATCGCCGCCAGGATTGCATTGCGCACGGGCGACATCTGGCAGGCTTCATTCACGCCTGCTATTCCCGTCAGCCTGAGCTTGCCGCGAAGCTGATGAAAGATGTTATCGCTGAACCCTACCGTGAACGGTTACTGCCAGGCTTCCGGCAGGCGCGGCAGGCGGTCGCGGAAATCGGCGCGGTAGCGAGCGGTATCTCCGGCTCCGGCCCGACCTTGTTCGCTCTGTGTGACAAGCCGGAAACCGCCCAGCGCGTTGCCGACTGGTTGGGTAAGAACTACCTGCAAAATCAGGAAGGTTTTGTTCATATTTGCCGGCTGGATACGGCGGGCGCACGAGTACTGGAAAACTAA
经过逐个密码子的检索,输出其编码的氨基酸序列,最后一个终止密码不翻译。输出文件的格式如下:
MetValLysValTyrAlaProAlaSerSerAlaAsnMetSerValGlyPheAspValLeuGlyAlaAlaValThrProValAspGlyAlaLeuLeuGlyAspValValThrValGluAlaAlaGluThrPheSerLeuAsnAsnLeuGlyArgPheAlaAspLysLeuProSerGluProArgGluAsnIleValTyrGlnCysTrpGluArgPheCysGlnGluLeuGlyLysGlnIleProValAlaMetThrLeuGluLysAsnMetProIleGlySerGlyLeuGlySerSerAlaCysSerValValAlaAlaLeuMetAlaMetAsnGluHisCysGlyLysProLeuAsnAspThrArgLeuLeuAlaLeuMetGlyGluLeuGluGlyArgIleSerGlySerIleHisTyrAspAsnValAlaProCysPheLeuGlyGlyMetGlnLeuMetIleGluGluAsnAspIleIleSerGlnGlnValProGlyPheAspGluTrpLeuTrpValLeuAlaTyrProGlyIleLysValSerThrAlaGluAlaArgAlaIleLeuProAlaGlnTyrArgArgGlnAspCysIleAlaHisGlyArgHisLeuAlaGlyPheIleHisAlaCysTyrSerArgGlnProGluLeuAlaAlaLysLeuMetLysAspValIleAlaGluProTyrArgGluArgLeuLeuProGlyPheArgGlnAlaArgGlnAlaValAlaGluIleGlyAlaValAlaSerGlyIleSerGlySerGlyProThrLeuPheAlaLeuCysAspLysProGluThrAlaGlnArgValAlaAspTrpLeuGlyLysAsnTyrLeuGlnAsnGlnGluGlyPheValHisIleCysArgLeuAspThrAlaGlyAlaArgValLeuGluAsn
相关知识及解题思路:
密码子是指在DNA或RNA中,由三个碱基组成的一个单位,用于编码一个氨基酸。氨基酸是构成蛋白质的基本单元,有20种不同的类型。密码子和氨基酸之间的对应关系称为密码子表,是一种生物学上的常识。
这种查找方法的巧妙之处在于,它利用了密码子的二进制表示和哈希函数的思想,将密码子转换为一个0到63的整数,然后用这个整数作为查找表的下标,直接得到对应的氨基酸。这样可以避免使用复杂的条件判断或循环,提高了查找的效率和简洁性。
转换方式如下: ***
*将密码子中的每个碱基(A, C, G, T)用二进制表示,即T为00,G为01,A为10,C为11。
将密码子中的三个碱基的二进制表示拼接起来,得到一个6位的二进制数,例如CTA为110010。
将这个6位的二进制数分成三个2位的二进制数,分别表示d1, d2, d3,例如110010分成11, 00, 10,分别表示d1, d2, d3。
将这三个0到3的整数组合成一个0到63的整数,即i=4(4d1+d2)+d3,例如0, 0, 0组合成0;0, 0, 1组合成1;0, 0, 2组合成2;…;3, 3, 3组合成63。
用这个0到63的整数作为查找表的下标,直接得到对应的氨基酸,例如0对应Phe,1对应Leu,2对应Leu,…,63对应Pro。
代码框架及实现:
框架:
#include <iostream> #include <stdio.h> #include <string.h> using namespace std; #define seqLen 4096 //*********** 查找表存储结构 ***********// //=====================================// void SearchCodon(char codon[],char AA[]) // 密码子查找(依据密码子codon[],确定氨基酸AA[]) {//*********************************// //==================================// } int main() { char DNA[seqLen]="", Pro[seqLen]=""; // 分别存储DNA和蛋白质序列 char codon[3]; // 存储当前密码子 char AA[3]; // 存储氨基酸 int i, NumOfCodon, p=0; freopen("exp10.in", "r", stdin); freopen("exp10.out", "w", stdout); cin>>DNA; NumOfCodon=strlen(DNA)/3-1; for(i=0; i<NumOfCodon; i++) { codon[0]=DNA[i*3]; codon[1]=DNA[i*3+1]; codon[2]=DNA[i*3+2]; SearchCodon(codon,AA); Pro[p++]=AA[0]; Pro[p++]=AA[1]; Pro[p++]=AA[2]; } Pro[p]='\0'; cout<<Pro<<endl; return 0; } 实现:
#include <iostream> #include <stdio.h> #include <string.h> using namespace std; #define seqLen 4096 //*********** 查找表存储结构 ***********// char hash[64][4]={"Phe", "Leu", "Leu", "Phe", "Cys", "Trp", "###", "Cys", "Tyr", "###", "###", "Tyr", "Ser", "Ser", "Ser", "Ser", "Val", "Val", "Val", "Val", "Gly", "Gly", "Gly", "Gly", "Asp", "Glu", "Glu", "Asp", "Ala", "Ala", "Ala", "Ala", "Ile", "Met", "Ile", "Ile", "Ser", "Arg", "Arg", "Ser", "Asn", "Lys", "Lys", "Asn", "Thr", "Thr", "Thr", "Thr", "Leu", "Leu", "Leu", "Leu", "Arg", "Arg", "Arg", "Arg", "His", "Gln", "Gln", "His", "Pro", "Pro", "Pro", "Pro"}; //=====================================// void SearchCodon(char codon[],char AA[]) // 密码子查找(依据密码子codon[],确定氨基酸AA[]) {//*********************************// int i, d1, d2, d3; d1=((codon[0]>>4) ^ (codon[0] & 0x0F))>>1; d2=((codon[1]>>4) ^ (codon[1] & 0x0F))>>1; d3=((codon[2]>>4) ^ (codon[2] & 0x0F))>>1; i=4*(4*d1+d2)+d3; AA[0]=hash[i][0]; AA[1]=hash[i][1]; AA[2]=hash[i][2]; //==================================// } int main() { char DNA[seqLen]="", Pro[seqLen]=""; // 分别存储DNA和蛋白质序列 char codon[3]; // 存储当前密码子 char AA[3]; // 存储氨基酸 int i, NumOfCodon, p=0; freopen("exp10.in", "r", stdin); freopen("exp10.out", "w", stdout); cin>>DNA; NumOfCodon=strlen(DNA)/3-1; for(i=0; i<NumOfCodon; i++) { codon[0]=DNA[i*3]; codon[1]=DNA[i*3+1]; codon[2]=DNA[i*3+2]; SearchCodon(codon,AA); Pro[p++]=AA[0]; Pro[p++]=AA[1]; Pro[p++]=AA[2]; } Pro[p]='\0'; cout<<Pro<<endl; return 0; } 我没有添加注释,接下来我对这段代码进行说明:
首先DNA密码子是由四种核苷酸(A、T、G、C)组成的。每个碱基可以用两个比特表示,即00、01、10、11。因此,三个碱基共占用6个比特,可以表示64种可能的组合。
接着通过对每个碱基进行位运算,将其两个比特的信息合并成一个比特,从而将三个碱基的信息合并成一个6比特的值。这个值直接对应于64种可能的组合中的一种。
然后是计算查找表的索引,通过将三个碱基的信息合并成的6比特的值进行一些位运算(如右移、异或等),得到一个在0到63之间的整数。这个整数作为查找表的索引,直接对应于生物学遗传密码表中的相应氨基酸。
最后是设计查找表,查找表是一个一维数组,其中每个元素是一个字符串,表示对应的氨基酸。这种设计使得通过计算得到的索引可以直接用于访问查找表中的元素,从而获得相应的氨基酸。
// 以 codon[3] 为例,表示三个碱基的序列 int d1, d2, d3; // 对每个碱基进行位运算,将其两个比特的信息合并成一个比特 d1 = ((codon[0] >> 4) ^ (codon[0] & 0x0F)) >> 1; d2 = ((codon[1] >> 4) ^ (codon[1] & 0x0F)) >> 1; d3 = ((codon[2] >> 4) ^ (codon[2] & 0x0F)) >> 1; // 合并三个碱基的信息得到一个 6 比特的值 int index = 4 * (4 * d1 + d2) + d3; 现在,让我们通过一个具体的例子来说明这个过程:
假设有一个密码子 codon,其三个碱基的信息如下(假设每个碱基用两个比特表示):
codon[0]: 11010011
codon[1]: 10101001
codon[2]: 01101110
对每个碱基进行位运算:
// 对第一个碱基 d1 = ((11010011 >> 4) ^ (11010011 & 0x0F)) >> 1; // 得到 d1 的值 // 对第二个碱基 d2 = ((10101001 >> 4) ^ (10101001 & 0x0F)) >> 1; // 得到 d2 的值 // 对第三个碱基 d3 = ((01101110 >> 4) ^ (01101110 & 0x0F)) >> 1; // 得到 d3 的值 假设计算得到的 d1、d2、d3 分别为 3、2、1。然后,通过这三个值合并得到一个 6 比特的值:
int index = 4 * (4 * 3 + 2) + 1; // 计算索引值 这里的 index 就是查找表中的索引,用于直接访问对应的氨基酸。这个例子中的 index 可能是一个介于 0 到 63 之间的整数,具体值取决于密码子的具体信息。这个整数将直接映射到查找表中的相应位置,从而获取对应的氨基酸。
八.最最最经典的八大排序
这块我就不做详细解释了,各大博主都已经写好了,推一个朋友 的博文:
八大排序(时间复杂度等的对比,基本原理,代码实现)
代码段如下,大家需要自取:
#include <iostream> #include <iomanip> #include <stdio.h> using namespace std; void sort_selection(int L[], int n, int &cn, int &sn) // 简单选择排序 { int i, j, k; int temp; for(i=0; i<n-1; i++) { k=i; for(j=i+1; j<n; j++) { if(L[j]<L[k]) k=j; cn++; } if(k!=i) { temp=L[i]; L[i]=L[k]; L[k]=temp; sn=sn+3; } } } void sort_Shell(int L[], int n, int &cn, int &sn) // 希尔排序 { int i, j, gap=n/2; int temp; while(gap>=1) { for(i=gap; i<n; i++) { cn++; if(L[i]<L[i-gap]) { temp=L[i]; sn++; j=i-gap; do { L[j+gap]=L[j]; sn++; j=j-gap; cn++; }while(j>=0 && temp<L[j]); if (j<0) cn--; L[j+gap]=temp; sn++; } } gap=gap/2; } } int partition(int L[],int p1,int p2,int &cn, int &sn) // 快速排序一趟分割, 返回分割点 { int temp=L[p1]; sn++; while (p1<p2) { while((p1<p2)&&(L[p2]>temp)) { p2--; cn++; } if(p1<p2) cn++; L[p1]=L[p2]; sn++; while((p1<p2)&&(L[p1]<=temp)) { p1++; cn++; } if(p1<p2) cn++; L[p2]=L[p1]; sn++; } L[p2]=temp; sn++; return p2; } void sort_quick(int L[], int n, int &cn, int &sn) // 快速排序 { int stack[256], top=-1; int low, up, mid; stack[++top]=0; stack[++top]=n-1; while(top!=-1) { up=stack[top--]; low=stack[top--]; mid=partition(L,low,up,cn,sn); if(low<mid-1) { stack[++top]=low; stack[++top]=mid-1; } if(mid+1<up) { stack[++top]=mid+1; stack[++top]=up; } } } /* void sort_quick(int L[],int s,int t,int &cn, int &sn) // 快速排序 { int m; if(s<t) { m=partition(L,s,t,cn,sn); sort_quick(L,s,m-1,cn,sn); sort_quick(L,m+1,t,cn,sn); } } */ void heap_sift(int L[],int s,int t,int &cn,int &sn) // 堆排序中的一次筛选 { int i,j; int temp=L[s]; sn++; i=s; j=2*i+1; while(j<=t) { if((j<t)&&(L[j]<L[j+1])) j++; if(j<t) cn++; cn++; if(temp>=L[j]) break; L[i]=L[j]; sn++; i=j; j=2*i+1; } L[i]=temp; sn++; } void sort_heap(int L[],int n,int &cn,int &sn) // 堆排序 { int i; int temp; for (i=n/2-1; i>=0; i--) heap_sift(L,i,n-1,cn,sn); for (i=n-1;i>0;i--) { temp=L[0]; L[0]=L[i]; L[i]=temp; sn=sn+3; heap_sift(L,0,i-1,cn,sn); } } void merge(int *L,int *LL,int s,int m,int t,int &cn,int &sn) // 两个相邻有序子序列的合并 { // 将有序表L[s..m]与有序表L[m+1..t]合并到LL[s..t] int i,j,k; i=s; j=m+1; k=s; while((i<=m)&&(j<=t)) { if(L[i]<=L[j]) LL[k++]=L[i++]; else LL[k++]=L[j++]; cn++; sn++; } while(i<=m) { LL[k++]=L[i++]; sn++; } while(j<=t) { LL[k++]=L[j++]; sn++; } } void mpass(int *R,int *RR,int h,int n,int &cn,int &sn) // 整个记录区间上相邻有序子序列的合并 { int i=0; while(i<=n-2*h) { merge(R,RR,i,i+h-1,i+2*h-1,cn,sn); i=i+2*h; } if(i+h<n) merge(R,RR,i,i+h-1,n-1,cn,sn); else while(i<n) { RR[i]=R[i]; i++; sn++; } } void sort_merge(int *R,int *RR,int n,int &cn,int &sn) // 二路归并排序 { int h=1; while(h<n) { mpass(R,RR,h,n,cn,sn); h=2*h; mpass(RR,R,h,n,cn,sn); h=2*h; } } void output(char *s, int L[], int n, int cn, int sn) // 输出函数 { int i; cout<<"------ "<<s<<" ------\n"; for(i=0; i<n; i++) { cout<<setw(5)<<L[i]; if((i+1) % 16==0) cout<<endl; // 按每行10个输出 } cout<<"comparison: "<<cn<<", shift: "<<sn<<endl; } int main() { int a[256]; // 存储原始记录 int b[256]; // 存储用于排序的记录和结果 int i, n; // n为记录总数 int cmp_num, sft_num; // 分别存储排序中的记录比较和移动次数 freopen("exp09.in", "r", stdin); freopen("exp09.out", "w", stdout); cin>>n; for(i=0; i<n; i++) cin>>a[i]; // 简单选择排序 // for(i=0; i<n; i++) b[i]=a[i]; cmp_num=0; sft_num=0; sort_selection(b,n,cmp_num,sft_num); output("selection sorting",b,n,cmp_num,sft_num); // 希尔排序 // for(i=0; i<n; i++) b[i]=a[i]; cmp_num=0; sft_num=0; sort_Shell(b,n,cmp_num,sft_num); output("Shell sorting",b,n,cmp_num,sft_num); // 快速排序 // for(i=0; i<n; i++) b[i]=a[i]; cmp_num=0; sft_num=0; sort_quick(b,n,cmp_num,sft_num); // sort_quick(b,0,n-1,cmp_num,sft_num); output("quick sorting",b,n,cmp_num,sft_num); // 堆排序 // for(i=0; i<n; i++) b[i]=a[i]; cmp_num=0; sft_num=0; sort_heap(b,n,cmp_num,sft_num); output("heap sorting",b,n,cmp_num,sft_num); // 二路归并排序 // for(i=0; i<n; i++) b[i]=a[i]; cmp_num=0; sft_num=0; sort_merge(b,a,n,cmp_num,sft_num); output("merging sorting",b,n,cmp_num,sft_num); return 0; } 到这里这些习题就告一段落了,本来就更的慢,放寒假心血来潮想起了这个系列没。更完,如果有问题欢迎指出,指导一下小菜鸟,感谢大家的陪伴。
slug.pp ----- 2024/01/23
