1.二叉树
1.1概念与结构
在树形结构中,我们最常⽤的就是⼆叉树,⼀棵⼆叉树是结点的⼀个有限集合,该集合由⼀个根结点 加上两棵别称为左⼦树和右⼦树的⼆叉树组成或者为空。
1. ⼆叉树不存在度⼤于 2 的结点
2. ⼆叉树的⼦树有左右之分,次序不能颠倒,因此⼆叉树是有序树
1.2满二叉树
⼀个⼆叉树,如果每⼀个层的结点数都达到最⼤值,则这个⼆叉树就是满⼆叉树。也就是说,如果⼀ 个⼆叉树的层数为 K ,且结点总数是 (2的k次方-1) ,则它就是满⼆叉树。
1.3二叉树的性质
⼆叉树性质 根据满⼆叉树的特点可知:
1)若规定根结点的层数为 1 ,则⼀棵⾮空⼆叉树的第i层上最多有 (2 的i-1次方 )个结点
2)若规定根结点的层数为 1 ,则深度为 h 的⼆叉树的最⼤结点数是 (2的h次方-1)
3)若规定根结点的层数为 1 ,具有 n 个结点的满⼆叉树的深度 h = log2 (n + 1) ( log 以2为底, n+1 为对数)
1.4完全二叉树
1、叶子结点只可能在最大的两层上出现,对任意结点,若其右分支下的子孙最大层次为L,则其左分支下的子孙的最大层次必为L 或 L+1;
2、出于简便起见,完全二叉树通常采用数组而不是链表存储。
3、满二叉树一定是完全二叉树,完全二叉树不一定是满二叉树。
4、完全二叉树第i层至多有2的(i-1)次方个节点,共i层的完全二叉树最多有2的i次方-1个节点。
5、只允许最后一层有空缺结点且空缺在右边,即叶子结点只能在层次最大的两层上出现;
6、对任一结点,如果其右子树的深度为j,则其左子树的深度必为j或j+1。 即度为1的点只有1个或0个。
2.二叉树的存储结构
2.1顺序结构
顺序结构存储就是使⽤数组来存储,⼀般使⽤数组只适合表⽰完全⼆叉树,因为不是完全⼆叉树会有 空间的浪费,完全⼆叉树更适合使⽤顺序结构存储。
2.2链式结构
⼆叉树的链式存储结构是指,⽤链表来表⽰⼀棵⼆叉树,即⽤链来指⽰元素的逻辑关系。 通常的⽅法 是链表中每个结点由三个域组成,数据域和左右指针域,左右指针分别⽤来给出该结点左孩⼦和右孩 ⼦所在的链结点的存储地址 。
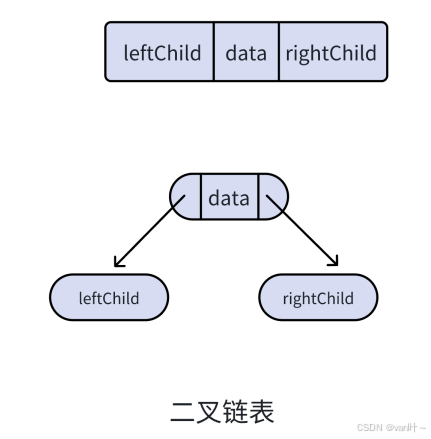
2.3实现链式结构⼆叉树
typedef int BTDataType; // ⼆叉链 typedef struct BinaryTreeNode { struct BinTreeNode* left; // 指向当前结点左孩⼦ struct BinTreeNode* right; // 指向当前结点右孩⼦ BTDataType val; // 当前结点值域 }BTNode; BTNode* BuyBTNode(int val) { BTNode* newnode = (BTNode*)malloc(sizeof(BTNode)); if (newnode == NULL) { perror("malloc fail"); return NULL; } newnode->val = val; newnode->left = NULL; newnode->right = NULL; return newnode; } //初始化3.功能实现
3.1 销毁二叉树
void BinaryTreeDestory(BTnode** root)//要传二级指针,因为要改变根节点为NULL;而根节点是指针,改变指针需要传二级指针 { if(*root==NULL) return; BinaryTreeDestory(&((*root)->left)); BinaryTreeDestory(&((*root)->right)); free(*root); *root=NULL; }3.2 层序遍历(!!!!!)
单纯递归是无法解决层序遍历问题的,实现层序遍历需要额外借助数据结构:队列(!!!!!)
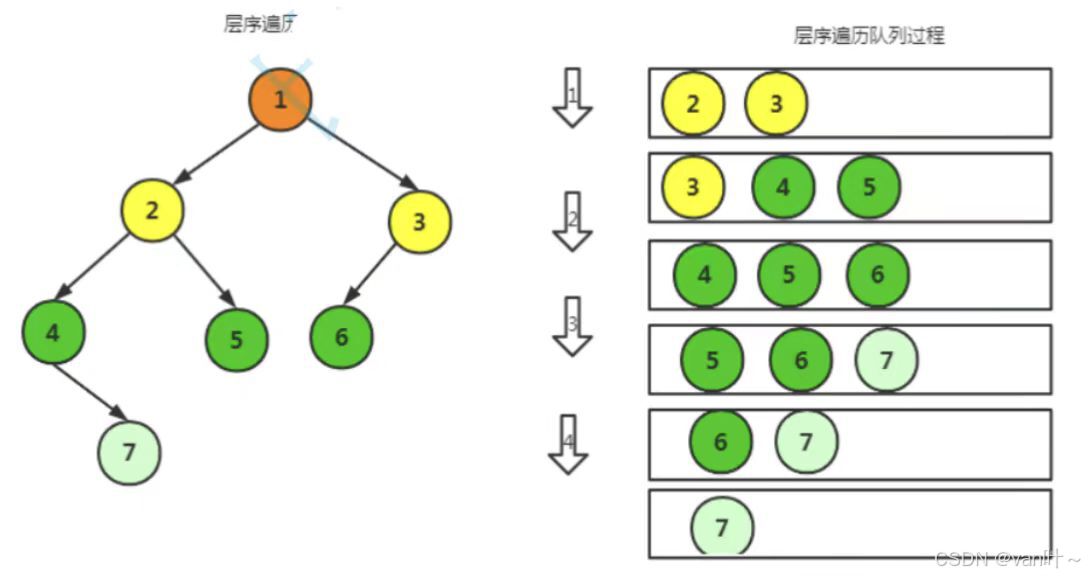
// 层序遍历 void LevelOrder(BTNode* root) { Queue q; QueueInit(&q); QueuePush(&q, root); while (!QueueEmpty(&q)) { BTNode* top = QueueFront(&q); printf("%c ", top->data); QueuePop(&q); if (top->_left) { QueuePush(&q, top->_left); } if (top->_right) { QueuePush(&q, top->_right); } } QueueDesTroy(&q); }3.3判断是否为完全⼆叉树
// 判断⼆叉树是否是完全⼆叉树 bool BinaryTreeComplete(BTNode* root) { Queue q; QueueInit(&q); QueuePush(&q, root); while (!QueueEmpty(&q)) { BTNode* top = QueueFront(&q); QueuePop(&q); if (top == NULL) { break; } QueuePush(&q, top->_left); QueuePush(&q, top->_right); } while (!QueueEmpty(&q)) //如果为完全二叉树,只允许最后一层有空缺节点,且在右边,所以最后队列的元素一定只有NULL(可能有好几个NULL) { BTNode* top = QueueFront(&q); QueuePop(&q); if (top != NULL) //不是NULL,一定不是完全二叉树 { QueueDesTroy(&q); return false; } } QueueDesTroy(&q); return true; }