图中的最短环

2608. 图中的最短环

现有一个含 n 个顶点的 双向 图，每个顶点按从 0 到 n - 1 标记。图中的边由二维整数数组 edges 表示，其中 edges[i] = [ui, vi] 表示顶点 ui 和 vi 之间存在一条边。每对顶点最多通过一条边连接，并且不存在与自身相连的顶点。

返回图中 最短 环的长度。如果不存在环，则返回 -1 。

环 是指以同一节点开始和结束，并且路径中的每条边仅使用一次。

示例 1：

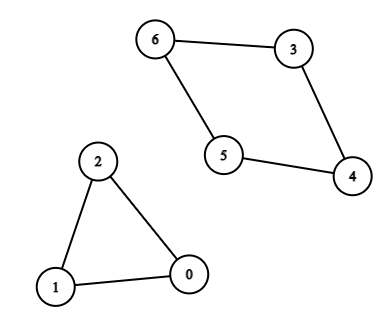
**输入：**n = 7, edges = [[0,1],[1,2],[2,0],[3,4],[4,5],[5,6],[6,3]] **输出：**3 **解释：**长度最小的循环是：0 -> 1 -> 2 -> 0 

示例 2：

**输入：**n = 4, edges = [[0,1],[0,2]] **输出：**-1 **解释：**图中不存在循环 

提示：

• 2 <= n <= 1000
• 1 <= edges.length <= 1000
• edges[i].length == 2
• 0 <= ui, vi < n
• ui != vi
• 不存在重复的边

还是删除边比较容易写

class Solution { public:     int findShortestCycle(int n, vector<vector<int>>& edges) {         for (int i = 0; i < 1000; i++) fa[i] = i;         vector<pair<int, int>> sto; // 存储环的起始和结束节点         for (auto u : edges) {             int x = find(u[0]), y = find(u[1]);             if (x != y) {                 fa[x] = y;             }             else {                 sto.push_back({ u[0],u[1] });             }             e[u[0]].push_back(u[1]);             e[u[1]].push_back(u[0]);         }         if (sto.size() == 0) return -1;         int ans = 0xffffff;         for (auto [u,v] : sto) {             queue<pair<int, int>> q;             vector<bool> vis(n + 1, 0);             q.push({ u,1 });             while (q.size()) {                 auto [node, step] = q.front(); q.pop();                 if (node == v) {                     ans = min(ans, step); break;                 }                 if (vis[node]) continue;                 vis[node] = 1;                 for (auto to : e[node]) {                     if (node == u && to == v) continue; // 跳开一条断边                     q.push({ to,step + 1 });                 }             }         }         return ans;     }      int find(int x) {         if (x == fa[x]) return x;         return fa[x] = find(fa[x]);     }      int fa[1001];     vector<int> e[1001];      }; 

我们再看一个题目，如果权重

#define _CRT_SECURE_NO_WARNINGS #include<bits/stdc++.h> using namespace std;  const int N = 105; int e[N][N]; int n,m; const int M = (int)5e3+5; int edge[M],ne[M],h[N],idx = 0; int w[M]; int fa[N];  void add(int a,int b,int wei){ 	edge[++idx] = b, ne[idx] = h[a], h[a] = idx; 	w[idx] = wei; }  int find(int x){ 	if(x==fa[x]) return x; 	return fa[x] = find(fa[x]); }   int main(){ 	cin >> n >> m; 	// 开始处理fa 	for(int i=0;i<=n;i++) fa[i] = i;  	vector<pair<int,int>> sto; 	for(int i=1;i<=m;i++){ 		int u,v,d; 		cin >> u >> v >> d; 		if(e[u][v]==0){ 			e[u][v] = d; 			e[v][u] = d; 		}else{ 			if(e[u][v]>d){ 				e[u][v] = d; 				e[v][u] = d; 			} 		} 	}	 	for(int i=1;i<=n;i++){ 		for(int j=1;j<=i;j++){ 			if(e[i][j]){ 				int x = find(i), y = find(j); 				if(x!=y) fa[x] = y; 				else { 					sto.push_back({i,j}); 				} 				add(i,j,e[i][j]); 				add(j,i,e[i][j]); 			} 		} 	} //	if(sto.size()==0) { //		cout << "No solution."; return 0; //	} 	int ans = 0x7fffffff; 	for(auto x:sto){ 		vector<bool> vis(n+1); 		int u = x.first, v = x.second; 		priority_queue<pair<int,int>> q; 		q.push({0,u}); 		while(q.size()){ 			int d = -q.top().first, node = q.top().second; q.pop(); 			if(vis[node]) continue; 			vis[node] = 1; 			if(node==v){ 				ans = min(ans,d+e[v][u]); break; 			} 			for(int i=h[node];i;i=ne[i]){ 				int to = edge[i], ww = w[i]; 				if(node==u&&to==v) continue; 				q.push({-(d+ww),to}); 			} 		} 	} 	if(ans!=0x7fffffff) 	cout << ans; 	else cout << "No solution.";  	return 0; }