STL List and Vector 总结

avatar
作者
筋斗云
阅读量:0

Vector

深浅拷贝

深浅拷贝是什么

  • 浅拷贝
    • 浅拷贝是复制对象的值，包括指针变量的地址，而不是指针所指向的实际数据
    • 原始对象与复制对象共享相同的内存地址，如果修改其中一个对象的数据，则另一个对象的数据也会被修改，因为两者指向同一片内存地址空间
    • 如果数据改动或者存储地址变化时，会导致同一块内存被多次释放，从而导致内存泄漏或者程序崩溃
  • 深拷贝
    • 赋值对象的值以及指针变量所指向的实际数据
    • 原始对象和复制对象拥有各自独立的内存空间，互不影响

浅拷贝实验 

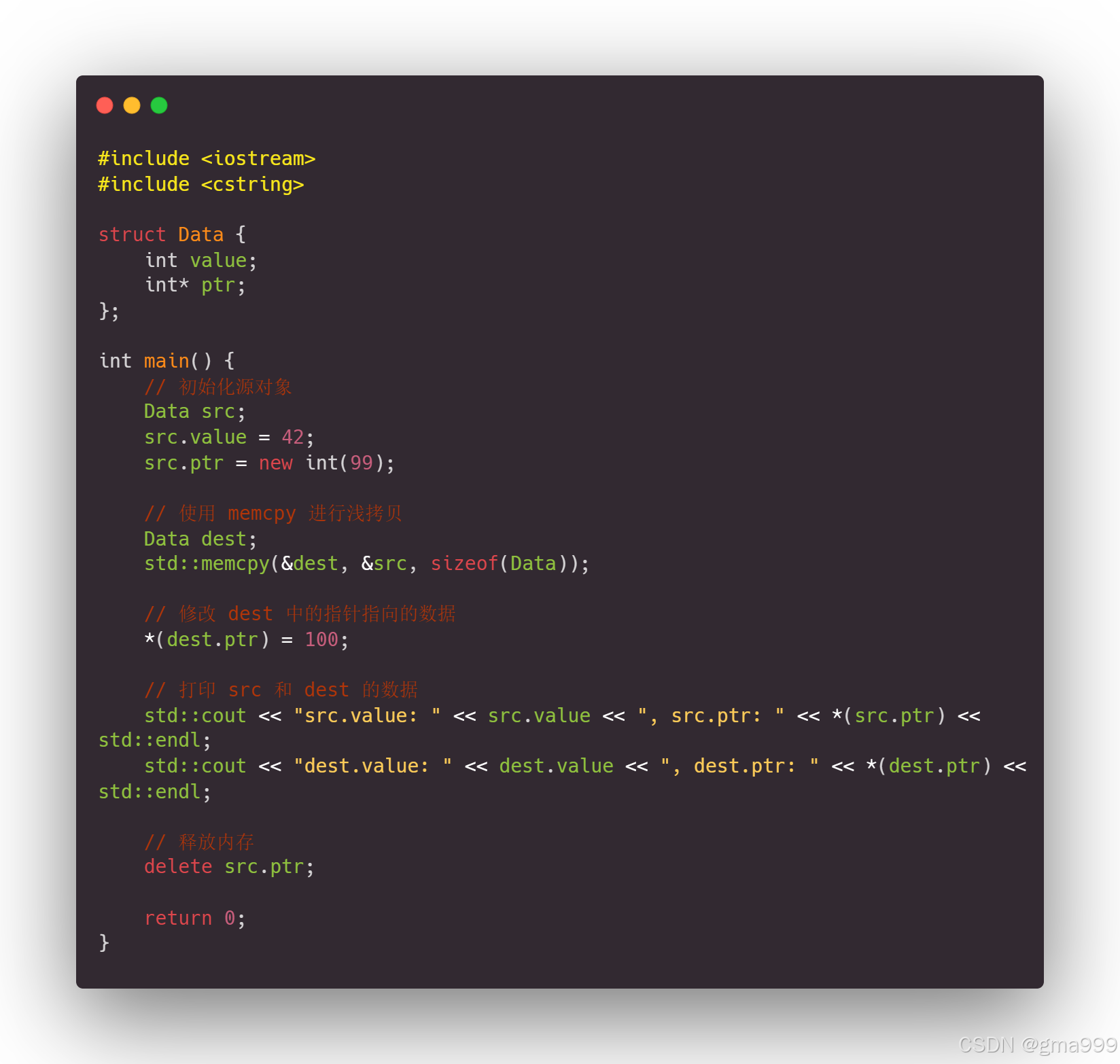
实现原理

vector是一个动态数组容器，提供动态大小的数组功能，允许快速的随机访问以及高效的添加、删除和插入操作。

  • 数据结构
    • 指向数据的指针：指向存储元素的动态数组
    • 当前大小：当前存储有效元素的数量
    • 容量：当前分配的内存空间，可以容纳的最大元素数量
  • 动态内存分配 
    • 当需要更多空间时，vector会自动分配内存块，并将现有元素复制到新内存中
    • 增加容量
      • vs下是1.5倍增长
      • g++下是2.0倍增长
    • reserve只负责开辟空间，resize则是开辟空间的同时对其初始化

自我实现

核心功能实现：扩容和尾插

#include <iostream>  template <typename T> class SimpleVector { private:     T* data;       // 指向数据的指针     size_t size;   // 当前元素个数     size_t capacity; // 容量      // 扩容函数     void resizeIfNeeded() {         if (size >= capacity) {             size_t newCapacity = capacity == 0 ? 1 : 2 * capacity;             T* newData = new T[newCapacity];             for (size_t i = 0; i < size; ++i) {                 newData[i] = std::move(data[i]);             }             delete[] data;             data = newData;             capacity = newCapacity;         }     }  public:     // 构造函数     SimpleVector() : data(nullptr), size(0), capacity(0) {}      // 析构函数     ~SimpleVector() {         delete[] data;     }      // 尾部添加元素     void push_back(const T& value) {         resizeIfNeeded();         data[size++] = value;     }      // 获取大小     size_t getSize() const {         return size;     }      // 获取容量     size_t getCapacity() const {         return capacity;     }      // 访问元素     T& operator[](size_t index) {         return data[index];     }      // 访问元素（const）     const T& operator[](size_t index) const {         return data[index];     } };  int main() {     SimpleVector<int> vec;     vec.push_back(1);     vec.push_back(2);     vec.push_back(3);      for (size_t i = 0; i < vec.getSize(); ++i) {         std::cout << vec[i] << " ";     }     std::cout << std::endl;      std::cout << "Size: " << vec.getSize() << std::endl;     std::cout << "Capacity: " << vec.getCapacity() << std::endl;      SimpleVector<char> vChar;     vChar.push_back('m');      std::cout<<vChar[0]<<std::endl;      return 0; }

List

自我实现

List插入（头插、尾插、指定位置插入）

template <typename T> class List { private:     Node<T>* head;     Node<T>* tail;     size_t size;  public:     // 构造函数     List() : head(nullptr), tail(nullptr), size(0) {}      // 析构函数     ~List() {         clear();     }      // 清空链表     void clear() {         while (head != nullptr) {             Node<T>* temp = head;             head = head->next;             delete temp;         }         tail = nullptr;         size = 0;     }      // 获取大小     size_t getSize() const {         return size;     }      // 插入元素     void insert(size_t position, const T& value) {         if (position > size) {             throw std::out_of_range("Position out of range");         }          Node<T>* newNode = new Node<T>(value);         if (position == 0) {             // 插入到头部             newNode->next = head;             if (head != nullptr) {                 head->prev = newNode;             }             head = newNode;             if (tail == nullptr) {                 tail = newNode;             }         } else if (position == size) {             // 插入到尾部             newNode->prev = tail;             if (tail != nullptr) {                 tail->next = newNode;             }             tail = newNode;             if (head == nullptr) {                 head = newNode;             }         } else {             // 插入到中间             Node<T>* current = head;             for (size_t i = 0; i < position; ++i) {                 current = current->next;             }             newNode->next = current;             newNode->prev = current->prev;             current->prev->next = newNode;             current->prev = newNode;         }         ++size;     }      // 打印链表     void print() const {         Node<T>* current = head;         while (current != nullptr) {             std::cout << current->data << " ";             current = current->next;         }         std::cout << std::endl;     } };

细节问题分析

List和vector的区别

  • vector是一个动态数组，支持动态数组，支持快速的随机访问。时间复杂度为O（1），如果是在中间插入或者删除元素时候，需要移动大量元素，此时的时间复杂度为O（n）。Vector适用于频繁随机访问的场景
  • List则是一个双向链表，插入和删除非常高效，时间复杂度为O（1），但是随机访问元素的时候需要遍历，事件复杂度O（N）。List适用于频繁中间插入或删除元素的场景

迭代器失效

List迭代器不会失效的原因（不绝对）

  • List的底层为双向链表结构，插入和删除元素只需要调整相邻节点指针，不会影响其他节点和节点的指针，所以其他迭代器保持有效
  • 只有指向被删除节点的迭代器才会失效，而指向其他节点的迭代器不会受到影响

Vector迭代器失效

  • 失效场景
    • 扩容时迭代器失效，因为底层数组的内存地址发生了变化，指向旧地址的迭代器不再有效
    • 中间插入或者删除元素时，指定位置插入或者删除元素都可能会导致迭代器失效，因为这些元素的位置发生了变化 

 

数组或链表实现队列结构

数组实现队列：通过环形缓冲区避免数据移动，提高效率。

#include <iostream> #include <stdexcept>  template <typename T> class ArrayQueue { private:     T* data;     size_t capacity;     int front;     int rear;     size_t count;  public:     // 构造函数     ArrayQueue(size_t capacity) : capacity(capacity), front(0), rear(-1), count(0) {         data = new T[capacity];     }      // 析构函数     ~ArrayQueue() {         delete[] data;     }      // 入队操作     void enqueue(const T& value) {         if (count == capacity) {             throw std::overflow_error("Queue overflow");         }         rear = (rear + 1) % capacity;         data[rear] = value;         ++count;     }      // 出队操作     void dequeue() {         if (count == 0) {             throw std::underflow_error("Queue underflow");         }         front = (front + 1) % capacity;         --count;     }      // 获取队列前端元素     T& peek() {         if (count == 0) {             throw std::underflow_error("Queue is empty");         }         return data[front];     }      // 判断队列是否为空     bool isEmpty() const {         return count == 0;     }      // 获取队列的大小     size_t size() const {         return count;     } };  // 测试代码 int main() {     ArrayQueue<int> queue(10);     queue.enqueue(1);     queue.enqueue(2);     queue.enqueue(3);      std::cout << "Front element: " << queue.peek() << std::endl;      queue.dequeue();     std::cout << "Front element after dequeue: " << queue.peek() << std::endl;      std::cout << "Queue size: " << queue.size() << std::endl;      return 0; }

使用链表实现队列：通过链表的尾部插入以及头删操作实现入队和出队 

#include <iostream> #include <stdexcept>  template <typename T> struct Node {     T data;     Node* next;      Node(const T& value) : data(value), next(nullptr) {} };  template <typename T> class LinkedListQueue { private:     Node<T>* front;     Node<T>* rear;     size_t count;  public:     // 构造函数     LinkedListQueue() : front(nullptr), rear(nullptr), count(0) {}      // 析构函数     ~LinkedListQueue() {         while (front != nullptr) {             dequeue();         }     }      // 入队操作     void enqueue(const T& value) {         Node<T>* newNode = new Node<T>(value);         if (rear) {             rear->next = newNode;         } else {             front = newNode;         }         rear = newNode;         ++count;     }      // 出队操作     void dequeue() {         if (front == nullptr) {             throw std::underflow_error("Queue underflow");         }         Node<T>* temp = front;         front = front->next;         if (front == nullptr) {             rear = nullptr;         }         delete temp;         --count;     }      // 获取队列前端元素     T& peek() {         if (front == nullptr) {             throw std::underflow_error("Queue is empty");         }         return front->data;     }      // 判断队列是否为空     bool isEmpty() const {         return front == nullptr;     }      // 获取队列的大小     size_t size() const {         return count;     } };  // 测试代码 int main() {     LinkedListQueue<int> queue;     queue.enqueue(1);     queue.enqueue(2);     queue.enqueue(3);      std::cout << "Front element: " << queue.peek() << std::endl;      queue.dequeue();     std::cout << "Front element after dequeue: " << queue.peek() << std::endl;      std::cout << "Queue size: " << queue.size() << std::endl;      return 0; }

数组或链表实现栈结构

链表实现栈：通过链表节点的插入和删除操作来实现入栈和出栈操作

#include <iostream> #include <stdexcept>  template <typename T> struct Node {     T data;     Node* next;      Node(const T& value) : data(value), next(nullptr) {} };  template <typename T> class LinkedListStack { private:     Node<T>* top;     size_t count;  public:     // 构造函数     LinkedListStack() : top(nullptr), count(0) {}      // 析构函数     ~LinkedListStack() {         while (top != nullptr) {             pop();         }     }      // 入栈操作     void push(const T& value) {         Node<T>* newNode = new Node<T>(value);         newNode->next = top;         top = newNode;         ++count;     }      // 出栈操作     void pop() {         if (top == nullptr) {             throw std::underflow_error("Stack underflow");         }         Node<T>* temp = top;         top = top->next;         delete temp;         --count;     }      // 获取栈顶元素     T& peek() {         if (top == nullptr) {             throw std::underflow_error("Stack is empty");         }         return top->data;     }      // 判断栈是否为空     bool isEmpty() const {         return top == nullptr;     }      // 获取栈的大小     size_t size() const {         return count;     } };  // 测试代码 int main() {     LinkedListStack<int> stack;     stack.push(1);     stack.push(2);     stack.push(3);      std::cout << "Top element: " << stack.peek() << std::endl;      stack.pop();     std::cout << "Top element after pop: " << stack.peek() << std::endl;      std::cout << "Stack size: " << stack.size() << std::endl;      return 0; }

数组实现栈：栈顶指针指向当前元素位置，入栈和出栈都在栈顶进行即可 

#include <iostream> #include <stdexcept>  template <typename T> class ArrayStack { private:     T* data;     size_t capacity;     int top;  public:     // 构造函数     ArrayStack(size_t capacity) : capacity(capacity), top(-1) {         data = new T[capacity];     }      // 析构函数     ~ArrayStack() {         delete[] data;     }      // 入栈操作     void push(const T& value) {         if (top == capacity - 1) {             throw std::overflow_error("Stack overflow");         }         data[++top] = value;     }      // 出栈操作     void pop() {         if (top == -1) {             throw std::underflow_error("Stack underflow");         }         --top;     }      // 获取栈顶元素     T& peek() {         if (top == -1) {             throw std::underflow_error("Stack is empty");         }         return data[top];     }      // 判断栈是否为空     bool isEmpty() const {         return top == -1;     }      // 获取栈的大小     size_t size() const {         return top + 1;     } };  // 测试代码 int main() {     ArrayStack<int> stack(10);     stack.push(1);     stack.push(2);     stack.push(3);      std::cout << "Top element: " << stack.peek() << std::endl;      stack.pop();     std::cout << "Top element after pop: " << stack.peek() << std::endl;      std::cout << "Stack size: " << stack.size() << std::endl;      return 0; }

Vector扩容机制及其时间复杂度

push_back 时间复杂度分析

  • 无需扩容时：此时只需要将新元素放入到现有元素的后面，所以时间复杂度为O（1）
  • 需要扩容时：
    • 分配新的内存块；现有元素从旧内存块复制到新内存块中；释放旧内存块；添加新元素
    • 时间复杂度：O(n)
  • 摊销分析
    • 假设初始容量为 1，每次扩容时容量加倍。
    • 第一次扩容时，需要复制 1 个元素，操作耗时 O(1)O(1)O(1)。
    • 第二次扩容时，需要复制 2 个元素，操作耗时 O(2)O(2)O(2)。
    • 第三次扩容时，需要复制 4 个元素，操作耗时 O(4)O(4)O(4)。
    • 依此类推，第 kkk 次扩容时，需要复制 2k−12^{k-1}2k−1 个元素，操作耗时 O(2k−1)O(2^{k-1})O(2k−1)。

    • 假设总共有 nnn 个元素，vector 扩容的次数为 log⁡n\log nlogn 次，总的扩容复制操作耗时为： 1+2+4+⋯+2log⁡n−1=2log⁡n−1=n−11 + 2 + 4 + \cdots + 2^{\log n - 1} = 2^{\log n} - 1 = n - 11+2+4+⋯+2logn−1=2logn−1=n−1

      将这些耗时均摊到每次 push_back 操作上，得到每次操作的平均时间复杂度为 O(1)

Vector插入操作比List慢的原因

  • Vector的插入操作可能存在需要移动大量元素的情况，时间复杂度是O(n)
  • List的插入操作则只需要调整相邻节点的指针，时间复杂度O(1)
相关阅读
  1. 如何查看和设置我的Android N设备的权限？
  2. 如何在安卓手机上自定义应用图标？
  3. 如何在安卓微信中同时听语音和查看图片？
  4. 华为哪些设备将支持升级至安卓7.0？
  5. 微信安卓软件中Q10功能有哪些独特之处？
  6. 安卓用户如何挑选最佳视频播放器应用？
  7. 安卓系统中用户文件目录的确切位置是什么？
  8. 小米4用户如何安全升级到安卓8.0系统？
  9. 如何成功将魅蓝5升级至安卓原生7.0版本？
  10. 16GB存储的安卓手机是否能满足日常需求？

广告一刻

为您即时展示最新活动产品广告消息，让您随时掌握产品活动新动态！