阅读量:0
学习目标：
进一步了解并掌握动态规划
学习内容：
4. LeetCode62. 不同路径
https://leetcode.cn/problems/unique-paths/
5. LeetCode63. 不同路径 IIhttps://leetcode.cn/problems/unique-paths-ii/
6. LeetCode343. 整数拆分https://leetcode.cn/problems/integer-break/
7. LeetCode96. 不同的二叉搜索树https://leetcode.cn/problems/unique-binary-search-trees/
学习产出：
独立解决以上题目
4. LeetCode62. 不同路径
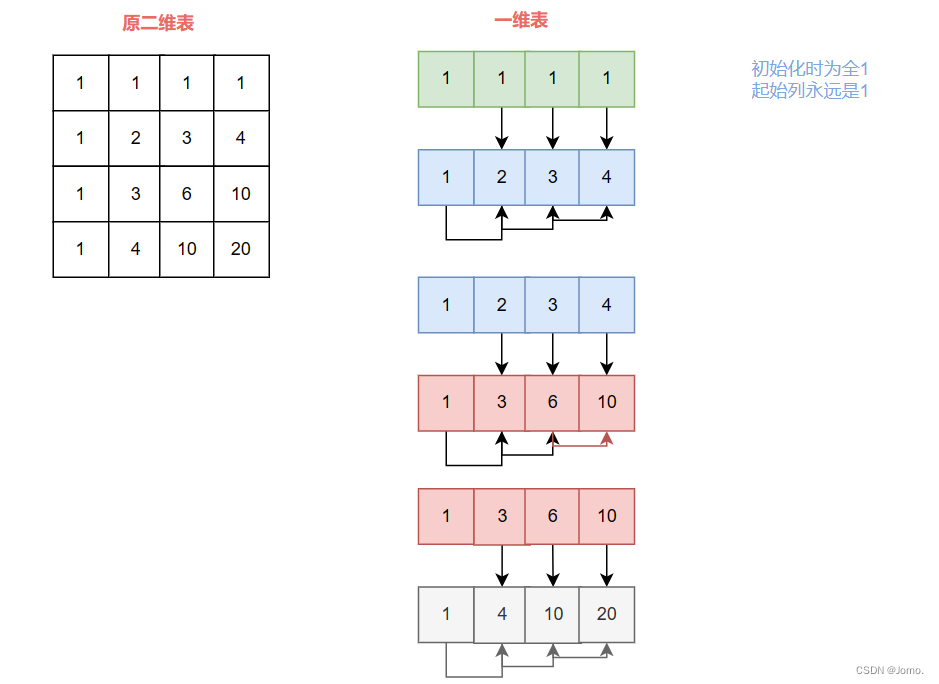
1.动态规划二维表 class Solution { public: int uniquePaths(int m, int n) { //特殊情况 if(m<0||n<0){ return -1; } if(m==0||n==0){ return 1; } //dp[i][j]：机器人到达[i][j]有几种方法 vector<vector<int>>dp(m,vector<int>(n)); //初始化dp(注意边界情况：第0行和第0列) for(int i=0;i<m;i++){ dp[i][0]=1; } for(int j=0;j<n;j++){ dp[0][j]=1; } //由于机器人只能向下或向右移动一格 //因此每一个格子只能从其上或左抵达 //转移方程：dp[i][j]=dp[i-1][j]+dp[i][j-1] //完善dp for(int i=1;i<m;i++){ for(int j=1;j<n;j++){ dp[i][j]=dp[i-1][j]+dp[i][j-1]; } } return dp[m-1][n-1]; } } 时间复杂度：O(m*n) 空间复杂度：O(m*n) 2.动态规划一维表(滚动数组)：我们只需要用到前一行和当前行前一列的变量，所以我们可以利用一张一维表不断更新迭代即可。前面有图片讲解。 class Solution { public: int uniquePaths(int m, int n) { if(m<0||n<0){ return -1; } if(m==0||n==0){ return 1; } //初始化dp vector<int>dp(n,1); for(int i=1;i<m;i++){ for(int j=1;j<n;j++){ dp[j]=dp[j-1]+dp[j]; } } return dp[n-1]; } }; 时间复杂度：O(m*n) 空间复杂度：O(n) 3.数论：排列组合(在总步数m-n-2中选m-1步来向下，其余往右走) 方法数=C(m-n-2)(m-1) class Solution { public: int uniquePaths(int m, int n) { //特殊情况 if(m<0||n<0){ return -1; } if(m==0||n==0){ return 1; } //分子可能会溢出，所以用long long类型 long long numerator=1; //分母是(m-1)的阶乘，但先初始化为m-1，阶乘太大容易溢出，所以在计算过程中看能否约掉 int denominator=m-1; int count=m-1; int t=m+n-2; while(count--){ numerator*=(t--); //判断是否能约,分母不能等于0 while(denominator!=0&&numerator%denominator==0){ numerator/=denominator; denominator--;//因为是阶乘，所以m-1的下一个除数是m-2 } } return numerator; } }; 时间复杂度：O(m) 空间复杂度：O(1) 4.深度优先搜索会超时，二叉树深度为（m+n-1）（深度从1开始），时间复杂度即结点个数为2^(m+n-1)-1，已经是指数级别了。 分析：每个二叉树结点有两个选择：向下或向右。先一直往同一个方向走，到达尽头后，再往另一个方向一直走到尽头，那么深度就是m+n-1了。5. LeetCode63. 不同路径 II
1.动态规划二维表 class Solution { public: int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) { //dp[i][j]：到达[i][j]的方法数 int m=obstacleGrid.size(); int n=obstacleGrid[0].size(); vector<vector<int>>dp(m,vector<int>(n)); //初始化dp，如果第0行和第0列有障碍物，那么其右边或下边的格子无法抵达 for(int i=0;i<m;i++){ if(obstacleGrid[i][0]==1)break; dp[i][0]=1; } for(int j=0;j<n;j++){ if(obstacleGrid[0][j]==1)break; dp[0][j]=1; } //完善dp for(int i=1;i<m;i++){ for(int j=1;j<n;j++){ if(obstacleGrid[i][j]==1){//当前位置是障碍物，走不了，保留0 continue; } //即使左边和上边是障碍物也不影响，因为方法数是0 dp[i][j]=dp[i-1][j]+dp[i][j-1]; } } return dp[m-1][n-1]; } }; 2.滚动数组：优化空间效率 class Solution { public: int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) { int m=obstacleGrid.size(); int n=obstacleGrid[0].size(); if(m==1){ for(int j=0;j<n;j++){ if(obstacleGrid[0][j]==1)return 0; } }else if(n==1){ for(int i=0;i<m;i++){ if(obstacleGrid[i][0]==1)return 0; } } vector<int>dp(n);//滚动数组 //初始化dp for(int j=0;j<n;j++){ if(obstacleGrid[0][j]==1)break; dp[j]=1; } for(int i=1;i<m;i++){ for(int j=0;j<n;j++){//第一列也可能有障碍物 if(obstacleGrid[i][j]==1){ dp[j]=0;//障碍物，需要置为0 continue; } if(j>0)dp[j]=dp[j-1]+dp[j]; } } return dp[n-1]; } };6. LeetCode343. 整数拆分
1.动态规划 class Solution { public: int integerBreak(int n) { //特殊情况 if(n<2){ return 0; } //dp[i]：拆分数字i的最大乘积 vector<int>dp(n+1); //初始化dp dp[2]=1; for(int i=3;i<=n;i++){ for(int j=1;j<=i/2;j++){//3拆分成1和2，所以从1开始 //把i拆分成i-j和j两个数 //或者拆分成j和其他数(数量>1)，只需要直到被拆分数的最大乘积即可 dp[i]=max(dp[i],max((i-j)*j,j*dp[i-j])); } } return dp[n]; } }; 时间复杂度：O(n^2) 空间复杂度：O(n) 2.数论 class Solution { public: int integerBreak(int n) { //特殊情况 if(n==2)return 1; if(n==3)return 2; if(n==4)return 4;//4=(2+2)=>2*2>3*1 int res=1; while(n>4){ res*=3; n-=3; } res*=n; return res; } }; 时间复杂度：O(n) 空间复杂度：O(1)7. LeetCode96. 不同的二叉搜索树
本题我们只用管有i个节点时的结构数，不用管值。因为值都是不同的，所以可以把结构安排好后再把值填入即可。 class Solution { public: int numTrees(int n) { //dp[i]：节点个数为i的二叉搜索树结构数 vector<int>dp(n+1); //初始化dp dp[0]=1; dp[1]=1; for(int i=2;i<=n;i++){//整棵树节点个数 for(int j=0;j<=i-1;j++){//左子树节点个数 dp[i]+=dp[j]*dp[i-j-1]; } } return dp[n]; } };