(又是万恶的 DP ! ! ! )
OK啊,经过一个月的拖更,我又回来了!
请见这长~长~的目录:
目录
跳过目录
前言
背包(Knapsack)问题是经典的动态规划问题,也很有实际价值。
而最经典的背包问题有三种:01背包,多重背包,完全背包。
01背包:
顾名思义,01背包,即每种物品只能取0件或1件。
例题:洛谷P2871

易证,考虑第i+1种物品时,可选择0件或1件。且答案只会利用前i种的利益最大值而与第i+2种选不选无关。(最优子结构+无后效性)
状态设计:
令f[i][j]为考虑前i个物品,容量为j的背包所能装的最大总价值。
转移方程:
取:f[i-1][j-w[i]]+v[i]
不取:f[i-1][j]
取max:f[i][j]=max(f[i-1][j],f[i-1][j-w[i]]+v[i])
代码:
#include <bits/stdc++.h> using namespace std; int f[3403][12881],w[114514],v[114514]; int main(){ int n, m; scanf("%d%d", &n, &m); for(int i = 1; i <= n; i++){ cin >> w[i] >> v[i]; } for(int i = 1; i <= n; i++) for(int j = 0;j <= m; j++) f[i][j]=max(f[i-1][j],f[i-1][j-w[i]]+v[i]); printf("%d\n", f[n][m]); return 0; }优化:
还能滚动数组优化空间为线性。
转移方程:f[i]=max(f[i],f[i-w]+v)
注意倒着更新即可。
优化代码:
#include <bits/stdc++.h> using namespace std; int f[114514]; int main(){ int n, m; scanf("%d%d", &n, &m); while(n--){ int w, v; scanf("%d%d", &w, &v); for(int i=m; i>=w; i--)f[i]=max(f[i], f[i - w] + v); } printf("%d\n", f[m]); return 0; }完全背包:
例题:洛谷P1616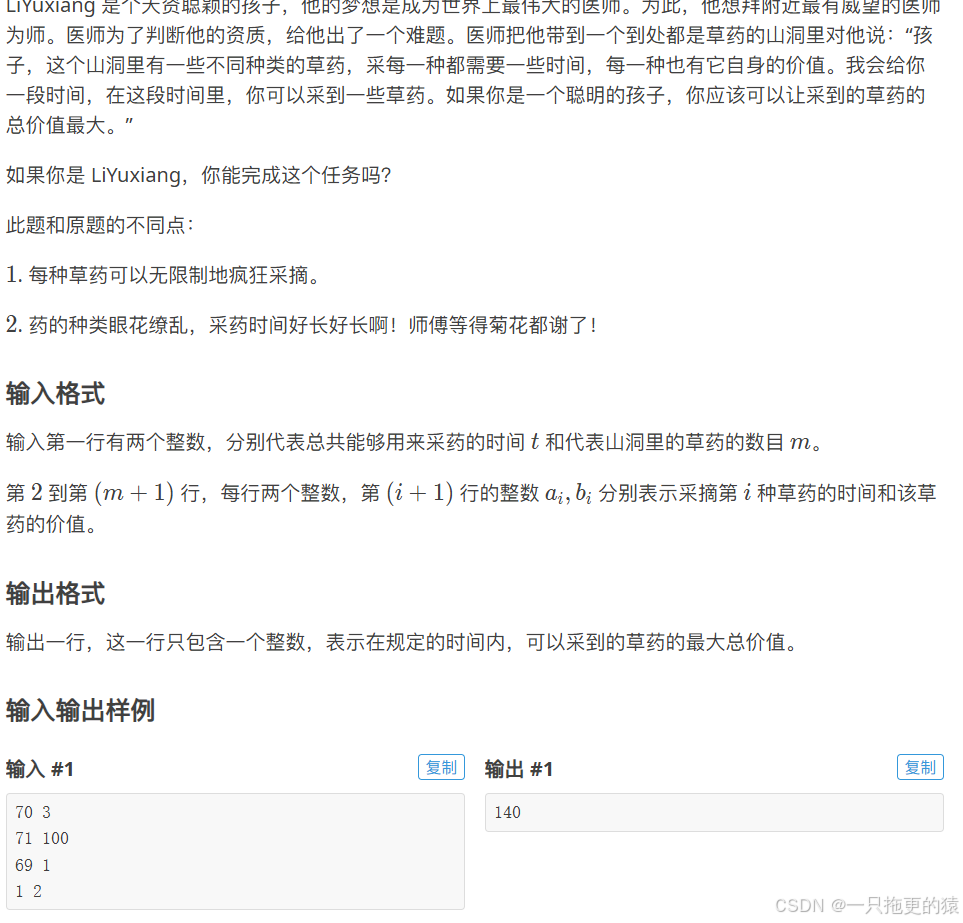
状态设计:
这种背包与01背包唯一的不同之处在于每个物品使用次数不限,所以参考01背包的dp状态:
令f[i][j]为考虑前i个物品,容量为j的背包所能装的最大总价值。
转移方程:
一种十分显然的做法是每次输入时循环添加m/w[i]次。但时间复杂度明显超了。。。
完全背包与01背包唯一的不同之处在于每个物品使用次数不限。
想想是什么限制了01背包,使其每种物品只能取一个?
![]()
真相只有一个!是它!
它保障了每次更新时如果当前位置取了物品,程序就不会再选取与当前一致的物品。
可以发现,实际上只需要将递推式改为f[i][j]=max(f[i-1][j],f[i][j-w[i]]+v[i])就能解决问题了。
而且类似的,它仍可以压缩空间为线性。
代码:
切记正序枚举!
#include <bits/stdc++.h> using namespace std; int f[114514]; int main(){ int n, m; scanf("%d%d", &n, &m); while(n--){ int w, v; scanf("%d%d", &w, &v); for(int i=w; i<=m; i++)f[i]=max(f[i], f[i - w] + v); } printf("%d\n", f[m]); return 0; }多重背包:
例题:洛谷P1776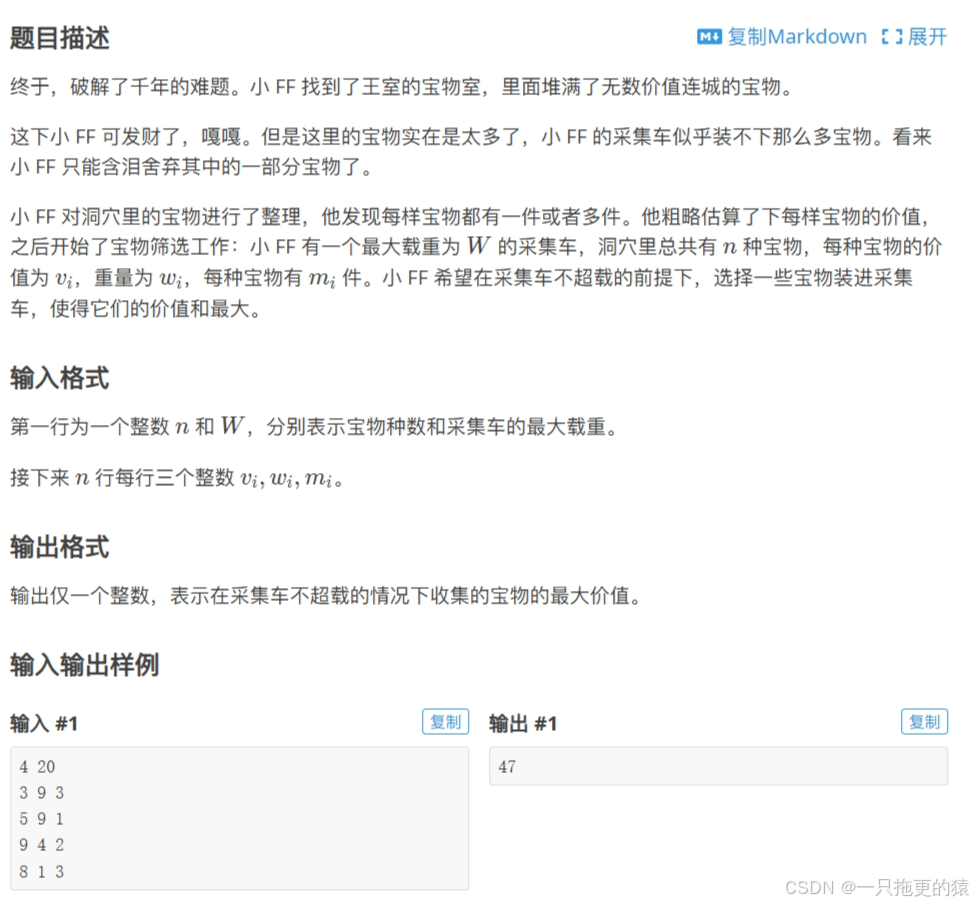
状态设计:
这种背包与01背包唯一的不同之处在于每个物品使用次数不只一次,所以参考01背包的dp状态:
令f[i][j]为考虑前i个物品,容量为j的背包所能装的最大总价值。
一种十分显然的做法是每次输入时循环添加m[i]次。但时间复杂度明显超了。。。
(没错,就是前面复制的)
优化:
二进制拆分:
遇事不决就二分。
------XXX
显然log级别的复杂度能过。
考虑二进制拆分,即将原数拆分为若干个2^n和另一个数的和的形式。
例:
5 = ( 1 + 2 ) + 2
16 = ( 1 + 2 + 4 + 8 ) + 1
31 = ( 1 + 2 + 4 + 8 + 16 )
代码:
#include <bits/stdc++.h> using namespace std; int n, w, f[40005]; void add(int a, int b){ for(int i=w; i>=b; i--) f[i]=max(f[i], f[i - b] + a); } int main(){ scanf("%d%d", &n, &w); while(n--){ int a, b, c; scanf("%d%d%d", &a, &b, &c); for(int i=0; (1<<i)<=c; i++) add(a << i, b << i), c -= 1 << i; if(c) add(a * c, b * c); } printf("%d\n", f[w]); return 0; } 单调队列:
上次关于它的一些基本知识我已经讲过了,不知道的看一看。
优化:
可能有点抽象,多重背包选取物品实际上就是一个滑动窗口。
先看朴素做法的递推式:
f[i][j]=max{
f[i-1][j],
f[i-1][j-w[i]]+v[i],
f[i-1][j-2*w[i]]+2*v[i],
……
f[i-1][j-m[i]*w[i]]+m[i]*v[i]
}
可以发现当j1同余j2且其差不超过m[i]*w[i]时,f[i][j1]与f[i][j2]有部分重合。
容易想到滑动窗口。
对于每个i我们只要动态维护w[i]个长度为m[i]的单调队列即可。其内存储f[i-1][x+k*w[i]]-k*v[i]。
代码:
#include <bits/stdc++.h> using namespace std; int f[1005][20005], v[1005], w[1005], m[1005], q[20005]; int n, V; int main() { cin >> n >> V; for (int i = 1; i <= n; i++) scanf("%d%d%d", v[i], w[i], m[i]); for (int i = 1; i <= n; i++) { for (int x = 0; x < v[i]; x++) { int a = 0, b = -1; for (int j = x; j <= V; j += v[i]) {//单调队列 if (a <= b && q[a] < j - m[i] * v[i])a++; while (a <= b && f[i - 1][q[b]] - (q[b] - x) / v[i] * w[i] < f[i - 1][j] - (j - x) / v[i] * w[i])b--; q[++b] = j; f[i][j] = f[i - 1][q[a]] + ((j - q[a]) / v[i]) * w[i]; } } } cout << f[n][V] << endl; return 0; } 