归并排序时间复杂度O(NlongN),空间复杂度O(N),是一种稳定的排序,其次可以用来做外排序算法,即对磁盘(文件)上的数据进行排序。
目录
一、有序数组排序
要理解归并排序的核心逻辑我们得先看懂下面一个题:

刚接触这个题的时候,大家可能会想把他俩写到一个数组里面然后再写一个排序算法,这是一个比较容易想到也是比较蛮力的一种方法,但是这里有一个特点这两个数组是有序的。所以有一个很巧妙的方法。
使用两个变量分别记录他们的下标,并从零下标开始,比较他们下标对应下的值把小的那个先放进去新数组里面,然后把他的下标移到下一位。然后重复进行该操作,直到把其中的一个遍历完。
当然此时还没有完全排完序,当其中一组遍历完后,还有另一组剩余的的元素没有放在新数组内,因为无法确定那一组会先遍历完所以我们俩组都需要检查一遍,检查他们的下标并把剩余元素放在新数组内。
#include<stdio.h> #include<stdlib.h> #include<assert.h> int main() { int ar1[] = { 1,2,3,4 }; int ar2[] = { 3,4,5,6,7 }; int sz1 = sizeof(ar1)/sizeof(int), sz2 = sizeof(ar2) / sizeof(int); int* arr = (int*)malloc(sizeof(int) * (sz1 + sz2)); assert(arr); int i = 0, j = 0, t = 0; while (i < sz1 && j < sz2) { if (ar1[i] < ar2[j]) arr[t++] = ar1[i++]; else arr[t++] = ar2[j++]; } while (i < sz1) arr[t++] = ar1[i++]; while (j < sz2) arr[t++] = ar2[j++]; for (int i = 0; i < sz1 + sz2; i++) printf("%d ", arr[i]); return 0; }二、排序思路
通过理解上面那个题,那么对于一个乱序的数组,我们可以把一分为二,先让两个小数组有序然后再用上面的方法合并。那么如何让这两个小数组有序呢,同样的可以把他们分别再拆开,变成四个小组,然后继续一直往下拆,直到拆到只有一个元素,那么它必然是有序的,最后进行进行一一合并,这整个的思路有点像二叉树的后续遍历。
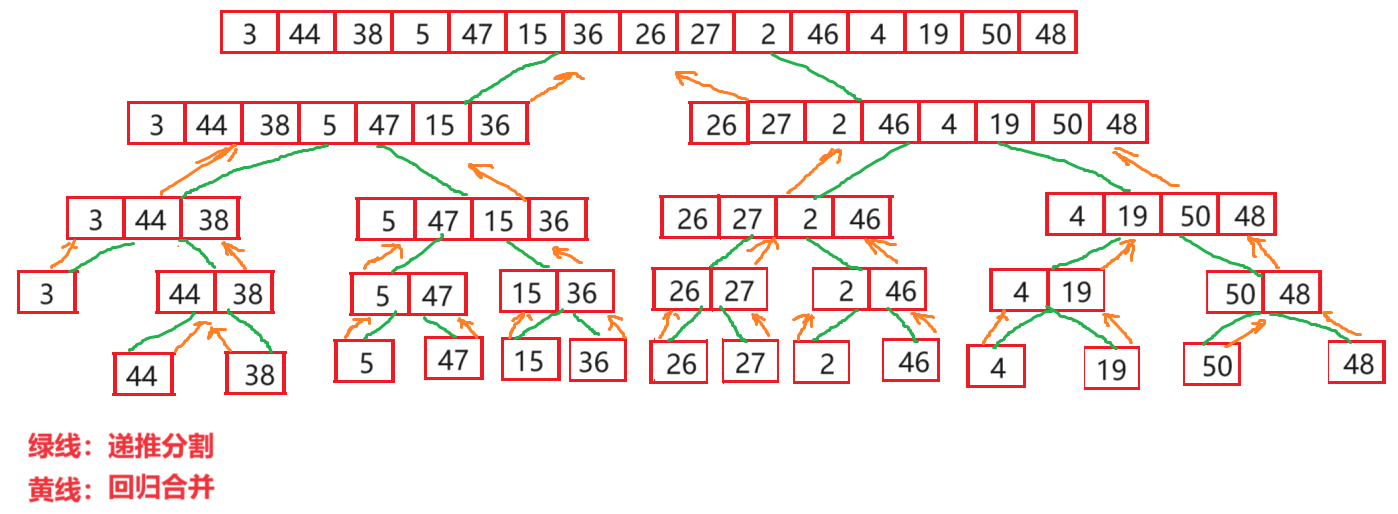
动图:
三、递归实现
在分析的过程中,我们就可以感受到使用递归可以很好的解决这个问题。在做分割的时候,最好是选择从中间位置开始,这样避免的递归深度太深。在处理递归问题的时候还要注意一个点,就是递归的结束条件,这里递归什么时候结束呢?通过上面的分析当数组只分割成单个元素的时候它必然是有序的,那么递归结束条件就是当分割的小数组只有一个元素的时候返回。
代码示例:
void _MergeSort(int* arr, int* tmp, int left, int right) { if (left >= right) return; int key = (left + right) / 2; int begin1 = left, end1 = key; int begin2 = key + 1, end2 = right; _MergeSort(arr, tmp, begin1, end1); _MergeSort(arr, tmp, begin2, end2); int i = left; while (begin1 <= end1 && begin2 <= end2) { if (arr[begin1] < arr[begin2]) tmp[i++] = arr[begin1++]; else tmp[i++] = arr[begin2++]; } while (begin1 <= end1) tmp[i++] = arr[begin1++]; while (begin2 <= end2) tmp[i++] = arr[begin2++]; memcpy(arr + left, tmp + left, sizeof(int) * (right - left + 1)); } void MergeSort(int* arr, int size)//归并排序——递归 { int* tmp = (int*)malloc(sizeof(int) * size); assert(tmp); _MergeSort(arr, tmp, 0, size - 1); free(tmp); }四、非递归实现
把递归转为非递归可以防止函数栈针开的太多导致栈溢出。在把递归转为非递归时第一想到的应该是使用栈结构来辅助完成。但是对于这个排序使用栈来实现非递归还是比较复杂,也根本用不着。
思路:
gap:表示分割的每个小数组中储存的元素个数。
size:表示整个大数的长度
首先我们仿照广度优先的思想去合并,因为刚开始只有单个元素自己作为一个数组(即gap=1)的时候才有序,所以从最后一层开始两两合并成一个,那么接下来gap=2的小数组就变得有序,合并完gap=2的的数组后,同理gap=4的小数组变得有序,对它们进行两两合并,直到gap>=size。

代码示例:
void MergeSortNoF(int* arr, int sz) { int* tmp = (int*)malloc(sizeof(int) * sz); assert(tmp); int gap = 1; while (gap < sz) { for (int i = 0; i < sz; i += gap * 2) { int j = i; int begin1 = i, end1 = i + gap - 1; int begin2 = i + gap, end2 = i + 2 * gap - 1; if (begin2 >= sz) break; if (end2 >= sz) end2 = sz - 1; while (begin1 <= end1 && begin2 <= end2) { if (arr[begin1] <= arr[begin2]) tmp[j++] = arr[begin1++]; else tmp[j++] = arr[begin2++]; } while (begin1 <= end1) tmp[j++] = arr[begin1++]; while (begin2 <= end2) tmp[j++] = arr[begin2++]; memmove(arr + i, tmp + i, sizeof(int) * (end2 - i + 1)); } gap*=2; } }细节:
无论是递归还是非递归都需要开辟一块空间tmp来储存合并后的元素,最后把tmp上的数据拷贝给原数组,使用memmove函数比较便捷。
区间越界问题:
(1)、[begin1, end1] [begin2, end2]
(2)、[begin1, end1] [begin2, end2]
(3)、[begin1, end1] [begin2, end2]
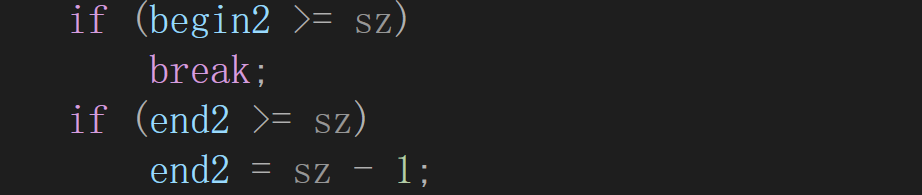
以上红色表示越界,这是越界可能出现的所有情况,观察发现出现(2),(3)种情况的时候并不需要做合并,直接break;怎么写条件呢?因为end1越界begin2一定越界,所有用一个if(begin2>=sz)就可以表示(2),(3)种情况。
至于第一种情况,我们还是要合并的但需要调整end2为sz-1,所以有一下代码: