详解数据结构之二叉树(二叉链，使用递归)

详解数据结构之二叉树(二叉链，使用递归实现)

二叉链

二叉链，二叉树的链式结构，其中数据域data存放节点的值，指针域left和right分别存放左孩子节点的地址、右孩子节点的地址。

typedef int BinaryTDataType; typedef struct BinaryTree { 	BinaryTDataType data; 	struct BinaryTree* left;//指向当前节点左孩子节点的指针 	struct BinaryTree* right;//指向当前节点右孩子节点的指针 }BTree; 

创建二叉树

由于二叉树的创建没有过多的规则限定，我们想如何创建就如何创建，所以实现二叉树的创建函数是没有意义的，这里实现一颗二叉树。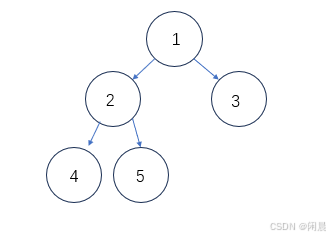

//创建节点 BTree* BtreeCreat(BinaryTDataType x) { 	BTree* node = (BTree*)malloc(sizeof(BTree)); 	if (node == NULL) 	{ 		perror("malloc"); 		exit(1); 	} 	node->data = x; 	node->left = NULL; 	node->right = NULL; 	return node; } //创建二叉树 BTree* CreatBTree() { 	BTree* node1 = BtreeCreat(1); 	BTree* node2 = BtreeCreat(2); 	BTree* node3 = BtreeCreat(3); 	BTree* node4 = BtreeCreat(4); 	BTree* node5 = BtreeCreat(5);  	node1->left = node2; 	node1->right = node3; 	node2->left = node4; 	node2->right = node5; 	return node1; } 

前序遍历

前序遍历，是一种使用遍历二叉树每一个节点的方法，主要遍历方法为先遍历根节点，然后遍历左子树，最后遍历右子树，简称：根左右。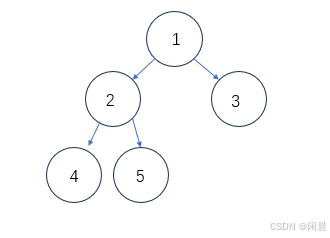

如图现在使用前序遍历打印二叉树的每一个节点，根据前序遍历规则，遍历以上二叉树的结果应为：1-2-4-5-3

更具代码，进入函数先打印了根节点对应的值，然后递归左子树，待根节点的左子树递归完后，然后递归根节点的右子树。

void PreorderTraversal(BTree* root) { 	if (root == NULL) 	{ 		return; 	} 	printf("%d ", root->data); 	PreorderTraversal(root->left); 	PreorderTraversal(root->right); } 

前序遍历的步骤：

1、打印根节点的值为1。

2、递归左子树。

3、打印根节点1的左孩子节点的值为2.

4、根节点的左孩子节点还有左孩子节点继续递归

5、打印节点2的左孩子节点的值为4

6、递归节点4的左孩子节点，判断为空指针，返回空，销毁该函数栈帧。

7、然后递归节点4的右孩子节点，判断为空指针，返回空，销毁该函数栈帧。

8、回到节点2开辟的函数栈帧，它的左孩子节点递归完后，递归它的右孩子节点。

9、打印节点2的右孩子节点值为5，然后递归5的左孩子节点和右孩子节点。

10、递归完节点5后销毁该函数，回归到节点2，此时节点2的代码执行完成，销毁该函数。

11、根节点的左子树递归完成后，进入根节点的右子树。

12、 打印节点3的值后，进入节点3的左子树，返回空，然后递归节点3的右子树，返回空。

13、节点3的函数执行完后销毁，回到根节点的函数，此时根节点的函数执行完毕，销毁该函数，递归完成。

后文的中序遍历以及后续遍历思路与前序遍历一致。

中序遍历

中序遍历，先遍历根节点的左子树，然后打印根节点，最后遍历根节点的右子树，简称：左根右。

根据上图使用中序遍历打印节点的顺序为：4-2-5-1-3

void InorderTraversal(BTree* root) { 	if (root == NULL) 	{ 		return; 	} 	InorderTraversal(root->left); 	printf("%d ", root->data); 	InorderTraversal(root->right); } 

后序遍历

后序遍历，先遍历根节点的左子树，然后遍历根节点的右子树，最后大于根节点的值，简称：左右根。

根据上图使用后序遍历打印节点的顺序为：4-5-2-3-1

void PostorderTraversal(BTree* root) { 	if (root == NULL) 	{ 		return; 	} 	PostorderTraversal(root->left); 	PostorderTraversal(root->right); 	printf("%d ", root->data); } 

层序遍历

层序遍历是指根节点考试遍历二叉树的值，根节点为第一层，打印它的值，然后就是打印第二层、第三层以此类推，从上至下，从左至右依次打印节点的值。如下图，使用层序遍历打印的结果为：1-2-3-4-5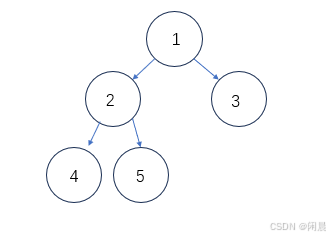

使用借组队列的数据结构实现，队列的特点是先将先出，后进后出。首先将根节点放入队列，然后取队顶数据打印出来，然后Pop队顶数据，接着将根节点的左右孩子节点放入队列以此类推，最后在队列里放入节点2的左右孩子。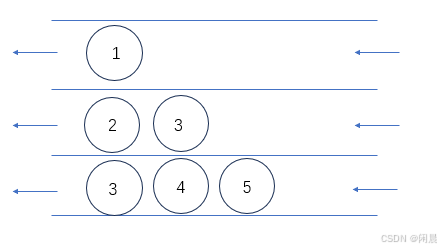

)

void LevelOrder(BTree* root) {  	Queue q; 	QueueInit(&q); 	QueuePush(&q, root); 	while (q.size) 	{ 		BTree* node = QueueFront(&q); 		printf("%d ", node->data); 		QueuePop(&q); 		if (node->left) 		{ 			QueuePush(&q, node->left); 		} 		if (node->left) 		{ 			QueuePush(&q, node->right); 		} 	} 	QueueDestory(&q); 	printf("\n"); } 

功能实现

//二叉树节点个数 int BTreeSize(BTree* root); //二叉树叶子节点个数 int BTreeLeafSize(BTree* root); //二叉树的第k层节点个数 int BTreeNodeSize(BTree* root, int k); //二叉树的高度 int BTreeDepth(BTree* root); //二叉树查找值为x的节点 BTree* BTreeFind(BTree* root, BinaryTDataType x); //二叉树的销毁 void BTreeDestory(BTree** root); 

二叉树节点个数

递归结束条件：root == NULL，遍历统计左子树的节点个数，然后再遍历统计右子树的节点个数。

int BTreeSize(BTree* root) { 	if (root == NULL) 	{ 		return 0; 	} 	return BTreeSize(root->left) + BTreeSize(root->right) + 1; } 

二叉树叶子节点个数

寻找二叉树的叶子节点，它的左孩子指针和右孩子指针指向的均为空指针，此时该节点为叶子节点，返回1。

BTreeLeafSize(root->left)，使用这串代码遍历左子树，BTreeLeafSize(root->right)，遍历右子树

当这两个函数的返回值为空时即为叶子节点，返回1给上一层创建的函数栈帧，该函数被销毁。接受1的这层函数将它左右左右子树返回的叶子节点个数相加后返回。

int BTreeLeafSize(BTree* root) { 	if (root == NULL) 	{ 		return 0; 	} 	if (BTreeLeafSize(root->left) == NULL && BTreeLeafSize(root->right) == NULL) 	{ 		return 1; 	} 	return BTreeLeafSize(root->left) + BTreeLeafSize(root->right); } 

二叉树的第k层节点个数

寻找第k层，首先第一根节点所在的层次为第一层，函数递归的限制条件就为 root == NULL 和 k == 1，函数自己掉用自己时让每一层函数的k减1，直到遍历的左子树的节点和k或者遍历右子树的节点和k，碰见 root == NULL和k == 1时开始返回。

int BTreeNodeSize(BTree* root, int k) { 	if (root == NULL) 		return 0; 	if (k == 1) 		return 1; 	return BTreeNodeSize(root->left, k - 1) + BTreeNodeSize(root->right, k - 1);  } 

二叉树的高度

计算二叉树的高度时会遇见左子树的高度大于右子树的高度，所以在返回二叉树的高度时，需要对左子树的高度大于右子树的高度还是右子树的高度大于左子树的高度，这里使用了三目操作符进行判断函数返回值，若 left > right ，那就对left所在的这一层加1，right同理。

int BTreeDepth(BTree* root) { 	if (root == NULL) 	{ 		return 0; 	} 	int left = BTreeLeafSize(root->left); 	int right = BTreeLeafSize(root->right); 	return left > right ? left + 1 : right + 1; } 

二叉树查找值为x的节点

查找值为x的节点，函数递归的限制条件多了 x == root->data，但满足该条件时返回该节点。通过先遍历左子树的节点，然后再遍历右子树的节点。若再左子树里找到了值为x的节点，或在左子树里提前找到了对应的节点，就不需要向后递归，所以在遍历左子树节点加了一条限制 if (left)，若条件为真则说明找到了该节点，返回即可，右子树同理。

BTree* BTreeFind(BTree* root, BinaryTDataType x) { 	if (root == NULL) 		return 0; 	if (x == root->data) 		return root; 	//如果说是提前找到了，就不需要向后开辟函数栈帧 	BTree* left = BTreeFind(root->left, x); 	if (left) 		return left; 	BTree* right = BTreeFind(root->right, x); 	if (right) 		return right; 	//没有找到返回空 	return NULL;  } 

二叉树的销毁

传递节点的地址，使用二级指针接受使形参的改变可以影响到实参。二叉树销毁，需要从最后一层节点开始一个一个的销毁，同意需要遍历左子树，然后遍历右子树直到遇见叶子节点，然后开始销毁它，销毁完后创建的函数栈帧销毁，返回上一层函数栈帧。如此反复循环。

void BTreeDestory(BTree** root) { 	if (*root == NULL) 	{ 		return; 	} 	BTreeDestory(&(*root)->left); 	BTreeDestory(&(*root)->right); 	free(*root); 	*root = NULL; } 

源码

BinaryTree.h

#pragma once  #include <stdio.h> #include <stdlib.h> #include <assert.h> #include <stdbool.h>  typedef int BinaryTDataType; typedef struct BinaryTree { 	BinaryTDataType data; 	struct BinaryTree* left; 	struct BinaryTree* right; }BTree;  //前序遍历 void PreorderTraversal(BTree* root); //中序遍历 void InorderTraversal(BTree* root); //后续遍历 void PostorderTraversal(BTree* root); //二叉树节点个数 int BTreeSize(BTree* root); //二叉树叶子节点个数 int BTreeLeafSize(BTree* root); //二叉树的第k层节点个数 int BTreeNodeSize(BTree* root, int k); //二叉树的高度 int BTreeDepth(BTree* root); //二叉树查找值为x的节点 BTree* BTreeFind(BTree* root, BinaryTDataType x); //二叉树的销毁 void BTreeDestory(BTree** root); 

BinaryTree.c

#include "BinaryTree.h"  //前序遍历 void PreorderTraversal(BTree* root) { 	if (root == NULL) 	{ 		return; 	} 	printf("%d ", root->data); 	PreorderTraversal(root->left); 	PreorderTraversal(root->right); } //中序遍历 void InorderTraversal(BTree* root) { 	if (root == NULL) 	{ 		return; 	} 	InorderTraversal(root->left); 	printf("%d ", root->data); 	InorderTraversal(root->right); } //后序遍历 void PostorderTraversal(BTree* root) { 	if (root == NULL) 	{ 		return; 	} 	PostorderTraversal(root->left); 	PostorderTraversal(root->right); 	printf("%d ", root->data); } //二叉树节点个数 int BTreeSize(BTree* root) { 	if (root == NULL) 	{ 		return 0; 	} 	return BTreeSize(root->left) + BTreeSize(root->right) + 1; } //二叉树叶子节点个数 int BTreeLeafSize(BTree* root) { 	if (root == NULL) 	{ 		return 0; 	} 	if (BTreeLeafSize(root->left) == NULL && BTreeLeafSize(root->right) == NULL) 	{ 		return 1; 	} 	return BTreeLeafSize(root->left) + BTreeLeafSize(root->right); } //二叉树的高度 int BTreeDepth(BTree* root) { 	if (root == NULL) 	{ 		return 0; 	} 	int left = BTreeLeafSize(root->left); 	int right = BTreeLeafSize(root->right); 	return left > right ? left + 1 : right + 1; } //二叉树的第k层节点个数 int BTreeNodeSize(BTree* root, int k) { 	if (root == NULL) 		return 0; 	if (k == 1) 		return 1; 	return BTreeNodeSize(root->left, k - 1) + BTreeNodeSize(root->right, k - 1);  } //二叉树查找值为x的节点 BTree* BTreeFind(BTree* root, BinaryTDataType x) { 	if (root == NULL) 		return 0; 	if (x == root->data) 		return root; 	//如果说是提前找到了，就不需要向后开辟函数栈帧 	BTree* left = BTreeFind(root->left, x); 	if (left) 		return left; 	BTree* right = BTreeFind(root->right, x); 	if (right) 		return right; 	//没有找到返回空 	return NULL;  } //二叉树的销毁 void BTreeDestory(BTree** root) { 	if (*root == NULL) 	{ 		return; 	} 	BTreeDestory(&(*root)->left); 	BTreeDestory(&(*root)->right); 	free(*root); 	*root = NULL; } 

test.c

#define _CRT_SECURE_NO_WARNINGS  #include "BinaryTree.h"  //创建节点 BTree* BtreeCreat(BinaryTDataType x) { 	BTree* node = (BTree*)malloc(sizeof(BTree)); 	if (node == NULL) 	{ 		perror("malloc"); 		exit(1); 	} 	node->data = x; 	node->left = NULL; 	node->right = NULL; 	return node; }  //创建二叉树 BTree* CreatBTree() { 	BTree* node1 = BtreeCreat(1); 	BTree* node2 = BtreeCreat(2); 	BTree* node3 = BtreeCreat(3); 	BTree* node4 = BtreeCreat(4); 	BTree* node5 = BtreeCreat(5); 	BTree* node6 = BtreeCreat(6);  	node1->left = node2; 	node1->right = node3; 	node2->left = node4; 	node2->right = node5; 	return node1; }  void testTraversal() { 	BTree* node = CreatBTree(); 	PreorderTraversal(node); 	printf("\n"); 	InorderTraversal(node); 	printf("\n"); 	PostorderTraversal(node); 	printf("\n"); }  void test() { 	BTree* node = CreatBTree(); 	int size = BTreeSize(node); 	printf("%d\n", size);  	int Leafsize = BTreeLeafSize(node); 	printf("%d\n", Leafsize);  	int k = BTreeDepth(node); 	printf("%d\n", k);  	int NodeSize = BTreeNodeSize(node, 1); 	printf("%d\n", NodeSize);  	BTree* retnode = BTreeFind(node, 1); 	if (retnode) 		printf("找到了！"); 	else 		printf("没有到！");  	BTreeDestory(&node); } int main() {     test(); 	return 0; }    aversal(node); 	printf("\n"); 	PostorderTraversal(node); 	printf("\n"); }  void test() { 	BTree* node = CreatBTree(); 	int size = BTreeSize(node); 	printf("%d\n", size);  	int Leafsize = BTreeLeafSize(node); 	printf("%d\n", Leafsize);  	int k = BTreeDepth(node); 	printf("%d\n", k);  	int NodeSize = BTreeNodeSize(node, 1); 	printf("%d\n", NodeSize);  	BTree* retnode = BTreeFind(node, 1); 	if (retnode) 		printf("找到了！"); 	else 		printf("没有到！");  	BTreeDestory(&node); } int main() {     test(); 	return 0; }