阅读量:0
一、找树左下角的值
题目:
给定一个二叉树的 根节点 root,请找出该二叉树的 最底层 最左边 节点的值。
假设二叉树中至少有一个节点。
示例 1:
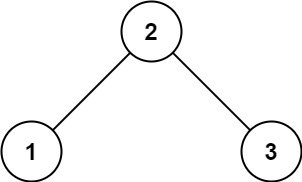
输入: root = [2,1,3] 输出: 1
示例 2:
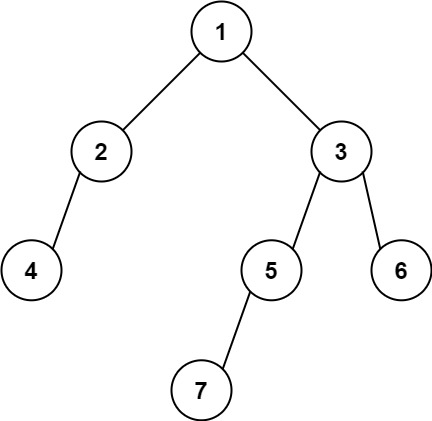
输入: [1,2,3,4,null,5,6,null,null,7] 输出: 7
思路:
该题的意思是要找到最深层的且最左端的节点,并不是找左节点, 因此容易理解错误。首先需要寻找其深度最大的叶子节点,可以采用递归的方式分别遍历其左右子树,最后输出其最深且最左端的叶子节点的值
代码:
int Deep = -1; // 全局变量,用于记录最大深度 int value = 0; // 全局变量,用于记录最底层最左边节点的值 // 主方法,返回二叉树最底层最左边节点的值 public int findBottomLeftValue(TreeNode root) { value = root.val; // 初始化value为根节点的值 findLeft(root, 0); // 调用递归方法,从根节点开始查找最左边节点 return value; // 返回最底层最左边节点的值 } // 递归方法,查找最底层最左边的节点 public void findLeft(TreeNode root, int deep) { if (root == null) return; // 如果当前节点为空,直接返回 // 如果当前节点是叶子节点,并且深度大于记录的最大深度Deep if (root.left == null && root.right == null) { if (deep > Deep) { value = root.val; // 更新最底层最左边节点的值为当前节点的值 Deep = deep; // 更新最大深度为当前深度 } } // 递归处理左子树 if (root.left != null) { deep++; // 深度加1 findLeft(root.left, deep); // 递归调用,处理左子树 deep--; // 递归结束后,深度减1,回溯到当前层 } // 递归处理右子树 if (root.right != null) { deep++; // 深度加1 findLeft(root.right, deep); // 递归调用,处理右子树 deep--; // 递归结束后,深度减1,回溯到当前层 } } 全局变量定义:
Deep和value都是全局变量,Deep初始值为-1,value初始值为0。
findBottomLeftValue 方法:
- 这是主方法,用于找到最底层最左边节点的值。
- 首先将根节点的值赋给
value。 - 然后调用
findLeft方法,传入根节点和初始的深度0。
findLeft 方法:
- 这个方法是递归地查找最底层最左边的节点。
- 如果当前节点
root为null,直接返回。 - 如果当前节点是叶子节点(即左右孩子都为
null),则判断当前深度deep是否大于Deep,如果是,则更新value为当前叶子节点的值,并更新Deep为当前深度deep。
递归左右子树:
- 如果当前节点有左子树,递归调用
findLeft方法,深度deep加一。 - 如果当前节点有右子树,同样递归调用
findLeft方法,深度deep加一。 - 每次递归结束后,深度
deep需要减一,以保证递归回溯时深度正确。
- 如果当前节点有左子树,递归调用
返回结果:
- 最终
value中存储的是最底层最左边节点的值,该值由findLeft方法更新。
- 最终
二、路径总和
题目:
给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在 根节点到叶子节点 的路径,这条路径上所有节点值相加等于目标和 targetSum 。如果存在,返回 true ;否则,返回 false 。
叶子节点 是指没有子节点的节点。
示例 1:
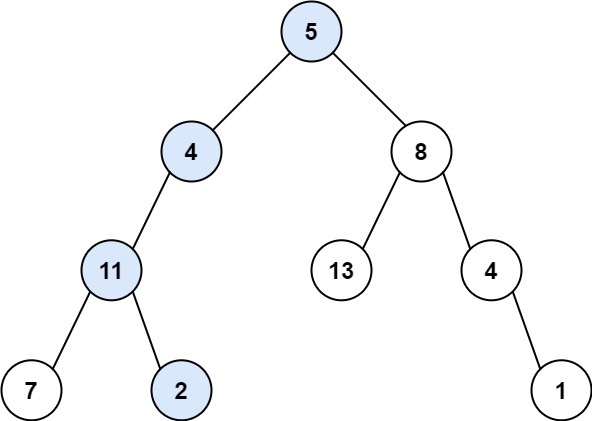
输入:root = [5,4,8,11,null,13,4,7,2,null,null,null,1], targetSum = 22 输出:true 解释:等于目标和的根节点到叶节点路径如上图所示。
示例 2:
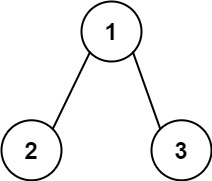
输入:root = [1,2,3], targetSum = 5 输出:false 解释:树中存在两条根节点到叶子节点的路径: (1 --> 2): 和为 3 (1 --> 3): 和为 4 不存在 sum = 5 的根节点到叶子节点的路径。
示例 3:
输入:root = [], targetSum = 0 输出:false 解释:由于树是空的,所以不存在根节点到叶子节点的路径。
思路:
初始化一个计数变量count=0,从根节点开始,每遍历一个节点让目标值减去这个节点值,最后看是否存在一个减到与count值相等的路径,有返回true,否则返回false
代码:
public boolean hasPathSum(TreeNode root, int targetSum) { // 如果根节点为空,直接返回 false if (root == null) return false; // 减去当前节点的值,更新目标和 targetSum = targetSum - root.val; // 如果当前节点是叶子节点,检查目标和是否为 0 if (root.left == null && root.right == null) { return targetSum == 0; } // 递归检查左子树是否存在满足条件的路径 if (root.left != null) { boolean left = hasPathSum(root.left, targetSum); // 如果左子树存在满足条件的路径,直接返回 true if (left) return true; } // 递归检查右子树是否存在满足条件的路径 if (root.right != null) { boolean right = hasPathSum(root.right, targetSum); // 如果右子树存在满足条件的路径,直接返回 true if (right) return true; } // 如果左右子树都不存在满足条件的路径,返回 false return false; } 今天的学习就到这里
