【数学建模】——【python】实现【最短路径】【最小生成树】【复杂网络分析】

目录

1. 最短路径问题 - 绘制城市间旅行最短路径图

题目描述：

要求：

示例数据：

python 代码实现

实现思想：

要点：

2. 最小生成树问题 - Kruskal算法绘制MST

题目描述：

要求：

示例数据：

python代码实现

实现思想：

要点：

3. 结合最短路径与最小生成树的复杂网络分析

题目描述：

python代码

实现思想： 

要点：

总结三个问题

专栏：数学建模学习笔记

上一篇：【数学建模】图与网络模型的学习

本篇是题目练习

1. 最短路径问题 - 绘制城市间旅行最短路径图

题目描述：

假设有一个包含多个城市及其之间距离的列表（或图结构），其中每个城市是图中的一个节点，城市之间的距离是边的权重。使用Dijkstra算法或Floyd-Warshall算法（视情况而定，如果图中节点数较多，推荐使用Dijkstra；如果需要求出所有点对间的最短路径，则使用Floyd-Warshall）来计算并绘制出从一个指定城市到其他所有城市的最短路径图。

要求：

（1）使用Python编程，可以利用networkx库来构建图和处理图算法。

（2）绘制结果应包含所有节点（城市）和表示最短路径的边，边的粗细或颜色可以表示距离长短。

（3）标注每条边的权重（距离）。

（4）城市的数量N通过键盘输入，城市之间的距离通过随机数生成。

示例数据：

# 城市间的距离矩阵（假设为完全图，即任意两城市间都有直接路径）  

distances = [  

    [0, 5, 10, 15],  

    [5, 0, 3, 8],  

    [10, 3, 0, 6],  

    [15, 8, 6, 0]  

]  

# 假设城市名称为 A, B, C, D

python 代码实现

import networkx as nx import matplotlib.pyplot as plt import numpy as np import matplotlib.font_manager as fm  # 设置中文字体 plt.rcParams['font.sans-serif'] = ['SimHei']  # 使用黑体 plt.rcParams['axes.unicode_minus'] = False  # 解决负号显示问题  # 输入城市数量 N = int(input("请输入城市数量: "))  # 生成随机的距离矩阵，距离在1到20之间 distances = np.random.randint(1, 21, size=(N, N)) np.fill_diagonal(distances, 0)  # 对角线距离为0  # 打印生成的距离矩阵 print("城市间的距离矩阵：") print(distances)  # 创建图并添加边 G = nx.Graph()  # 添加节点 cities = [chr(i) for i in range(65, 65 + N)]  # 使用A, B, C...表示城市 G.add_nodes_from(cities)  # 添加边及其权重 for i in range(N):     for j in range(i + 1, N):         G.add_edge(cities[i], cities[j], weight=distances[i][j])  # 输入起始城市 start_city = input(f"请输入起始城市({', '.join(cities)}): ")  # 使用Dijkstra算法计算从起始城市到所有其他城市的最短路径 lengths, paths = nx.single_source_dijkstra(G, source=start_city)  # 打印最短路径信息 print("从起始城市到其他城市的最短路径：") for target in cities:     print(f"{start_city}到{target}的最短路径为{paths[target]}，距离为{lengths[target]}")  # 获取从起始城市到最后一个城市的最短路径 end_city = cities[-1] shortest_path = paths[end_city]  # 绘制图形 pos = nx.spring_layout(G)  # 创建绘图区域 fig, ax = plt.subplots()  # 绘制所有节点 nx.draw_networkx_nodes(G, pos, node_size=500, ax=ax)  # 绘制所有边并根据权重调整颜色和宽度 edges = G.edges(data=True) edge_colors = [edge[2]['weight'] for edge in edges] edge_widths = [edge[2]['weight'] / 5 for edge in edges] edges_drawn = nx.draw_networkx_edges(G, pos, edgelist=edges, width=edge_widths, edge_color=edge_colors, edge_cmap=plt.cm.Blues, ax=ax)  # 绘制最短路径的边，使用不同颜色和宽度 path_edges = [(shortest_path[i], shortest_path[i + 1]) for i in range(len(shortest_path) - 1)] nx.draw_networkx_edges(G, pos, edgelist=path_edges, width=2, edge_color='r', ax=ax)  # 绘制节点标签 nx.draw_networkx_labels(G, pos, font_size=12, font_color='black', ax=ax)  # 绘制边标签 edge_labels = {(edge[0], edge[1]): edge[2]['weight'] for edge in edges} nx.draw_networkx_edge_labels(G, pos, edge_labels=edge_labels, ax=ax)  # 创建颜色映射条 sm = plt.cm.ScalarMappable(cmap=plt.cm.Blues, norm=plt.Normalize(vmin=min(edge_colors), vmax=max(edge_colors))) sm.set_array([])  # 仅用于显示色条 fig.colorbar(sm, ax=ax, label='距离')  # 显示图形 plt.title(f"从城市 {start_city} 到城市 {end_city} 的最短路径图") plt.axis('off') plt.show() 

请输入城市数量: 5
城市间的距离矩阵：
[[ 0  3  6  1 16]
 [18  0  9 11  3]
 [16  2  0  5 11]
 [ 9  8  1  0 17]
 [ 2  7  1  3  0]]
请输入起始城市(A, B, C, D, E): A
从起始城市到其他城市的最短路径：
A到A的最短路径为['A']，距离为0
A到B的最短路径为['A', 'B']，距离为3
A到C的最短路径为['A', 'C']，距离为6
A到D的最短路径为['A', 'D']，距离为1
A到E的最短路径为['A', 'B', 'E']，距离为6

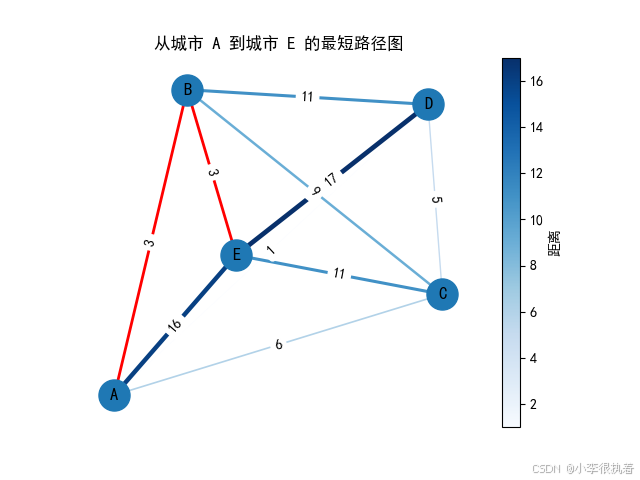
实现思想：

1. 图的表示与构建：

   • 使用图数据结构表示城市和它们之间的距离。节点表示城市，边的权重表示城市之间的距离。
   • 通过一个距离矩阵来表示各城市间的距离。

2. Dijkstra算法：

   • 用于计算从一个指定城市（源城市）到其他所有城市的最短路径。
   • 该算法适用于无负权边的图，通过贪心策略找到最短路径。

3. 可视化：

   • 使用 networkx 库构建图并计算最短路径。
   • 使用 matplotlib 库绘制图形，展示所有城市及其间的最短路径。

要点：

1. 构建随机距离矩阵：

   • 随机生成一个 N x N 的矩阵，表示 N 个城市间的距离。对角线元素为0（表示城市与自身的距离为0）。

2. 构建图并添加边：

   • 使用 networkx.Graph() 创建图对象。
   • 使用嵌套的 for 循环，将矩阵中的距离作为边的权重添加到图中。

3. 计算最短路径：

   • 使用 nx.single_source_dijkstra 函数，计算从指定源城市到所有其他城市的最短路径和路径长度。

4. 绘制图形：

   • 使用 nx.spring_layout 生成图节点的布局。
   • 使用 nx.draw 和 nx.draw_networkx_edge_labels 绘制图和边的权重。
   • 突出显示最短路径，使用不同颜色或加粗显示。

2. 最小生成树问题 - Kruskal算法绘制MST

题目描述：

给定一个无向带权图，使用Kruskal算法找到并绘制该图的最小生成树（MST）。最小生成树是图中的一个子图，它包含图中所有顶点且边的权重之和最小。

要求：

（1）使用networkx库来处理图结构。

（2）绘制结果应清晰地展示MST中的所有边和顶点，并且可以通过边的颜色或粗细来区分MST中的边与其他边。

（3）标注MST的总权重。

示例数据：

# 边列表，每个元素是一个三元组(起点, 终点, 权重)  

edges = [  

    ('A', 'B', 1),  

    ('A', 'C', 4),  

    ('A', 'D', 7),  

    ('B', 'C', 2),  

    ('B', 'D', 5),  

    ('C', 'D', 3),  

    ('C', 'E', 6),  

    ('D', 'E', 8)  

]

python代码实现

import networkx as nx import matplotlib.pyplot as plt  # 边列表，每个元素是一个三元组(起点 终点 权重) edges = [     ('A', 'B', 1),     ('A', 'C', 4),     ('A', 'D', 7),     ('B', 'C', 2),     ('B', 'D', 5),     ('C', 'D', 3),     ('C', 'E', 6),     ('D', 'E', 8) ]  # 构建图 G = nx.Graph() G.add_weighted_edges_from(edges)  # 使用Kruskal算法计算MST mst = nx.minimum_spanning_tree(G, algorithm='kruskal')  # 绘制图 pos = nx.spring_layout(G) plt.figure(figsize=(10, 8))  # 绘制原始图 nx.draw(G, pos, with_labels=True, node_size=500, node_color="lightblue", alpha=0.6) labels = nx.get_edge_attributes(G, 'weight') nx.draw_networkx_edge_labels(G, pos, edge_labels=labels)  # 绘制MST nx.draw(mst, pos, with_labels=True, node_size=500, node_color="lightgreen", edge_color="red", width=2) labels_mst = nx.get_edge_attributes(mst, 'weight') nx.draw_networkx_edge_labels(mst, pos, edge_labels=labels_mst)  # 计算MST的总权重 total_weight = mst.size(weight='weight') plt.title(f"Minimum Spanning Tree (Total Weight: {total_weight})") plt.show()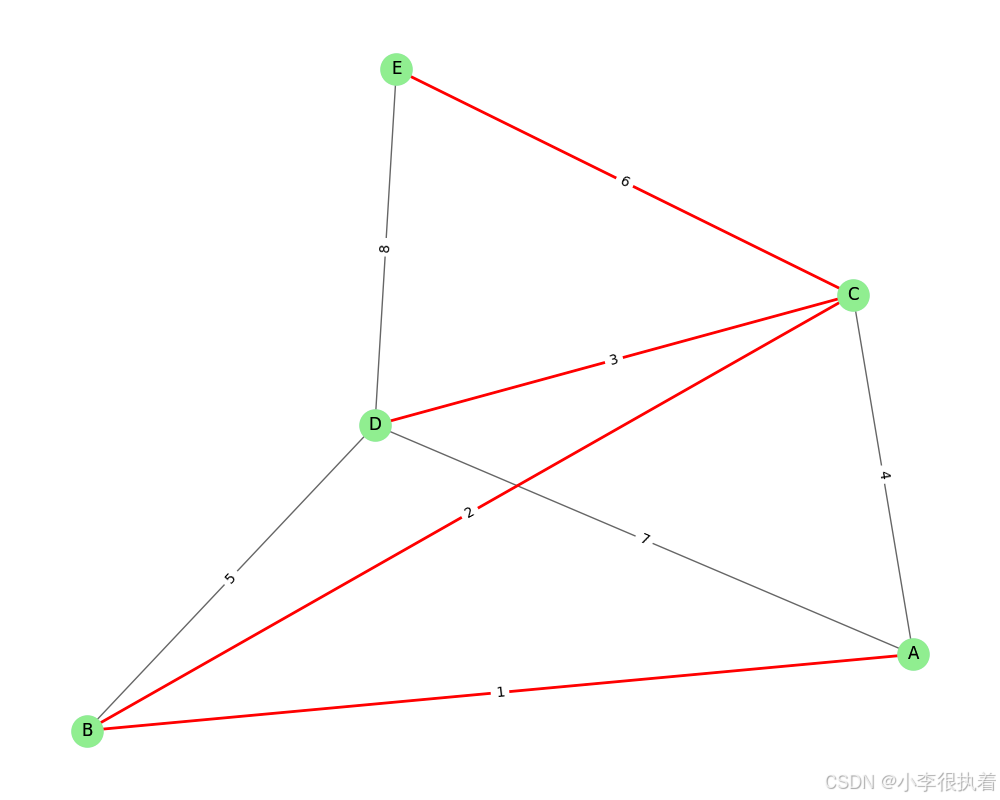 

实现思想：

1. 图的表示与构建：

   • 使用图数据结构表示城市和它们之间的距离。节点表示城市，边的权重表示城市之间的距离。
   • 使用边列表表示图，其中每个元素是一个三元组 (起点, 终点, 权重)。

2. Kruskal算法：

   • 用于找到图的最小生成树（MST）。
   • 通过贪心策略，逐步选择权重最小的边，构建权重和最小的树。

3. 可视化：

   • 使用 networkx 库构建图并计算MST。
   • 使用 matplotlib 库绘制图形，展示MST的所有节点和边。

要点：

1. 定义边列表：

   • 创建一个包含边的列表，每个元素是一个三元组 (起点, 终点, 权重)。

2. 构建图并添加边：

   • 使用 networkx.Graph() 创建图对象。
   • 使用 G.add_weighted_edges_from(edges) 添加边到图中。

3. 计算MST：

   • 使用 nx.minimum_spanning_tree(G, algorithm='kruskal') 计算图的最小生成树。

4. 绘制图形：

   • 使用 nx.spring_layout 生成图节点的布局。
   • 使用 nx.draw 和 nx.draw_networkx_edge_labels 绘制原始图及其边的权重。
   • 突出显示MST，使用不同颜色或加粗显示。

3. 结合最短路径与最小生成树的复杂网络分析

题目描述：

考虑一个大型交通网络，其中节点代表城市，边代表道路，边的权重代表道路的长度或旅行时间。首先，使用Kruskal算法找出这个网络的最小生成树（代表最基本的交通网络框架）。然后，在此MST的基础上，选择一个“核心城市”作为起点，使用Dijkstra算法找出从该城市到其他所有城市的最短路径。

要求：

（1）绘制两个图：一个是MST，另一个是以核心城市为中心的最短路径图（可以只显示与核心城市直接相连的最短路径）。

（2）MST图中应清晰区分MST边和非MST边。

（3）最短路径图中，最短路径的边可以用特殊颜色或加粗显示，并标注核心城市到各城市的最短路径长度。

示例数据：

自行设计更复杂的数据集。

python代码

import networkx as nx import matplotlib.pyplot as plt from matplotlib import font_manager  # 设置中文字体 plt.rcParams['font.sans-serif'] = ['SimHei']  # 使用黑体 plt.rcParams['axes.unicode_minus'] = False  # 解决坐标轴负号显示问题  # 边列表，每个元素是一个三元组(起点, 终点, 权重) edges = [     ('A', 'B', 1),     ('A', 'C', 4),     ('A', 'D', 7),     ('B', 'C', 2),     ('B', 'D', 5),     ('C', 'D', 3),     ('C', 'E', 6),     ('D', 'E', 8) ]  # 构建图 G = nx.Graph() G.add_weighted_edges_from(edges)  # 使用Kruskal算法计算MST mst = nx.minimum_spanning_tree(G, algorithm='kruskal')  # 使用Dijkstra算法计算最短路径 core_city = 'A' lengths, paths = nx.single_source_dijkstra(mst, source=core_city)  # 绘制MST pos = nx.spring_layout(G) plt.figure(figsize=(20, 8))  plt.subplot(121) nx.draw(G, pos, with_labels=True, node_size=500, node_color="lightblue", alpha=0.6) labels = nx.get_edge_attributes(G, 'weight') nx.draw_networkx_edge_labels(G, pos, edge_labels=labels)  nx.draw(mst, pos, with_labels=True, node_size=500, node_color="lightgreen", edge_color="red", width=2) labels_mst = nx.get_edge_attributes(mst, 'weight') nx.draw_networkx_edge_labels(mst, pos, edge_labels=labels_mst) total_weight = mst.size(weight='weight') plt.title(f"最小生成树 (总权重: {total_weight})")  # 绘制最短路径图 plt.subplot(122) nx.draw(mst, pos, with_labels=True, node_size=500, node_color="lightblue") labels_mst = nx.get_edge_attributes(mst, 'weight') nx.draw_networkx_edge_labels(mst, pos, edge_labels=labels_mst)  for target in lengths:     if target == core_city:         continue     path = paths[target]     edges_in_path = [(path[i], path[i + 1]) for i in range(len(path) - 1)]     nx.draw_networkx_edges(mst, pos, edgelist=edges_in_path, width=2, edge_color='r')     path_length = lengths[target]     plt.text(pos[path[-1]][0], pos[path[-1]][1], f"{path_length:.2f}", fontsize=12, color='red')  plt.title(f"从核心城市 {core_city} 出发的最短路径")  plt.show()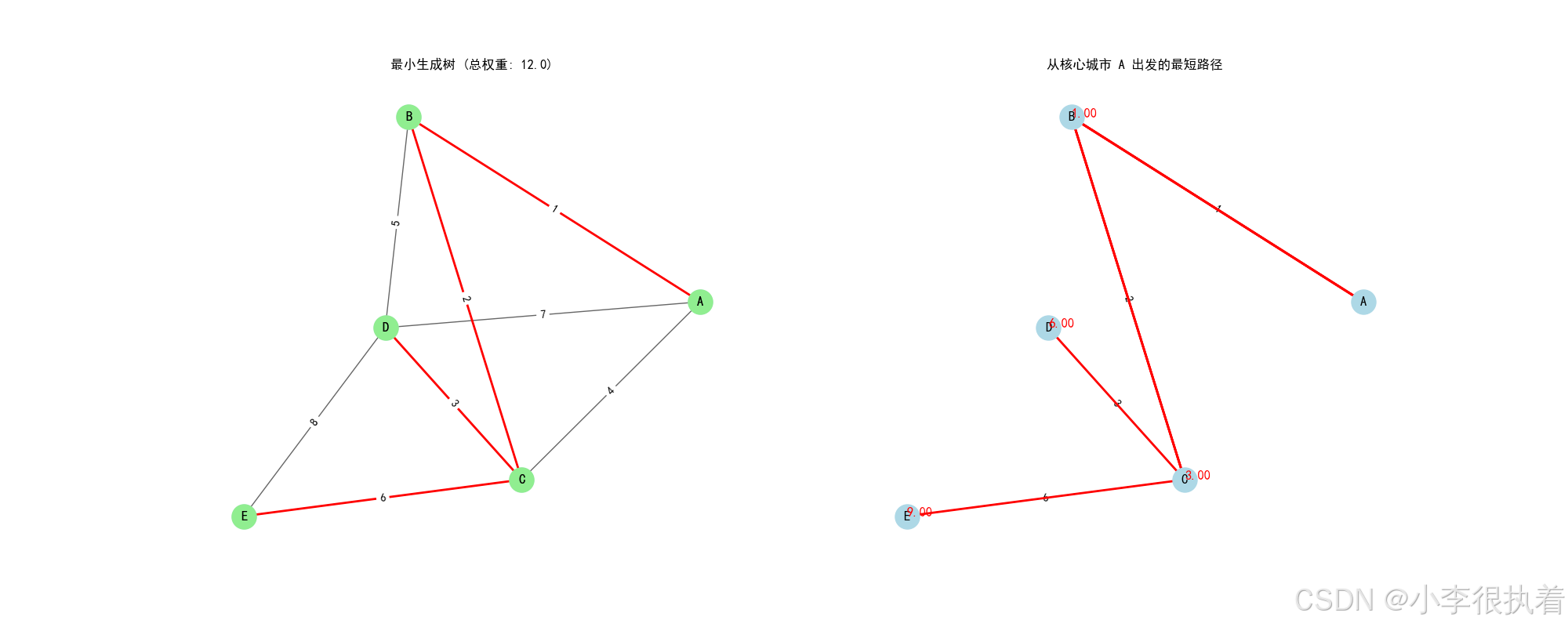 

实现思想： 

1. 图的表示与构建：

   • 使用图数据结构表示城市和它们之间的距离。节点表示城市，边的权重表示城市之间的距离。
   • 使用边列表表示图，其中每个元素是一个三元组 (起点, 终点, 权重)。

2. 计算MST：

   • 使用 Kruskal算法计算图的最小生成树（MST）。

3. 计算最短路径：

   • 在MST的基础上，使用Dijkstra算法计算核心城市到其他所有城市的最短路径。

4. 可视化：

   • 绘制两个图：一个是MST，一个是核心城市的最短路径图。
   • 使用 networkx 库构建图并计算MST和最短路径。
   • 使用 matplotlib 库绘制图形，展示MST和最短路径。

要点：

1. 定义边列表：

   • 创建一个包含边的列表，每个元素是一个三元组 (起点, 终点, 权重)。

2. 构建图并添加边：

   • 使用 networkx.Graph() 创建图对象。
   • 使用 G.add_weighted_edges_from(edges) 添加边到图中。

3. 计算MST：

   • 使用 nx.minimum_spanning_tree(G, algorithm='kruskal') 计算图的最小生成树。

4. 计算最短路径：

   • 使用 nx.single_source_dijkstra(mst, source=core_city) 在MST上计算核心城市到其他城市的最短路径。

5. 绘制图形：

   • 使用 nx.spring_layout 生成图节点的布局。
   • 使用 plt.figure 创建绘图窗口。
   • 使用 nx.draw 和 nx.draw_networkx_edge_labels 绘制MST及其边的权重。
   • 突出显示最短路径，使用不同颜色或加粗显示路径边。

总结三个问题

这三个问题分别涉及图论中的最短路径问题、最小生成树问题以及结合这两种方法的复杂网络分析。第一个问题使用Dijkstra算法计算并可视化了从一个指定城市到其他所有城市的最短路径，第二个问题使用Kruskal算法找到并绘制了一个无向带权图的最小生成树，第三个问题在最小生成树的基础上，使用Dijkstra算法计算并展示了从核心城市到其他所有城市的最短路径。每个问题都结合了图的构建、算法的应用和结果的可视化。