1、长度最小的子数组
题目描述:
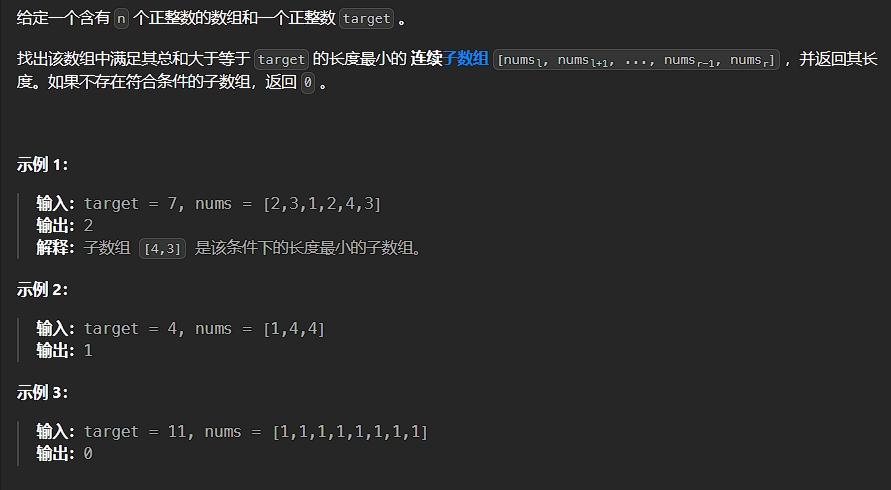
解法:
设一个 for 循环来改变指向窗口末尾的指针,再不断抛弃当前窗口内的首元素
最终确定满足条件的最小长度
class Solution { public: int minSubArrayLen(int target, vector<int>& nums) { int n = nums.size(), result = INT_MAX, sum = 0, left = 0; for(int right = 0; right < n; ++right){ sum += nums[right]; while(sum >= target){ result = min(result, right - left + 1); sum -= nums[left]; // 从 sum 中减去当前 i 指向的数值 left++; } } return result <= n ? result : 0; } };当前窗口内的元素和大于目标时,先缩小窗口大小,观测缩小后的窗口内的元素之和是否仍然满足大于目标的条件。以下 while 循环的主要作用是更新窗口起始点
while(sum >= target){ result = min(result, right - left + 1); sum -= nums[left]; // 从 sum 中减去当前 i 指向的数值 left++; }2、无重复字符的最长子串
题目描述:
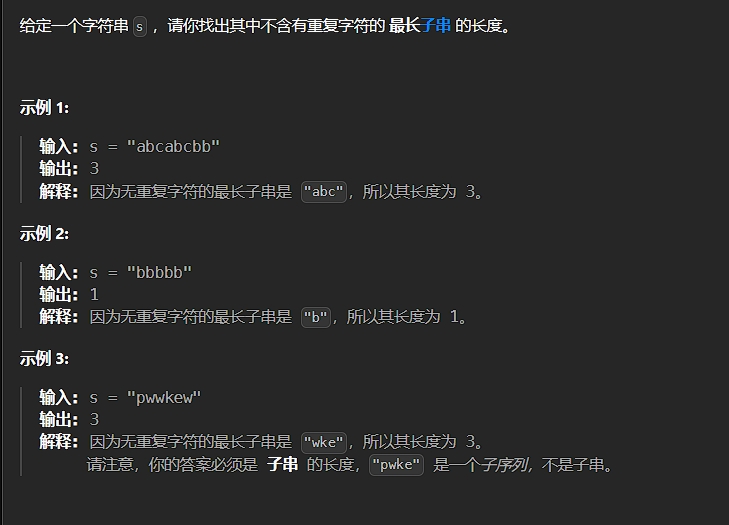
解法:
建立一个哈希表,将不重复的元素加入表中,继续向后遍历,一旦出现重复元素,删掉哈希表中最左侧的元素,继续移动窗口直至遍历完字符串
class Solution { public: int lengthOfLongestSubstring(string s) { unordered_set<char> map; int left = 0; int res = 0; if(s.size() == 0) return 0; for(int i = 0; i < s.size(); ++i){ // 遇到重复字符 while(map.find(s[i]) != map.end()){ map.erase(s[left]); left++; } res = max(res, i - left + 1); // 更新长度 map.insert(s[i]); // 向哈希表中加入该元素 } return res; } };3、有效的数独
题目描述:

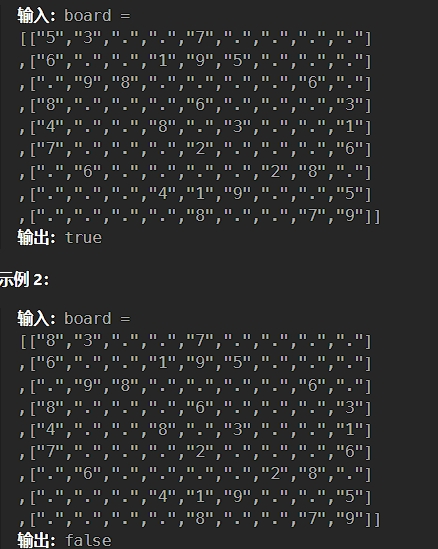
解法:
这题的解法很巧妙,大家可以去看这位老师的题解
建立3个二维数组 row[9][10]、col[9][10]、box[9][10] 分别对应行、列、3*3矩阵块,用模拟哈希表的思想来判断当前数字是否在这3个二维数组中出现过
为什么 row[9][10] 第二维是10呢?因为数字中包含9,如果设为 row[9][9] 会提醒溢出,[9]的下标最多到8,无法存储数字9
box[ j/3 + (i/3)*3 ]是最关键的地方,用来判断当前数字位于哪一个3*3矩阵块,原理是:
原有矩阵为 9*9 ,按照 x轴 可分为0、1、2三个区域,所以 j/3 就可以确定当前数字在0、1、2中的哪一个区域
同理可根据 i/3 来确定当前数字在 y 轴上的哪一个区域,选定 y轴 上的0、1、2区域后,由于 区域0 后面还有2个区域,同理1、2后面也都各有2个区域,所以使用 (i/3)*3 来确定最终块的位置
这里是先选定 j 再去细分 i 的,两者可以颠倒过来,即
box[ i/3 + (j/3)*3 ]
class Solution { public: bool isValidSudoku(vector<vector<char>>& board) { // 建立3个类似哈希表的二维数组,分别判断当前数字是否在行、列、box中出现过 int row[9][10] = {0}; int col[9][10] = {0}; int box[9][10] = {0}; for(int i = 0; i < 9; ++i){ for(int j = 0; j < 9; ++j){ if(board[i][j] == '.') continue; // 将board[i][j]中存储的数字字符转换成整数 int curNum = board[i][j] - '0'; if(row[i][curNum]) return false; // 已经在当前行出现过 if(col[j][curNum]) return false; if(box[i/3 + (j/3)*3][curNum]) return false; row[i][curNum] = 1; col[j][curNum] = 1; box[i/3 + (j/3)*3][curNum] = 1; } } return true; } };4、螺旋矩阵
题目描述:
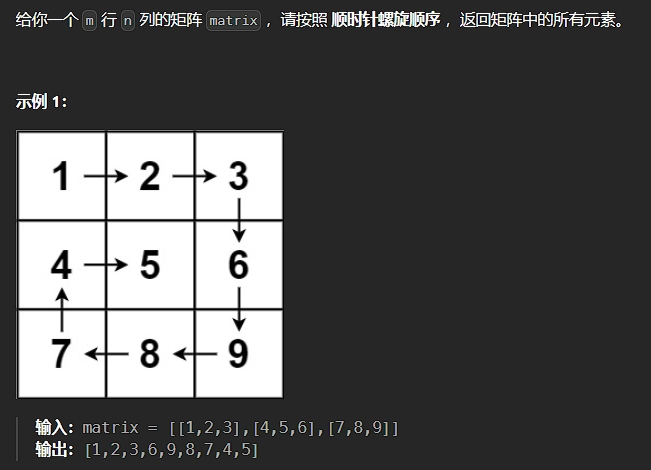
解法:
K神无敌,都说累了
class Solution { public: vector<int> spiralOrder(vector<vector<int>>& matrix) { vector<int> res; int l = 0, r = matrix[0].size() - 1, t = 0, b = matrix.size() - 1; while(true){ for(int i = l; i <= r; ++i){ res.push_back(matrix[t][i]); // 1、2、3入,5入 } if(++t > b) break; for(int i = t; i <= b; ++i){ res.push_back(matrix[i][r]); // 6、9入 } if(l > --r) break; for(int i = r; i >= l; i--){ res.push_back(matrix[b][i]); // 8、7入 } if (t > --b) break; for(int i = b; i >= t; i--){ res.push_back(matrix[i][l]); // 4入 } if (++l > r) break; } return res; } };