Pytorch深度学习实践（8）多分类任务

多分类问题

多分类问题主要是利用了Softmax分类器，数据集采用MNIST手写数据集

设计方法：

• 把每一个类别看成一个二分类的问题，分别输出10个概率

  

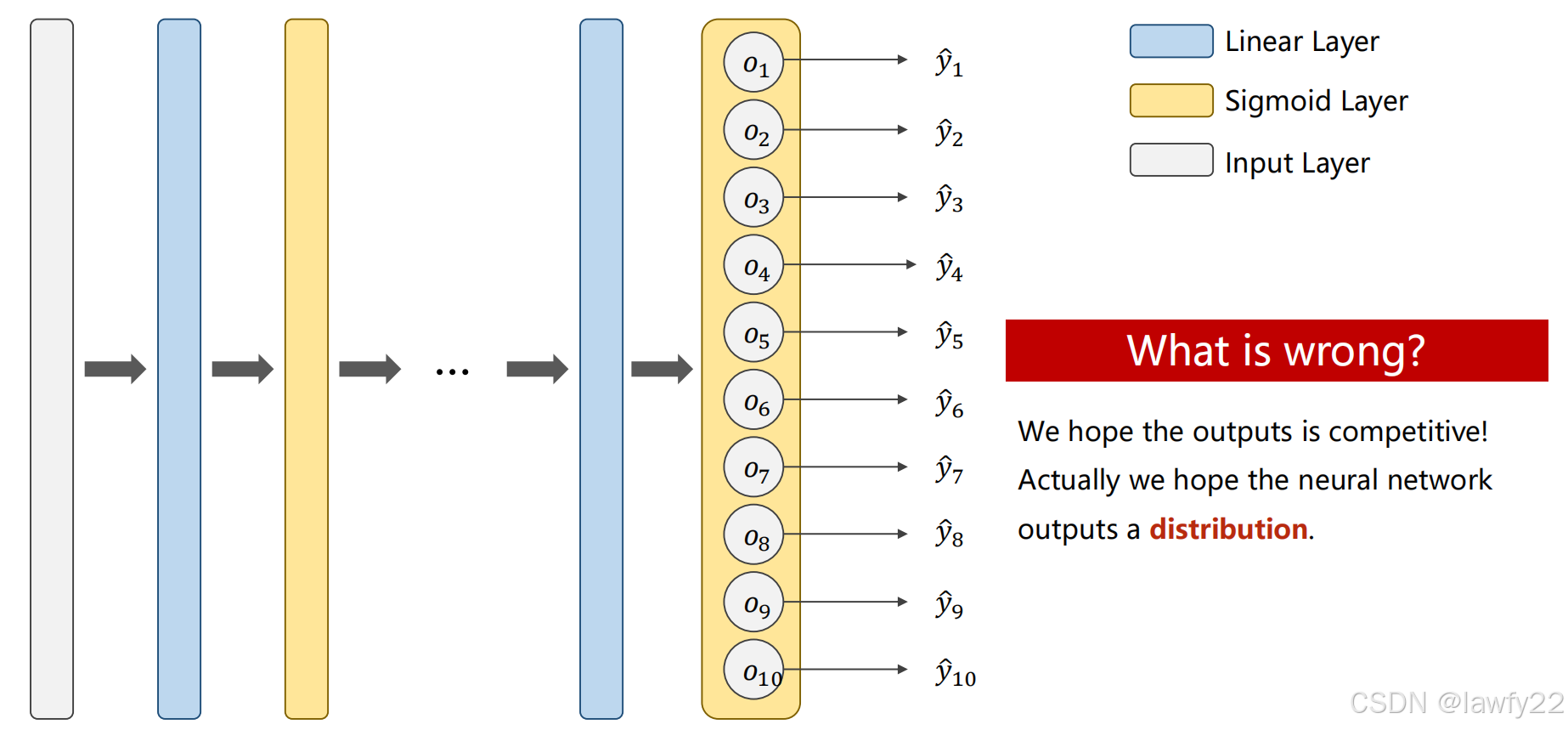
  但是这种方法存在一种问题：不存在抑制问题，即按照常规来讲，当 ${\hat{y}}_1$较大时，其他的值应该较小，换句话说，就是这10个概率相加不为1，即最终的输出结果不满足离散化分布的要求

• 引入Softmax算子，即在输出层使用softmax层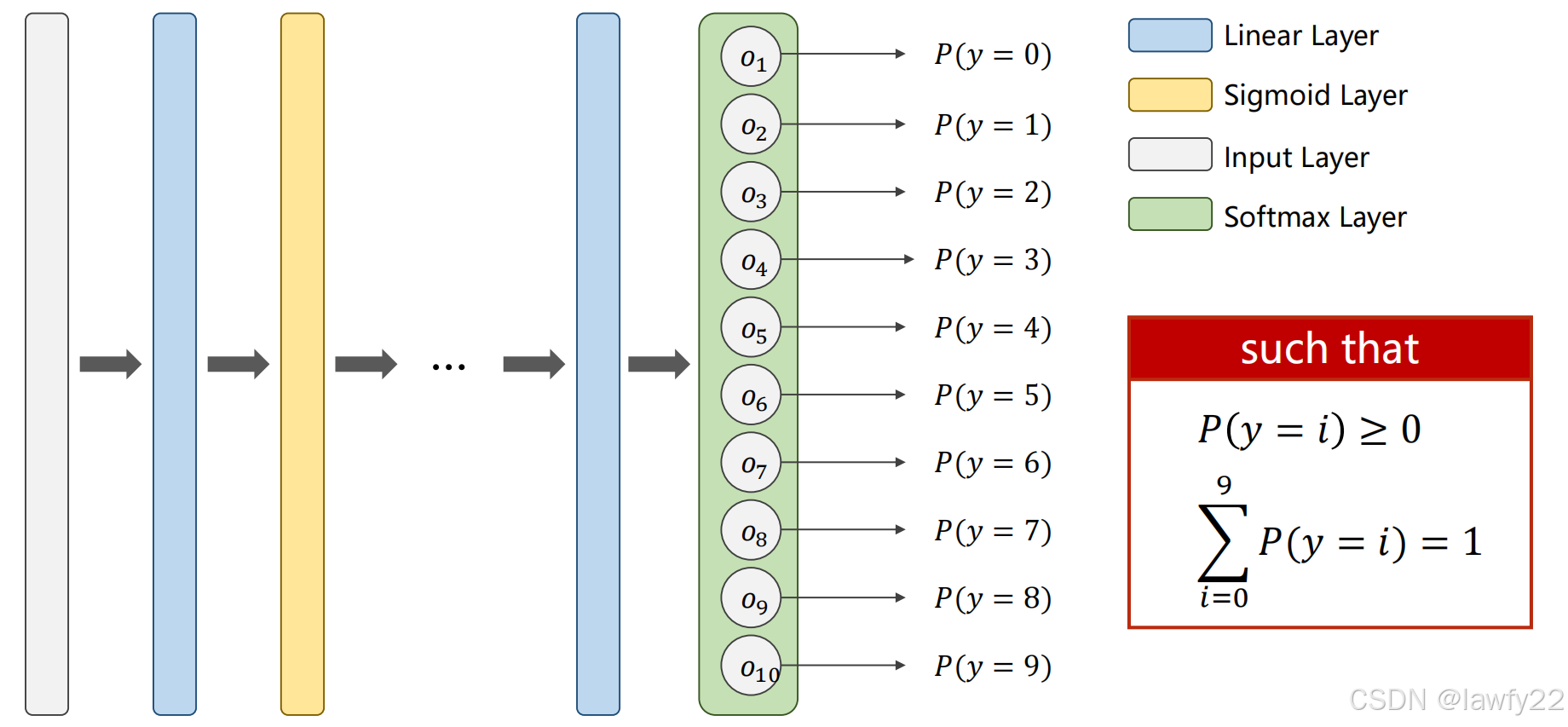
  

Softmax层

softmax函数定义：
$$P(y=i)=\frac{e^{z_i}}{{\sum }_{j=0}^{K-1}{e}^{z_j}}$$

• 首先，使用指数$e^{z_i}$，保证所有的输出都大于0
• 其次，分母中对所有的输出进行指数计算后求和，相当于对结果归一化，保证了最后10个类别的概率相加为1

损失函数

NLL损失

$$Loss(\hat{Y},Y)=-Ylog\hat{Y}$$

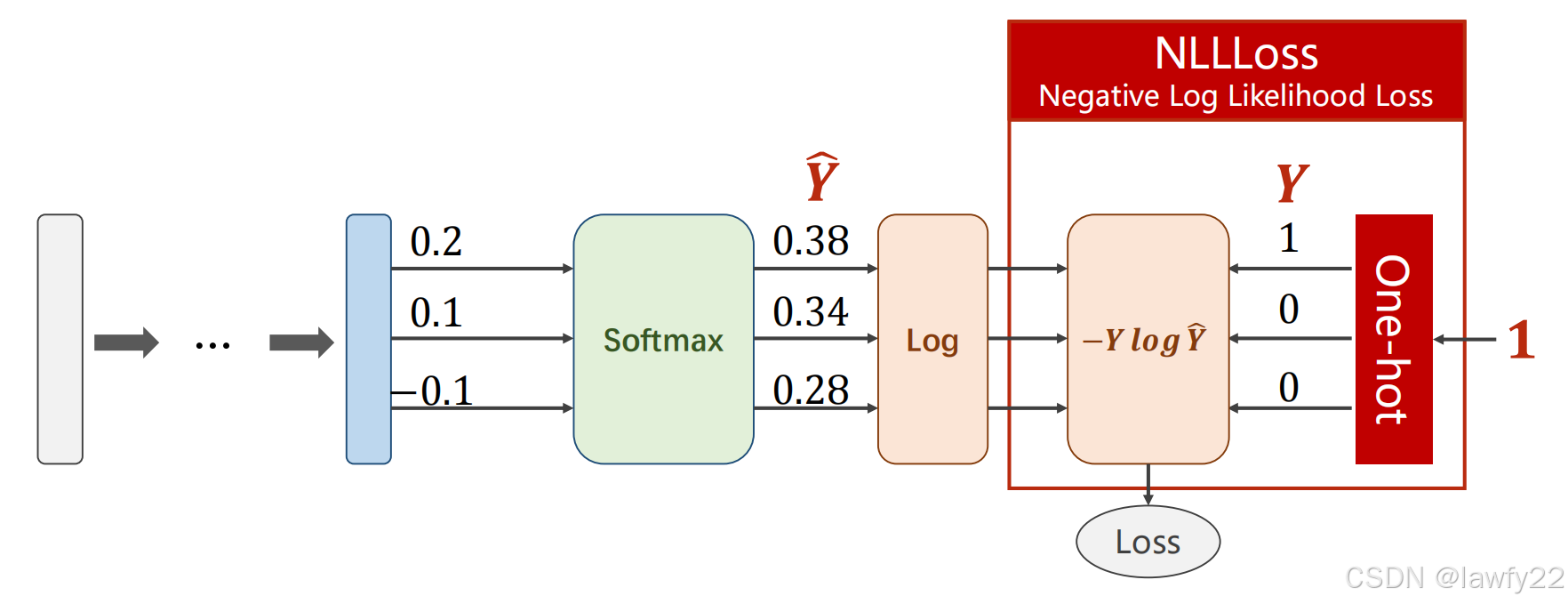
y_pred = np.exp(z) / np.exp(z).sum() loss = (-y * np.log(y_pred)).sum 

也可以直接将标签为1的类对应的$log\hat{Y}$拿出来直接做运算

交叉熵损失

交叉熵损失 = LogSoftmax + NLLLoss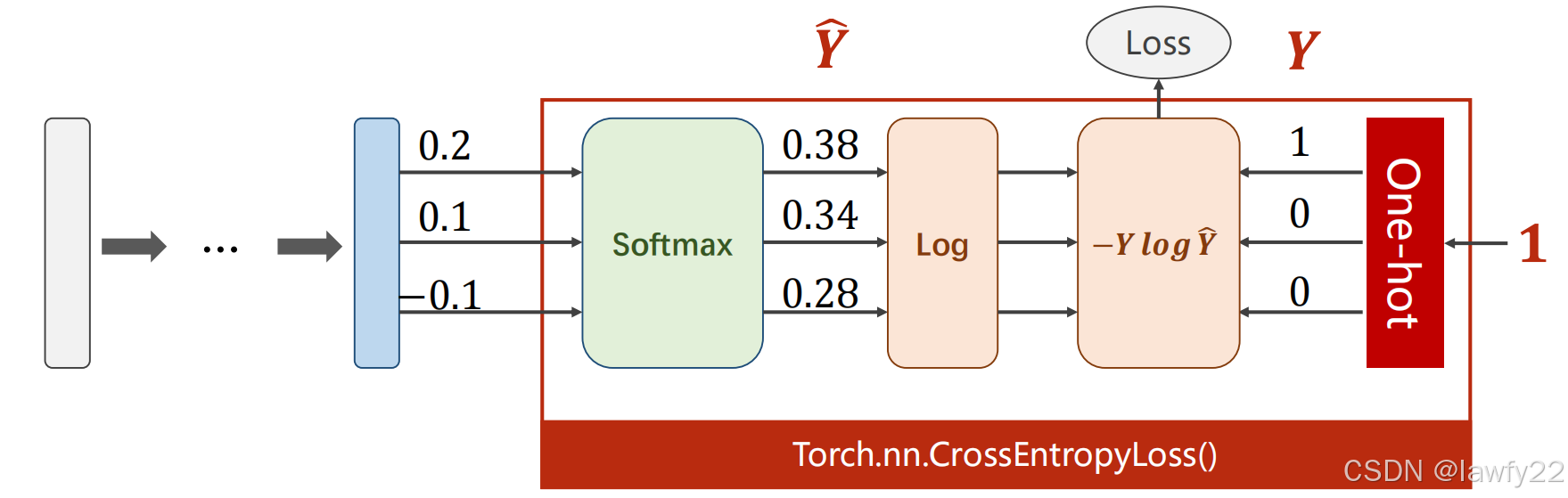

注意：

• 交叉熵损失中，神经网络的最后一层不做激活，激活函数包括在交叉熵中了
• y需要使用长整型的张量 y = torch.LongTensor([0])
• 直接调用函数使用，criterion = torch.nn.CrossEntropyLoss()

代码实现

import torch from torchvision import transforms  # 对图像进行处理 from torchvision import datasets from torch.utils.data import DataLoader import torch.nn.functional as F  # 非线性函数的包 import torch.optim as optim  # 优化 

处理数据集

要把图像数据转化为Tensor形式，因此要定义transform对象

########### 数据集处理 ########## batch_size = 64 ## 将图像转化为张量 transform = transforms.Compose([     transforms.ToTensor(),  # 使用ToTensor()方法将图像转化为张量     transforms.Normalize((0.1307, ), (0.3081, ))  # 归一化 均值-标准差 切换到01分布 ]) tran_dataset = datasets.MNIST(root='./dataset/mnist/',                               train=True,                               download=True,                               transform=transform)  # 将transform放到数据集里 直接处理  train_loader = DataLoader(tran_dataset,                           shuffle=True,                           batch_size=batch_size)  test_dataset = datasets.MNIST(root='./dataset/mnist/',                               train=False,                               download=True,                               transform=transform)  test_loader = DataLoader(test_dataset,                          shuffle=True,                          batch_size=batch_size) 

模型定义

由于线性模型的输入必须是一个向量，而图像为$28\times 28\times 1$的矩阵，因此要先把图像拉成成一个$1\times 784$的向量

这种做法会导致图像中的一些局部信息丢失

########## 模型定义 ########## ## 1×28×28 --view-> 1×784 ## 784 --> 512 --> 256 --> 128 --> 128 --> 64 -->10 class Net(torch.nn.Module):     def __init__(self):         super(Net, self).__init__()         self.l1 = torch.nn.Linear(784, 512)         self.l2 = torch.nn.Linear(512, 256)         self.l3 = torch.nn.Linear(256, 128)         self.l4 = torch.nn.Linear(128, 64)         self.l5 = torch.nn.Linear(64, 10)      def forward(self, x):         x = x.view(-1, 784)  # 图像矩阵拉伸成向量         x = F.relu(self.l1(x))         x = F.relu(self.l2(x))         x = F.relu(self.l3(x))         x = F.relu(self.l4(x))         x = self.l5(x)  # 最后一层不需要激活 sigmoid包含在cross entropy里         return x  model = Net() 

注意最后一层不需要添加softmax，因为损失函数使用的cross entorpy已经包含softmax函数

损失函数和优化器设置

由于模型比较复杂，所以使用动量梯度下降方法，参数设置为0.5

########## 损失函数和优化器设置 ########## criterion = torch.nn.CrossEntropyLoss() ## momentum指带冲量的梯度下降 optimizer = optim.SGD(model.parameters(), lr = 0.01, momentum=0.5) 

动量梯度下降（Gradient descent with momentum）

动量梯度下降方法是对小批量mini-batch的一种优化，可以有效地减少收敛过程中摆动幅度的大小，提高效率

动量梯度下降的过程类似于一个带有质量的小球在函数曲线上向下滚落，当小求滚落在最低点后，由于惯性还会继续上升一段距离，然后再滚落回来，再经最低点上去…最终小球停留在最低点处。而且由于小球具有惯性这一特点，当函数曲面比较复杂陡峭时，它便可以越过这些而尽快达到最低点

动量梯度下降每次更新参数时，对各个mini-batch求得的梯度$\nabla W$ ，$\nabla b$使用指数加权平均得到$V_{\nabla w}$和$V_{\nabla b}$，即通过历史数据来更新当前参数，从而得到更新公式：
$$V_{\nabla W_{n+1}}=\beta V_{\nabla W_n}+(1-\beta )\nabla W_n$$

$$V_{\nabla b_{n+1}}=\beta V_{\nabla b_n}+(1-\beta )\nabla b_n$$

模型训练

将训练阶段封装成一个函数

########## 模型训练 ########## def train(epoch):     running_loss = 0.0     for batch_idx, data in enumerate(train_loader, 0):         inputs, labels = data         optimizer.zero_grad()  # 优化器清零          ## forward         outputs = model(inputs)         loss = criterion(outputs, labels)         ## backward         loss.backward()         ## updata         optimizer.step()          running_loss += loss.item()         if batch_idx % 300 == 299:  # 每300轮 输出一次损失             print('[%d %5d] loss: %.3f' % (epoch + 1, batch_idx+1, running_loss / 300))             running_loss = 0.0 

模型测试

将模型的测试封装成一个函数，且每训练一轮，测试一次

def test():     correct = 0     total = 0     with torch.no_grad():  # 以下代码不会计算梯度         for data in test_loader:             images, labels = data             outputs = model(images)  # 得到十个概率             ## 返回 最大值和最大值下标 我们只需要最大值下标即可             _, predicted = torch.max(outputs.data, dim=1)  # 取最大值             total += labels.size(0)             correct += (predicted == labels).sum().item()     print('Accuracy on test set: %d %%' % (100 * correct / total)) 

主函数

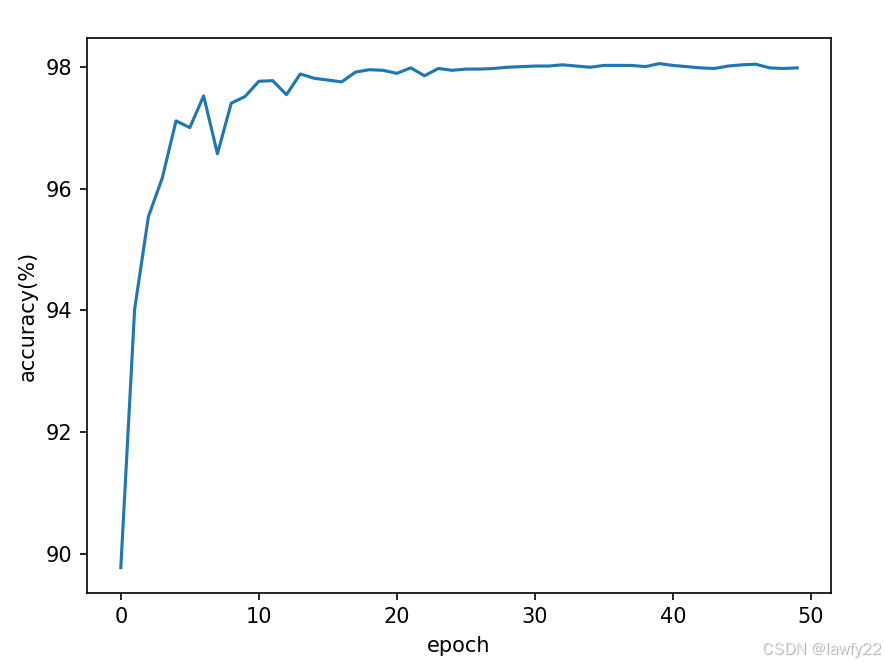
########### main ########## if __name__ == '__main__':     accuracy_history = []     epoch_history = []     for epoch in range(50):         train(epoch)         accuracy = test()         accuracy_history.append(accuracy)         epoch_history.append(epoch)     plt.plot(epoch_history, accuracy_history)     plt.xlabel('epoch')     plt.ylabel('accuracy')     plt.show() 

完整代码

import torch import matplotlib.pyplot as plt from torchvision import transforms  # 对图像进行处理 from torchvision import datasets from torch.utils.data import DataLoader import torch.nn.functional as F  # 非线性函数的包 import torch.optim as optim  # 优化  ########### 数据集处理 ########## batch_size = 64 ## 将图像转化为张量 transform = transforms.Compose([     transforms.ToTensor(),  # 使用ToTensor()方法将图像转化为张量     transforms.Normalize((0.1307, ), (0.3081, ))  # 归一化 均值-标准差 切换到01分布 ]) tran_dataset = datasets.MNIST(root='./dataset/mnist/',                               train=True,                               download=False,                               transform=transform)  # 将transform放到数据集里 直接处理  train_loader = DataLoader(tran_dataset,                           shuffle=True,                           batch_size=batch_size)  test_dataset = datasets.MNIST(root='./dataset/mnist/',                               train=False,                               download=False,                               transform=transform)  test_loader = DataLoader(test_dataset,                          shuffle=True,                          batch_size=batch_size)  ########## 模型定义 ########## ## 1×28×28 --view-> 1×784 ## 784 --> 512 --> 256 --> 128 --> 128 --> 64 -->10 class Net(torch.nn.Module):     def __init__(self):         super(Net, self).__init__()         self.l1 = torch.nn.Linear(784, 512)         self.l2 = torch.nn.Linear(512, 256)         self.l3 = torch.nn.Linear(256, 128)         self.l4 = torch.nn.Linear(128, 64)         self.l5 = torch.nn.Linear(64, 10)      def forward(self, x):         x = x.view(-1, 784)  # 图像矩阵拉伸成向量         x = F.relu(self.l1(x))         x = F.relu(self.l2(x))         x = F.relu(self.l3(x))         x = F.relu(self.l4(x))         x = self.l5(x)  # 最后一层不需要激活 sigmoid包含在cross entropy里         return x  model = Net()  ########## 损失函数和优化器设置 ########## criterion = torch.nn.CrossEntropyLoss() ## momentum指带冲量的梯度下降 optimizer = optim.SGD(model.parameters(), lr = 0.01, momentum=0.5)  ########## 模型训练 ########## def train(epoch):     running_loss = 0.0     for batch_idx, data in enumerate(train_loader, 0):         inputs, labels = data         optimizer.zero_grad()  # 优化器清零          ## forward         outputs = model(inputs)         loss = criterion(outputs, labels)         ## backward         loss.backward()         ## updata         optimizer.step()          running_loss += loss.item()         if batch_idx % 300 == 299:  # 每300轮 输出一次损失             print('[%d %5d] loss: %.3f' % (epoch + 1, batch_idx+1, running_loss / 300))             running_loss = 0.0 ########## 模型测试 ########## def test():     correct = 0     total = 0     with torch.no_grad():  # 以下代码不会计算梯度         for data in test_loader:             images, labels = data             outputs = model(images)  # 得到十个概率             ## 返回 最大值和最大值下标 我们只需要最大值下标即可             _, predicted = torch.max(outputs.data, dim=1)  # 取最大值             total += labels.size(0)             correct += (predicted == labels).sum().item()     print('Accuracy on test set: %d %%' % (100 * correct / total))     return 100*correct / total  ########### main ########## if __name__ == '__main__':     accuracy_history = []     epoch_history = []     for epoch in range(50):         train(epoch)         accuracy = test()         accuracy_history.append(accuracy)         epoch_history.append(epoch)     plt.plot(epoch_history, accuracy_history)     plt.xlabel('epoch')     plt.ylabel('accuracy(%)')     plt.show()