108. 冗余连接
时间限制:1.000S 空间限制:256MB
题目描述
树可以看成是一个图(拥有 n 个节点和 n - 1 条边的连通无环无向图)。
现给定一个拥有 n 个节点(节点标号是从 1 到 n)和 n 条边的连通无向图,请找出一条可以删除的边,删除后图可以变成一棵树。
输入描述
第一行包含一个整数 N,表示图的节点个数和边的个数。
后续 N 行,每行包含两个整数 s 和 t,表示图中 s 和 t 之间有一条边。
输出描述
输出一条可以删除的边。如果有多个答案,请删除标准输入中最后出现的那条边。
输入示例
3 1 2 2 3 1 3输出示例
1 3提示信息
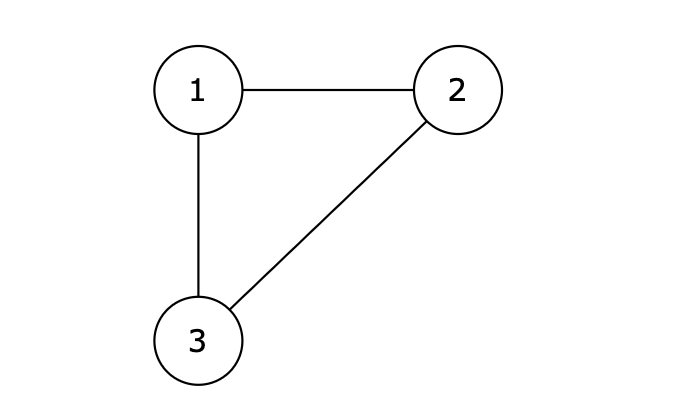
图中的 1 2,2 3,1 3 等三条边在删除后都能使原图变为一棵合法的树。但是 1 3 由于是标准输出里最后出现的那条边,所以输出结果为 1 3
数据范围:
1 <= N <= 1000.
思路:
这道题目也是并查集基础题目。
从前向后遍历每一条边(因为优先让前面的边连上),边的两个节点如果不在同一个集合,就加入集合(即:同一个根节点)。
节点A 和节点 B 不在同一个集合,那么就可以将两个节点连在一起。
如果边的两个节点已经出现在同一个集合里,说明着边的两个节点已经连在一起了,再加入这条边一定就出现环了。
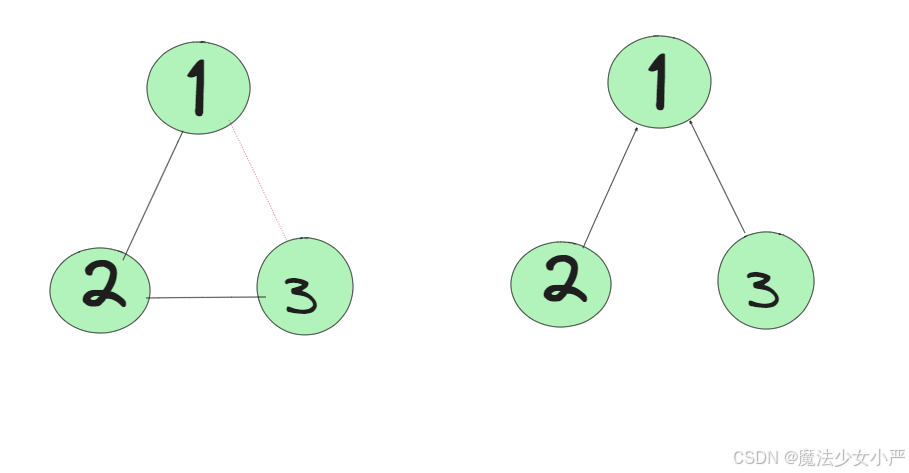
已经判断 节点1和 节点3 在在同一个集合(同一个根),如果将 节点1 和 节点3连在一起就一定会出现环。
import java.util.*; public class Main { public static void main(String[] args) { int n; Scanner in = new Scanner(System.in); n = in.nextInt(); M m = new M(n); while (in.hasNextLine()) { int x = in.nextInt(); int y = in.nextInt(); if (m.isSame(x, y)) { System.out.println(x + " " + y); return; } m.join(x, y); } } } class M { int[] father; public M(int n) { father = new int[n + 1]; for (int i = 1; i <= n; i++) { father[i] = i; } } int find(int i) { if (father[i] == i) { return i; } father[i] = find(father[i]); return father[i]; } boolean isSame(int i, int j) { i = find(i); j = find(j); if (i == j) return true; return false; } void join(int i, int j) { i = find(i); j = find(j); if (i == j) return; father[j] = i; } }109. 冗余连接II
时间限制:1.000S 空间限制:256MB
题目描述
有向树指满足以下条件的有向图。该树只有一个根节点,所有其他节点都是该根节点的后继。该树除了根节点之外的每一个节点都有且只有一个父节点,而根节点没有父节点。有根树拥有 n 个节点和 n - 1 条边。
输入一个有向图,该图由一个有着 n 个节点(节点编号 从 1 到 n),n 条边,请返回一条可以删除的边,使得删除该条边之后该有向图可以被当作一颗有向树。
输入描述
第一行输入一个整数 N,表示有向图中节点和边的个数。
后续 N 行,每行输入两个整数 s 和 t,代表 s 节点有一条连接 t 节点的单向边
输出描述
输出一条可以删除的边,若有多条边可以删除,请输出标准输入中最后出现的一条边。
输入示例
3 1 2 1 3 2 3输出示例
2 3提示信息
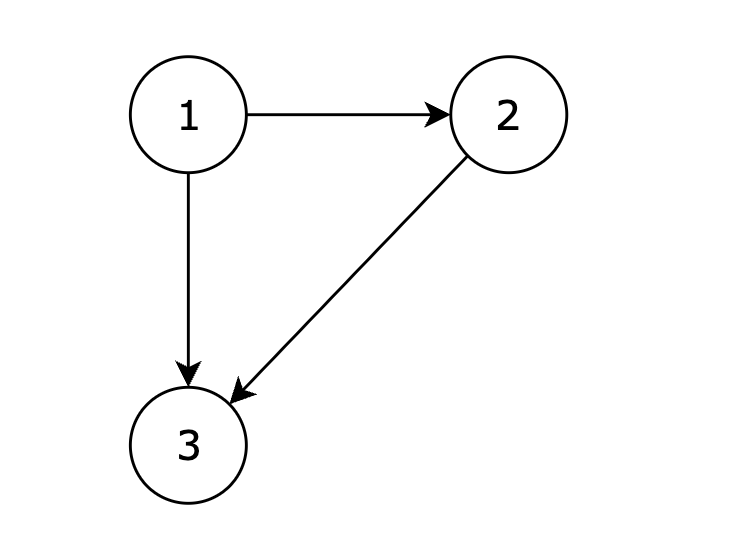
在删除 2 3 后有向图可以变为一棵合法的有向树,所以输出 2 3
数据范围:
1 <= N <= 1000.
思路:
本题的本质是 :有一个有向图,是由一颗有向树 + 一条有向边组成的 (所以此时这个图就不能称之为有向树),现在让我们找到那条边 把这条边删了,让这个图恢复为有向树。
还有“若有多条边可以删除,请输出标准输入中最后出现的一条边”,这说明在两条边都可以删除的情况下,要删顺序靠后的边!
向树的性质,如果是有向树的话,只有根节点入度为0,其他节点入度都为1(因为该树除了根节点之外的每一个节点都有且只有一个父节点,而根节点没有父节点)。
如果发现入度为2的节点,我们需要判断 删除哪一条边(导致入度为2的边),删除后本图能成为有向树。如果是删哪个都可以,优先删顺序靠后的边。
删除特定的边才能变成有向树
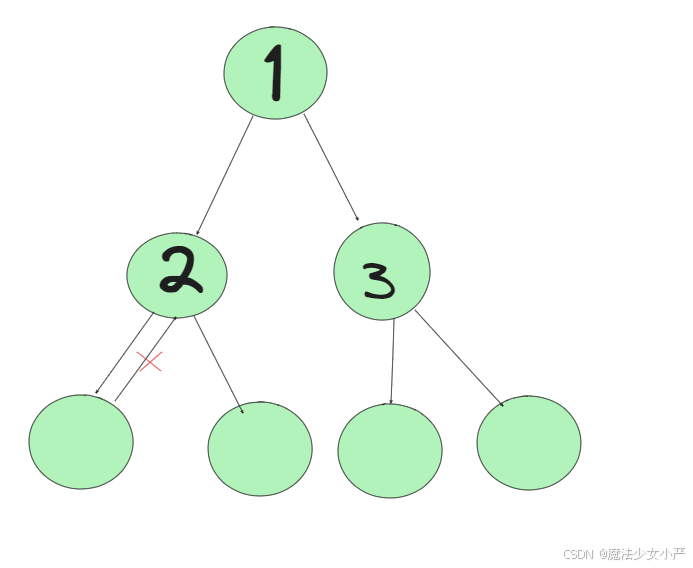
删除多条都可以,则删除最后加入的那条
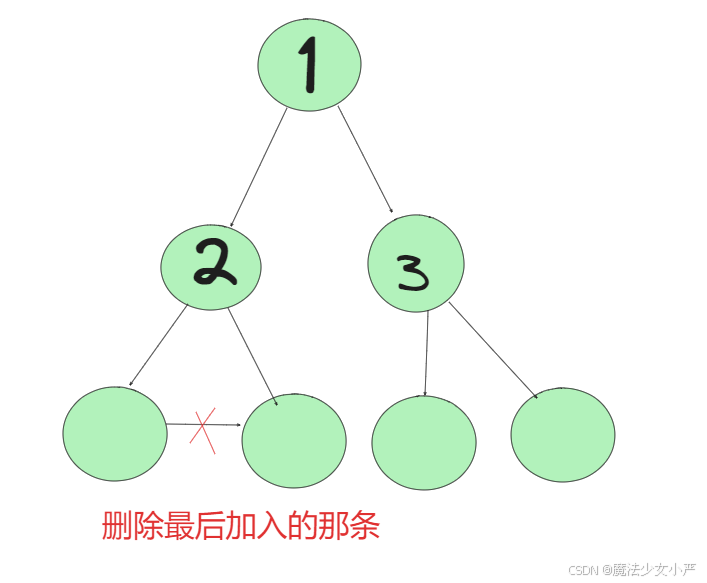
如果没有入度为2的点,说明 图中有环了(注意是有向环)。对于情况二,删掉构成环的边就可以了。
isTreeAfterRemoveEdge()判断删一个边之后是不是有向树(没有环且没有): 将所有边的两端节点分别加入并查集,遇到要 要删除的边则跳过,如果遇到即将加入并查集的边的两端节点 本来就在并查集了,说明构成了环。
如果顺利将所有边的两端节点(除了要删除的边)加入了并查集,则说明 删除该条边 还是一个有向树
getRemoveEdge()确定图中一定有了有向环,那么要找到需要删除的那条边: 将所有边的两端节点分别加入并查集,如果遇到即将加入并查集的边的两端节点 本来就在并查集了,说明构成了环。
代码参考:
import java.util.*; public class Main { private static M m; public static void main(String[] args) { int n; Scanner in = new Scanner(System.in); n = in.nextInt(); m = new M(n); int[] inDegree = new int[n + 1]; List<List<Integer>> edges = new LinkedList<>(); while (n-->0) { int x = in.nextInt(); int y = in.nextInt(); //记录下每个点的入度 inDegree[y]++; List<Integer> list = Arrays.asList(x, y); edges.add(list); } List<Integer> inedges2 = new LinkedList<>(); //找到入度为2的边 for (int i = edges.size() - 1; i >= 0; i--) { if (inDegree[edges.get(i).get(1)] == 2) { inedges2.add(i); } } if (inedges2.size() >0) { if (isTreeAfterRemoveEdge(inedges2.get(0), edges)) { System.out.println(edges.get(inedges2.get(0)).get(0) + " " + edges.get(inedges2.get(0)).get(1)); } else { System.out.println(edges.get(inedges2.get(1)).get(0) + " " + edges.get(inedges2.get(1)).get(1)); } } else { getRemoveEdge(edges); } } public static void getRemoveEdge(List<List<Integer>> edges) { m.init(); //遍历所有边,加入并查集 for (List<Integer> list : edges) { if (m.isSame(list.get(0), list.get(1))) { System.out.println(list.get(0) + " " + list.get(1)); return; } else { m.join(list.get(0), list.get(1)); } } } //判断删除该边后是否为有向树 public static boolean isTreeAfterRemoveEdge(int index, List<List<Integer>> edges) { m.init(); for(int i=0;i<edges.size();i++){ if(i!=index){ if (m.isSame(edges.get(i).get(0),edges.get(i).get(1))){ return false; } m.join(edges.get(i).get(0),edges.get(i).get(1)); } } return true; } } class M { int[] father; public M(int n) { father = new int[n + 1]; } void init() { for (int i = 1; i < father.length; i++) { father[i] = i; } } int find(int i) { if (father[i] == i) { return i; } father[i] = find(father[i]); return father[i]; } boolean isSame(int i, int j) { i = find(i); j = find(j); if (i == j) return true; return false; } void join(int i, int j) { i = find(i); j = find(j); if (i == j) return; father[j] = i; } }