目录
题目一:N 叉树的层序遍历
给定一个 N 叉树,返回其节点值的层序遍历。(即从左到右,逐层遍历)。
树的序列化输入是用层序遍历,每组子节点都由 null 值分隔(参见示例)。
示例 1:
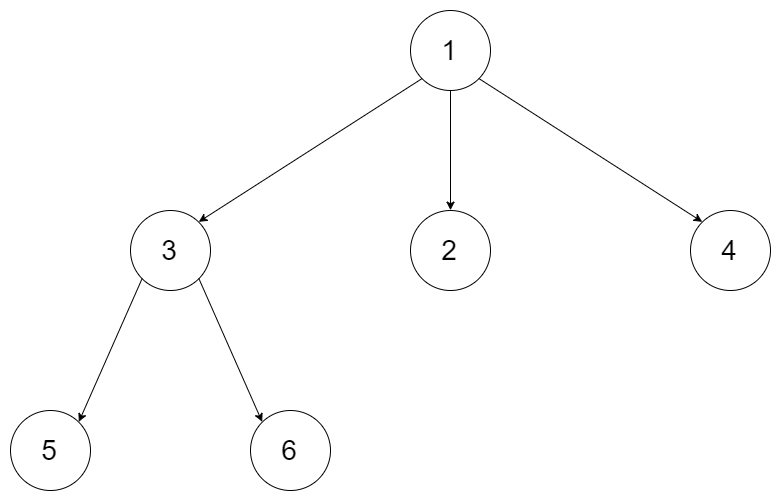
输入:root = [1,null,3,2,4,null,5,6] 输出:[[1],[3,2,4],[5,6]]
示例 2:
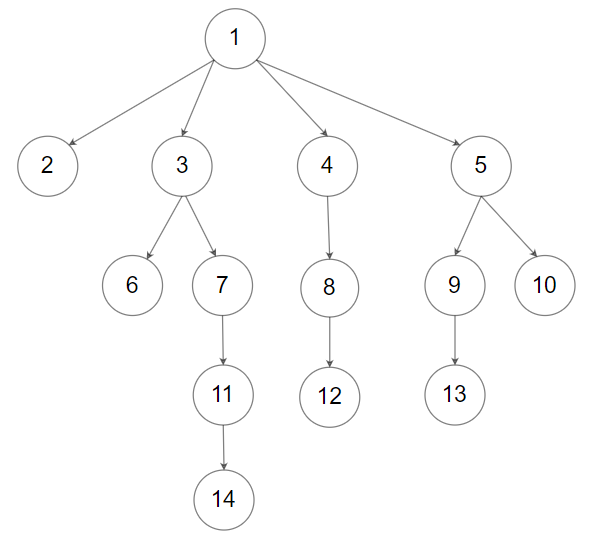
输入:root = [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14] 输出:[[1],[2,3,4,5],[6,7,8,9,10],[11,12,13],[14]]
提示:
- 树的高度不会超过
1000 - 树的节点总数在
[0, 104]之间
队列就是服务于宽搜这样的算法
在二叉树部分,我们有做过二叉树的层序遍历,这里是多叉树的层序遍历,其实方法还是一样的
每次将root结点入队列, 此时判断队列中有几个元素,有几个元素就说明这一层有几个结点,所以就出队列几次,每次出完这一次层数后就push_back进一个vector中
代码如下:
class Solution { public: vector<vector<int>> levelOrder(Node* root) { queue<Node*> q; // 层序遍历需要的队列 vector<vector<int>> vv; //记录最终结果 if(root == nullptr) return vv; q.push(root); while(!q.empty()) { int count = q.size(); // 求出本层元素的个数 vector<int> tmp; // 统计本层的节点 while(count--) { Node* cur = q.front(); q.pop(); tmp.push_back(cur->val); if(!cur->children.empty()) { // 让下一层节点入队 for(auto it : cur->children) q.push(it); } } vv.push_back(tmp); } return vv; } };题目二:二叉树的锯齿形层序遍历
给你二叉树的根节点 root ,返回其节点值的 锯齿形层序遍历 。(即先从左往右,再从右往左进行下一层遍历,以此类推,层与层之间交替进行)。
示例 1:
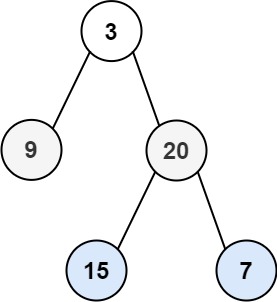
输入:root = [3,9,20,null,null,15,7] 输出:[[3],[20,9],[15,7]]
示例 2:
输入:root = [1] 输出:[[1]]
示例 3:
输入:root = [] 输出:[]
提示:
- 树中节点数目在范围
[0, 2000]内 -100 <= Node.val <= 100
这道题依旧是层序遍历的变形,每一层换个方向,可以发现,只是在偶数行的节点逆序即可,所以与上一题一样,只需要在偶数行存储进 vector<vector<int>> 时逆序
只需要加一个变量,可以是bool类型,每一次取相反的结果,假设第一层变量置为 false,那就每次偶数行的时候变量为 true,此时将插入的结果逆序即可
也可以是 int 类型,变量是几就表示第几层,层数 % 2 等于 0 就逆序
下面我采用设定 bool 类型的方式,代码如下:
class Solution { public: vector<vector<int>> zigzagLevelOrder(TreeNode* root) { vector<vector<int>> ret; queue<TreeNode*> q; // 如果为空,直接返回 if(root == nullptr) return ret; // 创建一个变量flag,当false的时候就将结果逆序 bool flag = false; q.push(root); while(!q.empty()) { // 计算每层的结点个数 int count = q.size(); vector<int> tmp; while(count--) { TreeNode* front = q.front(); q.pop(); tmp.push_back(front->val); // 判断左右孩子是否存在 if(front->left) q.push(front->left); if(front->right) q.push(front->right); } // 如果flag是true就逆序 if(flag) reverse(tmp.begin(), tmp.end()); ret.push_back(tmp); // 每次flag取反 flag = !flag; } return ret; } };题目三:二叉树最大宽度
给你一棵二叉树的根节点 root ,返回树的 最大宽度 。
树的 最大宽度 是所有层中最大的 宽度 。
每一层的 宽度 被定义为该层最左和最右的非空节点(即,两个端点)之间的长度。将这个二叉树视作与满二叉树结构相同,两端点间会出现一些延伸到这一层的 null 节点,这些 null 节点也计入长度。
题目数据保证答案将会在 32 位 带符号整数范围内。
示例 1:
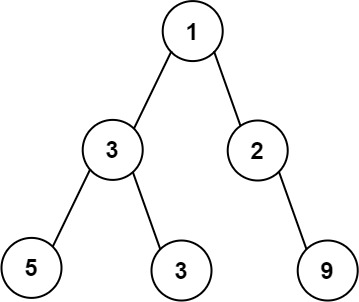
输入:root = [1,3,2,5,3,null,9] 输出:4 解释:最大宽度出现在树的第 3 层,宽度为 4 (5,3,null,9) 。
示例 2:
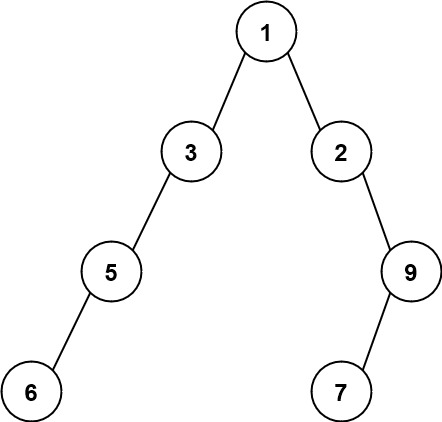
输入:root = [1,3,2,5,null,null,9,6,null,7] 输出:7 解释:最大宽度出现在树的第 4 层,宽度为 7 (6,null,null,null,null,null,7) 。
示例 3:
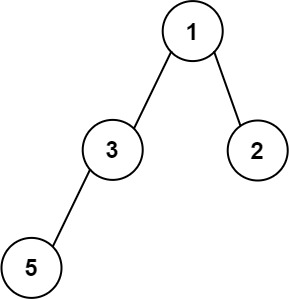
输入:root = [1,3,2,5] 输出:2 解释:最大宽度出现在树的第 2 层,宽度为 2 (3,2) 。
提示:
- 树中节点的数目范围是
[1, 3000] -100 <= Node.val <= 100
这个二叉树的最大宽度,其中的条件需要注意,只看第一个和最后一个结点,他们之间的结点如果是 nullptr 也是需要计算进去的
也就是说,统计宽度的时候是需要将二叉树当做满二叉树来统计的
这时就想到,二叉树可以存储在数组中,所以每一个结点就有对应的下标,通过下标就可以算出它的左右孩子的下标,此时每一层的最大宽度 = 最后一个结点的下标 - 第一个结点的下标 + 1
还有两个细节:
细节一:这里的队列可以用数组代替,因为数组取下标更方便
细节二:有可能发生下标溢出的问题,因为题目有可能所给出的二叉树每一层只有一个结点,此时层数非常高,但是这里的溢出并不影响结果的正确性,因为我们要的只是一个长度,而内存中存储是按照环形存储的,题目又告诉答案一定在32位整数范围内
所以即使溢出了,两个小标之差也是正确的结果,由于这里可能出现溢出,所以存储时就使用无符号整数来存储,此时就不会出现溢出的错误了
代码如下:
class Solution { public: int widthOfBinaryTree(TreeNode* root) { vector<pair<TreeNode*, unsigned int>> q; q.push_back({root, 1}); unsigned int ret = 0; while(!q.empty()) { // pair类型就可以使用下面这种方式,x1表示first,x2表示second auto& [x1, y1] = q[0]; auto& [x2, y2] = q[q.size() - 1]; ret = max(ret, y2 - y1 + 1); // 因为需要头删,vector头删效率低,所以重新创建一个vector存下一层的结点 vector<pair<TreeNode*, unsigned int>> tmp; for(auto& [x, y] : q) { if(x->left) tmp.push_back({x->left, 2 * y}); if(x->right) tmp.push_back({x->right, 2 * y + 1}); } // 将该层的结点全部存入tmp后,赋值给q,避免了头删 q = tmp; } return ret; } };题目四:在每个树行中找最大值
给定一棵二叉树的根节点 root ,请找出该二叉树中每一层的最大值。
示例1:
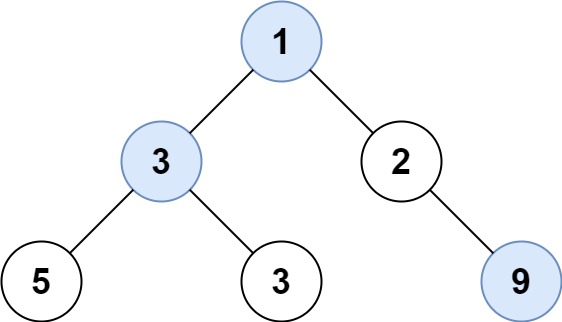
输入: root = [1,3,2,5,3,null,9] 输出: [1,3,9]
示例2:
输入: root = [1,2,3] 输出: [1,3]
提示:
- 二叉树的节点个数的范围是
[0,104] -231 <= Node.val <= 231 - 1
这道题题意非常简单,将每一层的最大值放入vector中
只需层序遍历时,找出每一层的最大值,存入即可
代码如下:
class Solution { public: vector<int> largestValues(TreeNode* root) { vector<int> ret; // 如果是空树,直接return if(root == nullptr) return ret; queue<TreeNode*> q; q.push(root); // 层序遍历 while(!q.empty()) { // num表示每层的最大值,初始化为int的最小值 int num = INT_MIN; int count = q.size(); while(count--) { TreeNode* front = q.front(); q.pop(); // num更新成最大值 num = max(num, front->val); if(front->left) q.push(front->left); if(front->right) q.push(front->right); } // 将最大值存入ret ret.push_back(num); } return ret; } };本节题目到此结束了
