最小角回归算法简介
最小角回归(Least Angle Regression, LAR)是一种用于回归分析的统计方法,它在某些方面类似于最小二乘回归,但提供了一些额外的优点。最小角回归由Bradley Efron等人提出,主要用于处理具有高度相关性的特征集。
最小角回归算法的核心思想是逐步添加特征到模型中,每次添加与当前残差相关性最大的特征。这个过程通过最小化角(即特征与残差之间的夹角)来实现,从而确保模型的稀疏性。这使得LAR算法在处理具有多重共线性的数据集时特别有用。
我们直接看最基本的LAR算法,假设有N个样本,自变量是p维的:
- 先对
 做标准化处理,使得每个predictor(
做标准化处理,使得每个predictor( 的每列)满足
的每列)满足 ,
, 。我们先假设回归模型中只有截距项,则
。我们先假设回归模型中只有截距项,则 ,记残差
,记残差 ,而其他的系数
,而其他的系数 。
。 - 找出与
 相关性最大的
相关性最大的 ,加入active set;
,加入active set; - 将
 从0逐步向LS系数
从0逐步向LS系数 变动,直到有另一个
变动,直到有另一个 ,它与
,它与 的相关系数绝对值,和
的相关系数绝对值,和 与
与 的相关系数绝对值一样大;
的相关系数绝对值一样大; - 将
 和
和 同时向二者的联合LS系数变动,直到再出现下一个
同时向二者的联合LS系数变动,直到再出现下一个 ,它与
,它与 的相关系数满足上一步的条件;
的相关系数满足上一步的条件; - 重复上述过程,
 步后,就得到完整的LS解。
步后,就得到完整的LS解。
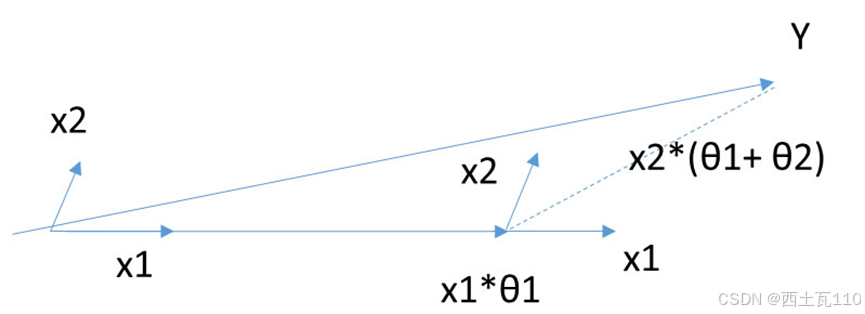
最小角回归算法主要解决的问题
- 多重共线性:数据集中的特征之间存在高度相关性,这可能导致最小二乘回归模型的参数估计不稳定。
- 特征选择:在特征数量多于样本数量的情况下,需要选择对模型预测最有帮助的特征子集。
- 稀疏模型:需要一个具有较少非零系数的模型,以便于解释和减少模型复杂度。
- 稳健性:在数据中存在噪声或异常值时,需要一个对这些情况不敏感的模型。
- 预测准确性:在保持模型简洁的同时,追求较高的预测准确性。
- 线性回归问题:LAR可以应用于标准的线性回归问题,即预测一个连续的响应变量。
- 逻辑回归问题:通过适当的修改,LAR也可以应用于分类问题,如逻辑回归。
- 多元回归问题:LAR可以处理多个响应变量的回归问题,即多元线性回归。
- 正则化问题:LAR提供了一种正则化方法,可以控制模型的复杂度,防止过拟合。
- 交叉验证问题:在模型选择过程中,LAR可以用于交叉验证,以选择最佳的模型复杂度。
- 模型解释性:由于LAR倾向于产生稀疏模型,因此它可以提高模型的可解释性。
- 大规模数据集:LAR算法适用于大规模数据集,尤其是当数据集中的特征数量非常多时。
最小角回归算法基本思想和理论基础
最小角回归算法基本思想
- 稀疏模型:LAR的目标是构建一个稀疏的回归模型,即模型中只有少数几个特征具有非零系数,这有助于提高模型的可解释性和降低过拟合的风险。
- 逐步添加特征:LAR通过逐步添加特征到模型中来构建。在每一步中,算法选择当前与残差相关性最大的特征加入模型,这个过程是迭代的。
- 最小化角:LAR的核心思想是最小化特征向量与残差向量之间的夹角。这个夹角的大小代表了特征对当前残差解释能力的大小。选择夹角最小的特征意味着选择了最能解释当前残差的特征。
- 正则化:LAR通过正则化项控制模型的复杂度,类似于LASSO算法,但LAR的正则化是通过最小化角来实现的,而不是直接对系数的大小进行惩罚。
- 数据驱动:LAR算法是数据驱动的,它根据数据本身的特性来选择特征,而不是依赖于预先设定的模型假设。
- 稳健性:由于LAR算法在每一步都考虑了特征与残差的相关性,它对数据中的噪声和异常值具有一定的稳健性。
- 快速计算:LAR算法利用了数据的稀疏性质和快速的更新规则,使得算法在计算上相对高效。
- 灵活性:LAR算法可以应用于不同类型的回归问题,包括线性回归、逻辑回归等,并且可以处理大规模数据集。
- 交叉验证:LAR算法可以结合交叉验证等方法来选择最佳的正则化参数,实现模型的自动选择。
- 模型解释性:由于LAR倾向于产生稀疏模型,它提高了模型的可解释性,使得模型更容易被理解和应用。
最小角回归算法理论基础
- 线性回归问题:LAR算法是针对线性回归问题设计的,它通过逐步添加特征的方式进行特征选择和回归系数的计算 。
- 特征向量分解:LAR算法的核心在于将回归目标向量分解为若干组特征向量的线性组合,关键在于选择正确的特征向量分解顺序和分解系数 。
- 前向选择算法:LAR算法与前向选择算法(Forward Selection)有关,前向选择算法是一种贪婪算法,通过选择与目标向量相关度最高的特征向量进行分解 。
- 前向梯度算法:LAR算法也与前向梯度算法(Forward Stagewise)有关,该算法通过小步试错的方式进行特征向量的选择和分解 。
- 最小化角:LAR算法通过最小化特征向量与残差向量之间的夹角来进行特征选择,这种方法结合了前向选择算法的快速性和前向梯度算法的准确性 。
- 正则化方法:LAR算法是一种正则化方法,它可以求解Lasso回归问题,并且可以得到Lasso解的路径 。
- 算法性质:LAR算法保持最小角的性质,即在分解过程中,每个predictor与残差向量的相关系数会同比例地减少 。
- 模型的求解:LAR算法通过逐步更新残差向量和逐步调整回归系数,直到满足终止条件,如残差向量足够小或所有变量都已使用完毕 。
- 稳定性和灵活性:LAR算法具有很好的稳定性和灵活性,适用于特征维度远高于样本数的情况,并且可以容易地修改以适应其他估算器,如LASSO 。
- 算法效率:LAR算法在计算上非常有效,特别是当特征维度远大于样本数量时,它的计算速度几乎和前向选择算法一样快
最小角回归算法步骤
1.初始化:
将所有特征的系数初始化为零。
计算初始残差向量,即响应向量与所有特征系数为零时的残差。
2.标准化特征:
为了确保算法不受特征尺度的影响,对所有特征向量进行标准化处理。
3.构建活动集:
初始化一个活动集(active set),包含与当前残差向量相关性最大的特征。
4.计算相关性:
对于每个特征,计算它与当前残差向量的相关系数。
5.选择特征:
选择与当前残差向量相关性最大的特征,将其添加到活动集中。
6.更新系数:
对活动集中的每个特征,逐步更新其系数,直到另一个特征的相关性与当前特征相同。
7.调整系数:
当两个或多个特征与残差向量的相关性相等时,同时更新这些特征的系数,直到它们的相关性不再相等。
8.更新残差:
使用当前的系数和特征向量来更新残差向量。
9.检查终止条件:
如果残差向量的范数低于某个阈值,或者已经没有更多的特征可以添加到模型中,则算法终止。
10.重复迭代:
重复步骤4到9,直到满足终止条件。
11.输出结果:
最终,算法输出模型的系数向量,这些系数代表了特征对响应变量的影响。
最小角回归算法推导
保持最小角
我们先来看LS估计量的一个性质:若每个predictor与 的相关系的数绝对值相等,从此时开始,将所有系数的估计值同步地从0移向LS估计量,在这个过程中,每个predictor与残差向量的相关系数会同比例地减少。
的相关系的数绝对值相等,从此时开始,将所有系数的估计值同步地从0移向LS估计量,在这个过程中,每个predictor与残差向量的相关系数会同比例地减少。
假设我们标准化了每个predictor和 ,使他们均值为0,标准差为1。在这里的设定中,对于任意
,使他们均值为0,标准差为1。在这里的设定中,对于任意 ,都有
,都有 ,其中
,其中 为常数。LS估计量
为常数。LS估计量 ,当我们将系数从0向
,当我们将系数从0向 移动了
移动了![\alpha(\alpha\in[0,1])](/zb_users/upload/2024/csdn/eq.png) 比例时,记拟合值为
比例时,记拟合值为 。
。
另外,记 为只有第
为只有第 个元素为1、其他元素均为0的
个元素为1、其他元素均为0的 维向量,则
维向量,则 ,再记,记投影矩阵
,再记,记投影矩阵 。
。
这里的问题是,在 变大过程中,每一个
变大过程中,每一个 与新的残差的相关系数,是否始终保持相等?且是否会减小?
与新的残差的相关系数,是否始终保持相等?且是否会减小?
由于![\left| x_{\cdot j}' [y-u(\alpha)]\right|=\left|x_{\cdot j}'y - \ell_p^{(j)\prime} X' u(\alpha)\right|=(1-\alpha)N\lambda](/zb_users/upload/2024/csdn/eq.png) ,即内积与
,即内积与 无关。再由
无关。再由 可知
可知 。
。
相关系数的绝对值
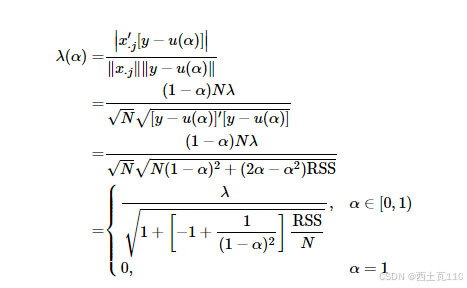
因此,任意predictor与当前残差的相关系数绝对值,会随着 的增加,同比例地减小,并且
的增加,同比例地减小,并且 。
。
现在,我们再回顾一下LAR的过程。在第 步开始时,将所有active set中的predictor的集合记为
步开始时,将所有active set中的predictor的集合记为 ,此时在上一步估计完成的系数为
,此时在上一步估计完成的系数为 ,它是维且每个维度都非零的向量,记此时残差为
,它是维且每个维度都非零的向量,记此时残差为 ,用
,用 对
对 做回归后系数为
做回归后系数为 ,拟合值
,拟合值 。另外,我们知道
。另外,我们知道 ,而一个predictor加入
,而一个predictor加入 的条件就是它与当前
的条件就是它与当前 的相关系数的绝对值等于
的相关系数的绝对值等于 中的predictor与当前
中的predictor与当前 的相关系数的绝对值,所以
的相关系数的绝对值,所以 向量的每个维度的绝对值都相等,也即
向量的每个维度的绝对值都相等,也即 ′的每个维度的绝对值都相等,
′的每个维度的绝对值都相等, 就是与各个
就是与各个 中的predictor的角度都相等的向量,且与它们的角度是最小的,而
中的predictor的角度都相等的向量,且与它们的角度是最小的,而 也是下一步系数要更新的方向,这也是“最小角回归”名称的由来。
也是下一步系数要更新的方向,这也是“最小角回归”名称的由来。
参数更新
那么,在这个过程中,是否需要每次都逐步小幅增加 ,再检查有没有其他predictor与残差的相关系数绝对值?有没有快速的计算的方法?答案是有的。
,再检查有没有其他predictor与残差的相关系数绝对值?有没有快速的计算的方法?答案是有的。
在第 步的开始,
步的开始, 中有
中有 个元素,我们记
个元素,我们记 ,其中
,其中 ,并记
,并记 ,此时的active set其实就是
,此时的active set其实就是 。在这里,我们将
。在这里,我们将 做个修改,记
做个修改,记 ,再令
,再令![X_{\mathcal{A}_k}=[\cdots s_jx_{\cdot j}\cdots]_{j\in\mathcal{A}_k}](/zb_users/upload/2024/csdn/eq.png) 。
。
此时更新方向为 ,并取
,并取 。更新的规则为
。更新的规则为 。因此,任一predictor,与当前残差的内积就为
。因此,任一predictor,与当前残差的内积就为 ,而对于
,而对于 ,有
,有 。
。
对于 ,如果要使与当前残差的相关系数绝对值,与在
,如果要使与当前残差的相关系数绝对值,与在 中的predictor与当前残差的相关系数绝对值相等,也即它们的内积的绝对值相等,必须要满足
中的predictor与当前残差的相关系数绝对值相等,也即它们的内积的绝对值相等,必须要满足 。问题转化为了求解使它们相等的
。问题转化为了求解使它们相等的 ,并对于所有的
,并对于所有的 ,最小
,最小 的即为最后的更新步长。
的即为最后的更新步长。
由于 ,因此只需考虑
,因此只需考虑 与
与 的大小关系即可。最后解为
的大小关系即可。最后解为

注意到
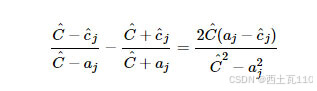
因此,当 时,除非
时,除非 即
即 ,否则必有
,否则必有 。反之,当
。反之,当 时,除非
时,除非 即
即 ,否则必有
,否则必有 。综上所述,上面的解可以写为
。综上所述,上面的解可以写为
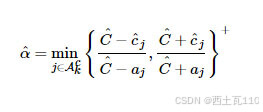
其中 表示只对其中正的元素有效,而丢弃负的元素。
表示只对其中正的元素有效,而丢弃负的元素。
最小角回归算法代码实现
import numpy as np from sklearn.preprocessing import StandardScaler from sklearn.linear_model import Lars import matplotlib.pyplot as plt # 示例数据生成 np.random.seed(0) X = 2.5 - 1.5 * np.random.randn(100, 1) y = 1 + 2 * X + 0.5 * np.random.randn(100, 1) # 添加截距项 X = np.hstack([np.ones((100, 1)), X]) # 数据标准化 scaler = StandardScaler() X_scaled = scaler.fit_transform(X) # 创建LARS模型实例 lars = Lars() # 拟合模型 lars.fit(X_scaled, y) # 打印系数 print("Coefficients:", lars.coef_) # 绘制系数路径 plt.plot(lars.coef_, drawstyle="steps") plt.xlabel("Variables") plt.ylabel("Coefficient Value") plt.title("Coefficient Path of LARS") plt.show()最小角回归算法具有以下优缺点
优点:
- 高维数据处理:LAR算法特别适合于特征维度 n 远高于样本数 m 的情况,能够有效处理高维数据 。
- 计算效率:算法的最坏计算复杂度与最小二乘法类似,但计算速度几乎与前向选择算法一样快 。
- 系数路径:LAR算法可以产生分段线性结果的完整路径,这在模型的交叉验证中非常有用 。
- 稳定性:如果两个变量对响应有几乎相等的联系,则LAR算法会给予它们相似的系数增长率,这与我们的直觉判断一致,且更加稳定 。
- 灵活性:LAR算法容易修改并为其他估算器生成解,例如可以用于求解Lasso回归问题 。
缺点:
- 对噪声敏感:由于LAR算法的迭代方向是根据目标残差而定,因此该算法对样本的噪声非常敏感 。
- 实现复杂性:尽管算法本身在理论上具有吸引力,但在实际实现时可能较为复杂,特别是对于非专家用户 。
最小角回归算法的应用场景
- 高维数据回归问题:LAR算法特别适用于处理特征数量多于样本数量的高维数据集,能够有效地进行变量选择和回归分析 。
- 生物信息学:在生物信息学领域,LAR可以用于处理基因表达数据,识别重要的生物标记 。
- 金融分析:LAR在量化分析和风险预测中应用,帮助分析金融数据和预测市场趋势 。
- 信号处理:在信号处理领域,LAR可以用于信号恢复和噪声减少,提高信号的质量 。
- 大规模数据分析:对于特征众多的数据集,LAR进行有效的变量选择和数据压缩,简化模型并提高解释能力 。
- 特征选择:LAR算法提供了一种高效的特征选择方式,尤其在变量个数远大于样本数的情况下,能够快速识别出重要的特征 。
- 稳健性分析:LAR算法在变量选择上表现出较高的稳定性,对于高度相关的变量,提供了更加稳健的解决方案 。
- 教育和研究:在教育和研究领域,LAR算法被用于教学和研究项目,帮助学生和研究人员理解高维数据的回归分析方法 。
模型优化:通过使用网格搜索(GridSearchCV)和交叉验证的方法来精细调整LAR模型的参数,期望获得最佳的模型性能 。
