贝叶斯岭回归算法简介
贝叶斯岭回归(Bayesian Ridge Regression)是一种回归分析方法,它结合了岭回归(Ridge Regression)的正则化特性和贝叶斯统计的推断能力。这种方法在处理具有大量特征的数据集时特别有用,因为它可以帮助减少模型的复杂性并防止过拟合。
线性回归是一种通过拟合输入特征与目标变量之间的线性关系来预测目标变量的统计方法。然而,当数据存在噪声或多重共线性时,传统的最小二乘法可能会导致过拟合问题,即模型在训练数据上表现良好,但在新数据上泛化能力差。岭回归通过在目标函数中加入正则化项(通常是L2正则化)来约束回归系数的大小,从而减轻过拟合问题。但岭回归中的正则化参数需要手动选择,这增加了模型选择的难度。
贝叶斯岭回归则通过贝叶斯方法自动估计正则化参数,并提供了对回归系数不确定性的估计,从而解决了上述问题
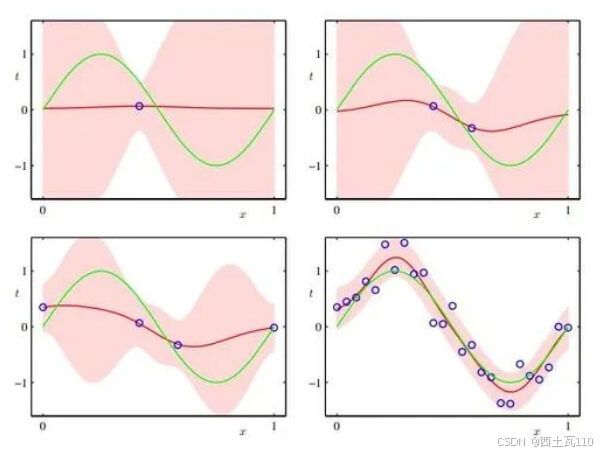
贝叶斯岭回归算法基本原理
- 岭回归的引入:在传统的线性回归模型中,如果存在多重共线性(即特征之间高度相关),模型的参数估计可能会变得不稳定。岭回归通过在损失函数中添加一个正则化项(通常是参数的平方和)来解决这个问题,这有助于收缩参数估计值,从而提高模型的稳定性。
- 贝叶斯框架:贝叶斯岭回归在岭回归的基础上,进一步采用贝叶斯统计的方法来估计模型参数。这意味着它使用先验分布来表达对参数的先验知识,并结合数据的似然性来更新这些知识,得到后验分布。
- 先验和后验:贝叶斯岭回归为每个回归系数赋予一个高斯先验,并且每个先验的方差由一个超参数控制,这个超参数本身也可以通过贝叶斯推断来估计。通过这种方式,模型可以自动调整正则化强度,而不需要手动选择。
贝叶斯岭回归算法的公式
贝叶斯岭回归(Bayesian Ridge Regression)的公式涉及多个组成部分,主要是贝叶斯统计中的先验分布、似然函数以及后验分布的推导。以下是对贝叶斯岭回归中关键公式的简要概述:
先验分布
在贝叶斯岭回归中,我们假设回归系数 w 的先验分布是一个以零为中心的高斯分布(也称为正态分布),其协方差矩阵与正则化参数 λ 有关:

其中,I 是单位矩阵,λ 是正则化参数(也称为精度参数),它控制了先验分布中 w 的分散程度。
似然函数
给定观测数据 X 和 y,我们假设观测噪声 ϵ 是高斯噪声,因此似然函数也是高斯分布:
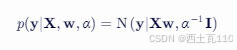
其中,α 是噪声精度参数(与噪声方差 σ2 成反比,即 α=1/σ2),X 是设计矩阵(特征矩阵),y 是目标变量向量。
后验分布
根据贝叶斯定理,后验分布 p(w∣y,X,α,λ) 是先验分布和似然函数的乘积归一化后的结果。然而,直接计算后验分布可能很复杂,因此通常使用近似方法(如最大后验估计MAP)或采样方法(如马尔可夫链蒙特卡洛MCMC)。
在贝叶斯岭回归的上下文中,我们经常关注的是后验分布的均值和协方差,这些可以通过解析方式(在特定假设下)或数值方法(如变分推断)来近似。
预测分布
对于新的输入 x∗,我们想要预测其对应的输出 y∗。预测分布 p(y∗∣x∗,y,X,α,λ) 可以通过对 w 的后验分布进行积分来得到:
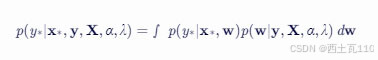
在实践中,我们通常对预测分布的均值和方差感兴趣,这些可以通过后验分布的均值和协方差来近似计算。
贝叶斯岭回归算法步骤
- 定义先验分布:选择合适的先验分布形式及其参数(如高斯分布的均值和协方差矩阵)。
- 计算似然函数:根据观测数据计算似然函数。
- 推导后验分布:利用贝叶斯定理和先验分布、似然函数推导出后验分布。由于后验分布可能比较复杂,通常需要使用近似方法(如最大后验估计MAP)或采样方法(如马尔可夫链蒙特卡洛MCMC)来估计其参数。
- 参数估计:通过优化算法(如梯度下降、共轭梯度法等)估计正则化参数 λ 和噪声精度参数 α(或等价地,噪声方差 σ2)。这些参数的选择对模型性能有重要影响。
- 预测:对于新的输入 x∗,利用后验分布进行预测。预测分布 p(y∗∣x∗,y,X,α,λ) 可以通过对 w 的后验分布进行积分来得到。
贝叶斯岭回归算法的代码实现
import numpy as np from sklearn.model_selection import train_test_split from sklearn.linear_model import BayesianRidge from sklearn.metrics import mean_squared_error # 示例数据 # 假设X是特征矩阵,y是目标变量 np.random.seed(0) n_samples, n_features = 100, 1 X = np.random.randn(n_samples, n_features) # 创建一个简单的线性关系:y = 3 * X + 2,并添加一些噪声 w = 3.0 c = 2.0 noise = np.random.randn(n_samples) y = w * X.ravel() + c + noise # 划分训练集和测试集 X_train, X_test, y_train, y_test = train_test_split(X,y,test_size=0.2,random_state=42) # 创建贝叶斯岭回归模型 model = BayesianRidge(tol=1e-6, fit_intercept=True, compute_score=True) # 训练模型 model.fit(X_train, y_train) # 预测测试集 y_pred = model.predict(X_test) # 评估模型 mse = mean_squared_error(y_test, y_pred) print(f"Mean Squared Error: {mse}") # 打印模型参数 print(f"Estimated weight: {model.coef_[0]}") print(f"Estimated intercept: {model.intercept_}") # 如果需要,还可以查看模型对权重的估计分布(尽管BayesianRidge不直接提供分布样本) # 但你可以通过查看模型的属性(如lambda_和alpha_)来了解正则化强度 print(f"Lambda (regularization strength): {model.lambda_}") print(f"Alpha (precision of the noise): {model.alpha_}")贝叶斯岭回归算法的优缺点
优点
- 自动正则化:贝叶斯岭回归模型能够自动地通过先验分布和数据来确定正则化参数的大小,避免了传统岭回归中需要手动调整正则化参数的繁琐过程。这使得模型更加灵活和自适应。
- 处理共线性问题:当数据中存在多重共线性问题时,贝叶斯岭回归模型能够通过引入先验分布来约束回归系数的大小,从而减轻共线性对模型性能的影响。
- 不确定性评估:贝叶斯岭回归模型不仅提供回归系数的点估计,还可以提供这些系数的后验分布。这为模型的不确定性评估提供了可能,有助于更好地理解模型的预测结果和潜在风险。
- 稳健性:由于贝叶斯岭回归模型考虑了参数的先验分布和观测数据的不确定性,因此它在处理噪声数据和异常值时表现出较高的稳健性。
缺点
- 计算复杂度较高:相比于传统的岭回归模型,贝叶斯岭回归模型的计算复杂度较高。这主要是因为需要计算后验分布和进行参数估计的迭代过程。因此,在数据量较大或模型复杂度较高时,可能需要较长的计算时间。
- 先验分布的选择:贝叶斯岭回归模型的性能受到先验分布选择的影响。如果先验分布与真实情况相差较大,可能会导致模型性能下降。因此,在实际应用中需要谨慎选择先验分布。
- 推断过程耗时:由于贝叶斯岭回归模型需要进行复杂的后验分布计算和参数估计迭代过程,因此其推断过程相对耗时。这可能会限制模型在某些实时性要求较高的场景中的应用。
贝叶斯岭回归算法的应用场景
贝叶斯岭回归模型(Bayesian Ridge Regression Model)作为一种结合了贝叶斯统计理论和岭回归的回归分析方法,具有自动正则化、处理共线性问题、不确定性评估和稳健性等优点。这些特点使得贝叶斯岭回归模型在多个领域具有广泛的应用场景。以下是一些典型的应用场景:
- 金融数据分析
在金融领域,贝叶斯岭回归模型可以用于股票价格预测、市场趋势分析、风险评估等。金融数据通常具有高维度、共线性和噪声多的特点,而贝叶斯岭回归模型能够自动处理这些问题,提供稳定的预测结果和风险评估。
- 生物信息学
在生物信息学领域,贝叶斯岭回归模型可以用于基因表达数据的分析、疾病预测和药物反应预测等。生物数据往往包含大量的基因和复杂的相互作用关系,贝叶斯岭回归模型能够通过考虑参数的先验分布和观测数据的不确定性,更好地捕捉这些复杂关系。
- 工业过程控制
在工业过程中,贝叶斯岭回归模型可以用于质量预测、故障诊断和过程优化等。工业过程通常包含多个变量和复杂的非线性关系,而贝叶斯岭回归模型能够通过正则化技术和贝叶斯推断来处理这些问题,提高预测准确性和系统稳定性。
- 医学诊断
在医学领域,贝叶斯岭回归模型可以用于疾病诊断、预后评估和个性化医疗等。医学数据通常包含患者的多种生理指标和临床信息,而贝叶斯岭回归模型能够考虑这些信息的先验分布和不确定性,提供更为准确的诊断结果和个性化治疗方案。
- 机器学习竞赛
在机器学习竞赛中,贝叶斯岭回归模型也是一种常用的工具。竞赛数据往往具有复杂性和多样性,而贝叶斯岭回归模型能够通过其自动正则化和不确定性评估的特点,提高模型的泛化能力和预测精度。
- 其他应用场景
除了以上几个典型应用场景外,贝叶斯岭回归模型还可以用于社会科学研究、市场营销分析、环境保护等多个领域。这些领域的数据分析往往也面临高维度、共线性、噪声多等挑战,而贝叶斯岭回归模型能够提供有效的解决方案。
