阅读量:0
House Prices - Advanced Regression Techniques | Kaggle
在这里下载数据,然后使用pandas读。
课本:4.10. 实战Kaggle比赛:预测房价 — 动手学深度学习 2.0.0 documentation (d2l.ai)
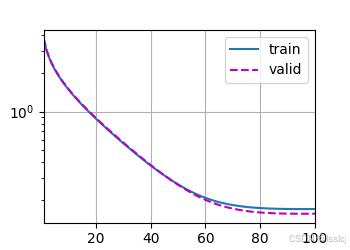
一层线性层
def get_net(): net = nn.Sequential(nn.Linear(in_features, 1)) # 输出房价 return net k, num_epochs, lr, weight_decay, batch_size = 5, 100, 5, 0, 64 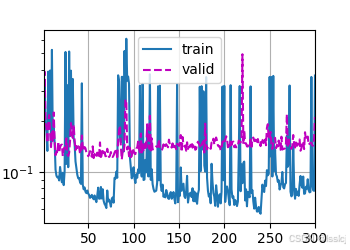
MLP
net = nn.Sequential(nn.Flatten(), nn.Linear(in_features, 128), nn.ReLU(), nn.Linear(128, 1)) k, num_epochs, lr, weight_decay, batch_size = 5, 300, 5, 6, 64 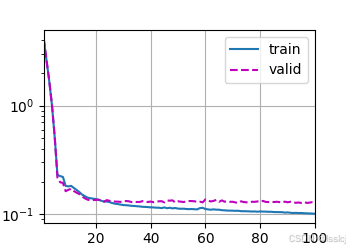
Xarvier初始化,MLP
def get_net(): #net = nn.Sequential(nn.Linear(in_features, 1)) # 输出房价 net = nn.Sequential(nn.Flatten(), nn.Linear(in_features, 128), nn.ReLU(), nn.Linear(128, 1)) return net def init_weights(m): if type(m) == nn.Linear: nn.init.xavier_normal_(m.weight) if m.bias is not None: nn.init.zeros_(m.bias) k, num_epochs, lr, weight_decay, batch_size = 5, 100, 0.1, 0.2, 128 完整代码
import numpy as np import pandas as pd import torch from torch import nn from d2l import torch as d2l train_data = pd.read_csv('D:/a-learn/summer_AI/kaggle/HousePrices/train.csv') test_data = pd.read_csv('D:/a-learn/summer_AI/kaggle/HousePrices/test.csv') print(train_data.shape) print(test_data.shape) print(train_data.iloc[0:4, [0, 1, 2, 3, -3, -2, -1]]) # 可以看到第一列特征是ID,对预测没有帮助,直接去掉 # train里面的最后一列是需要预测的值,这样train和test都是80行了 all_features = pd.concat((train_data.iloc[:, 1:-1], test_data.iloc[:, 1:])) '''数据预处理 将所有缺失的值替换为相应特征的平均值,通过将特征重新缩放到零均值和单位方差来标准化数据 下面先处理值为数字的特征,在处理值离散的特征 ''' numeric_features = all_features.dtypes[all_features.dtypes != 'object'].index # 如果dtype不是object,就是数值特征 all_features[numeric_features] = all_features[numeric_features].apply( lambda x: (x - x.mean()) / (x.std()) # 归一化 ) # 将方差变为1 all_features[numeric_features] = all_features[numeric_features].fillna(0) # 归一化后再将NaN填为0 # 处理离散值 # dummy_na意为值为NaN意为没有特征,pandas会帮我们处理NaN的值,注意get_dummies自动赋的是布尔值,需要自己使用dtype来调整 all_features = pd.get_dummies(all_features, dummy_na=True, dtype=int) # 至此已经全部处理好了,最后通过values属性,可以从pandas格式中提取NumPy格式,并将其转换为张量表示用于训练 n_train = train_data.shape[0] # 训练集数据的个数 # 将数据转换成为张量 train_features = torch.tensor(all_features[:n_train].values, dtype=torch.float32) test_features = torch.tensor(all_features[n_train:].values, dtype=torch.float32) # reshape(-1,1)将Numpy数组形状转换为一个二维数组,确保每个样本都有一个输出,即从形状(n,)转换为(n,1),n为样本数量 train_labels = torch.tensor(train_data.SalePrice.values.reshape(-1, 1), dtype=torch.float32) '''训练''' loss = nn.MSELoss() in_features = train_features.shape[1] # 输入的特征数 def get_net(): #net = nn.Sequential(nn.Linear(in_features, 1)) # 输出房价 net = nn.Sequential(nn.Flatten(), nn.Linear(in_features, 128), nn.ReLU(), nn.Linear(128, 1)) return net def init_weights(m): if type(m) == nn.Linear: nn.init.xavier_normal_(m.weight) if m.bias is not None: nn.init.zeros_(m.bias) # 对于房价,我们更关心相对误差(y-y')/y.可以使用对数来衡量差异 '''对数均方根误差''' def log_rmse(net, features, labels): clipped_preds = torch.clamp(net(features), 1, float('inf')) # 在取对数时,确保所有预测值至少为 1,以避免对数计算时出现负无穷或未定义的情况 rmse = torch.sqrt(loss(torch.log(clipped_preds), torch.log(labels))) return rmse.item() # 将张量转换为Python标量值 def train(net, train_features, train_labels, test_features, test_labels, num_epochs, learning_rate, weight_decay, batch_size): train_ls, test_ls = [], [] train_iter = d2l.load_array((train_features, train_labels), batch_size) # 这里使用的是Adam优化算法,对初始学习率不是很敏感 optimizer = torch.optim.Adam(net.parameters(), lr=learning_rate, weight_decay=weight_decay) for epoch in range(num_epochs): for X, y in train_iter: optimizer.zero_grad() # 梯度清0 l = loss(net(X), y) l.backward() optimizer.step() train_ls.append(log_rmse(net, train_features, train_labels)) if test_labels is not None: test_ls.append(log_rmse(net, test_features, test_labels)) return train_ls, test_ls # K折交叉验证 # 得到第i折的数据 def get_k_fold_data(k, i, X, y): # 分别是划分数,选取第几部分为验证集,输入,输出 assert k > 1 fold_size = X.shape[0] // k X_train, y_train = None, None for j in range(k): idx = slice(j * fold_size, (j + 1) * fold_size) X_part, y_part = X[idx, :], y[idx] if j == i: # 验证集 X_valid, y_valid = X_part, y_part elif X_train is None: X_train, y_train = X_part, y_part # 训练集为空则赋值 else: X_train = torch.cat([X_train, X_part], 0) # 不为空则连接,直接接在后面就行,dim=0 y_train = torch.cat([y_train, y_part], 0) return X_train, y_train, X_valid, y_valid def k_fold(k, X_train, y_train, num_epochs, learning_rate, weight_decay, batch_size): train_l_sum, valid_l_sum = 0, 0 for i in range(k): data = get_k_fold_data(k, i, X_train, y_train) net = get_net() net.apply(init_weights) # *data是对数据解码(取括号),得到get_k_fold_data返回的4个数据列表,依次传入train函数中 train_ls, valid_ls = train(net, *data, num_epochs, learning_rate, weight_decay, batch_size) train_l_sum += train_ls[-1] # 注意最后一列是对数均方根误差,没问题的 valid_l_sum += valid_ls[-1] if i == 0: d2l.plot(list(range(1, num_epochs + 1)), [train_ls, valid_ls], xlabel='epoch', ylabel='rmse', xlim=[1, num_epochs], legend=['train', 'valid'], yscale='log') print(f'折{i + 1},训练log rmse{float(train_ls[-1]):f}, ' f'验证log rmse{float(valid_ls[-1]):f}') return train_l_sum / k, valid_l_sum / k # k, num_epochs, lr, weight_decay, batch_size = 5, 100, 0.1, 0.2, 128 # train_l, valid_l = k_fold(k, train_features, train_labels, num_epochs, lr, # weight_decay, batch_size) # print(f'{k}-折验证: 平均训练log rmse: {float(train_l):f}, ' # f'平均验证log rmse: {float(valid_l):f}') # d2l.plt.show() #调好参数后,使用所有的数据作为训练,然后预测 def train_and_pred(train_features, test_features, train_labels, test_data, num_epochs, lr, weight_decay, batch_size): net = get_net() net.apply(init_weights) train_ls, _ = train(net, train_features, train_labels, None, None, num_epochs, lr, weight_decay, batch_size) d2l.plot(np.arange(1, num_epochs + 1), [train_ls], xlabel='epoch', ylabel='log rmse', xlim=[1, num_epochs], yscale='log') print(f'训练log rmse:{float(train_ls[-1]):f}') d2l.plt.show() # 将网络应用于测试集。 preds = net(test_features).detach().numpy() # 将其重新格式化以导出到Kaggle test_data['SalePrice'] = pd.Series(preds.reshape(1, -1)[0]) submission = pd.concat([test_data['Id'], test_data['SalePrice']], axis=1) submission.to_csv('submission.csv', index=False) train_and_pred(train_features, test_features, train_labels, test_data, 100, 0.1, 0.2, 128) 