将混沌映射方法与优化算法相结合是一种常见的改进方式。本期不完全整理了21种常见的混沌映射方法的matlab代码,并将他们运用在算法的初始化中。该策略适用于所有优化算法。具体有:
Chebyshev混沌映射 Circle 混沌映射 Gauss/mouse 混沌映射 Iterative 混沌映射 Logistic 混沌映射 Piecewise 混沌映射 Sine 混沌映射 Singer 混沌映射 Sinusoidal 混沌映射 Tent 混沌映射 Fuch 混沌映射 SPM 混沌映射 ICMIC 混沌映射 Tent-Logistic-Cosine 混沌映射 Sine-Tent-Cosine 混沌映射 Logistic-Sine-Cosine 混沌映射 Henon 混沌映射 Cubic 混沌映射 Logistic-Tent 混沌映射 Bernoulli 混沌映射 Kent 混沌映射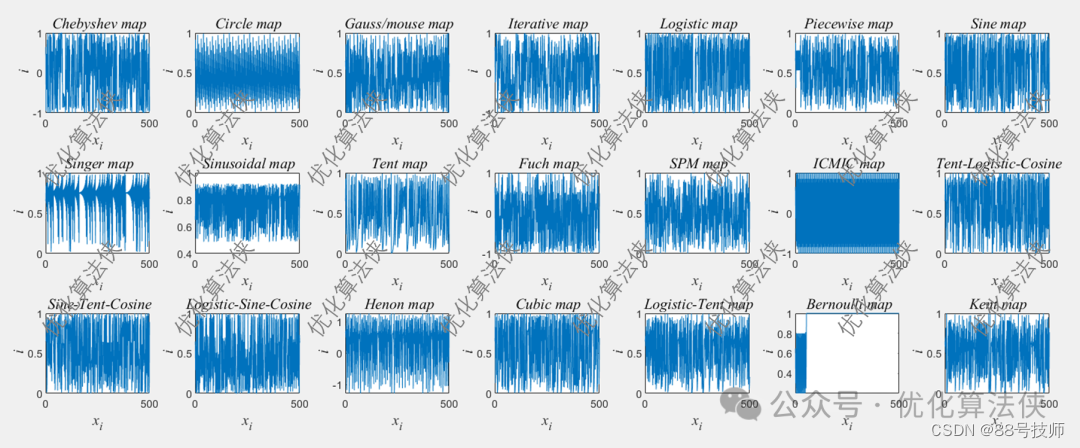
1. Chebyshev 混沌映射
![]()
Chebyshev 混沌映射原理简单,是常用的混沌映射之一。a阶Chebyshev混沌映射表达式为:
![]()
其中a通常取值为4。混沌轨道状态值范围为(-1,1)。
2. Circle 混沌映射
![]()
Circle混沌映射有着随机性,均匀性和有序性等特点。Circle映射可表示为:
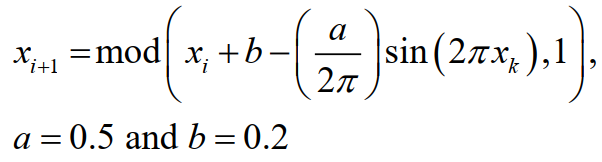
其中,a,b为控制参数,常用的取值为0.5和0.2,mod为求余函数。混沌轨道状态值范围为(0,1)。
3. Gauss/mouse 混沌映射
![]()
Gauss/mouse混沌映射是常用的混沌映射之一,其表达式为:
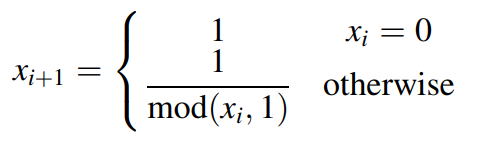
混沌轨道状态值范围为(0,1)。
4. Iterative 混沌映射
![]()
lterative 混沌映射的数学表达式为:
![]()
a为控制参数,在(0,1)中取值,一般为0.7。混沌轨道状态值范围为(-1,1)。
5. Logistic 混沌映射
![]()
Logistic混沌映射原理简单,具有较强的随机性和遍历性,是常用的混沌映射之一。混沌映射表达式为
![]()
其中,a为控制参数,在(0,4]中取值,a越大混沌性越高,a=4时处于完全混沌状态。混沌轨道状态值范围为(0,1)。
6. Piecewise混沌映射
![]()
Piecewise混沌映射具有很好的统计性能,是一个分段映射函数。混沌映射公式为:
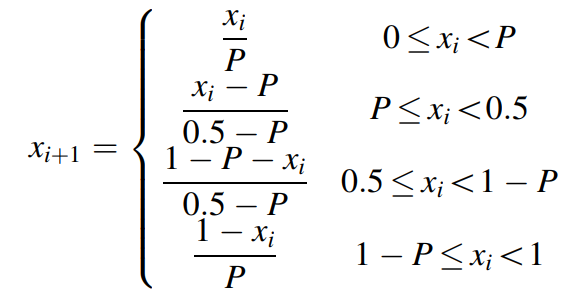
其中,P在 [0,0.5]内取值,为一个分段控制因子,用来划分该分段函数的4部分函数。一般d=0.3。混沌轨道状态值范围为(0,1)。
7. Sine 混沌映射
![]()
Sine混沌映射的表达式为:
![]()
其中a为控制参数,一般为4。混沌轨道状态值范围为(0,1)。
8. Singer 混沌映射
![]()
Singer映射是混沌映射的典型代表,它的数学形式很简单。其表达式如下:
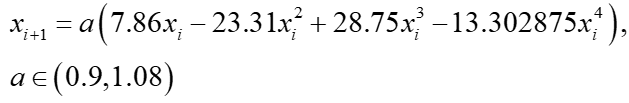
其中a为控制参数。混沌轨道状态值范围为(0,1)。
9. Sinusoidal 混沌映射
![]()
Sinusoidal混沌映射的数学表达式为:
![]()
其中a为控制参数,通常为2.3。混沌轨道状态值范围为(0,1)。
10. Tent 混沌映射
![]()
Tent映射又称为帐篷映射,其数学表达式为:
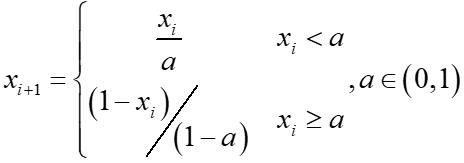
当a=0.5的时候,系统呈现短周期状态。当系统初值与a相同,系统将演化成周期系统。因此,使用时需注意以上两种特殊情况。混沌轨道状态值范围为(0,1)。
11. Fuch混沌映射
![]()
Fuch混沌映射使得优化结果不依赖于初始值,其表达式为:
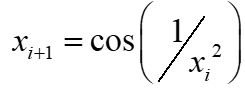
混沌轨道状态值范围为(-1,1)。
12. SPM混沌映射
![]()
SPM 映射函数定义:
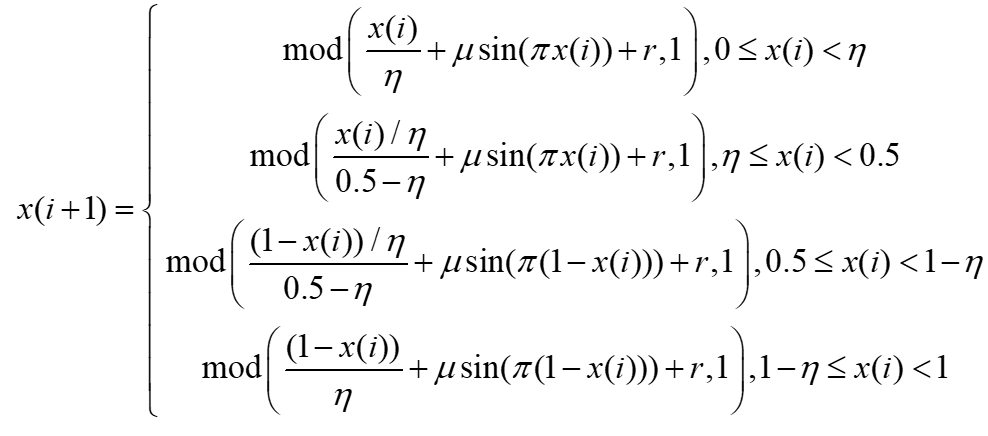
其中,r为0~1之间的随机数。当η∈(0,1)且μ∈(0,1)时,该函数处于混沌状态。实验表明当η=0.4且μ=0.3时,SPM映射产生的序列具有更好的遍历性和随机性。其混沌轨道状态值范围为(0,1)。
13. ICMIC混沌映射
![]()
ICMIC映射是一种映射折叠次数无线的混沌模型,相较于Logistic 映射和Tent映射,该映射具有遍历均匀和收敛较快等优点。ICMIC映射的数学表达式如下:
![]()
其中,a为控制参数,取值在(0,+∞)。其混沌轨道状态值范围为(-1,1)。
14. Tent-Logistic-Cosine混沌映射
![]()
组合运算可以有效地对两个种子映射的混沌动力学进行集合,余弦变换表现出非常复杂的非线性。因此,Tent-Logistic-Cosine产生的新的混沌映射具有复杂的行为:
![]()
其混沌轨道状态值范围为(0,1)。
15. Sine-Tent-Cosine混沌映射
![]()
Sine-Tent-Cosine混沌映射同样是组合混沌映射,表达式为:
![]()
其混沌轨道状态值范围为(0,1)。
16. Logistic-Sine-Cosine混沌映射
![]()
Logistic-Sine-Cosine混沌映射同样是组合混沌映射,表达式为:
![]()
其混沌轨道状态值范围为(0,1)。
17. Henon混沌映射
![]()
Henon混沌映射在2维空间产生,是一种典型的离散混沌映射,其动力学公式如下:
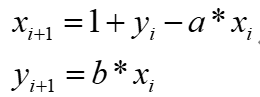
其中,a和b 参数决定Henon映射的状态,较1维混沌映射更复杂。研究结果表明:当a=1.4,b=0.3时,函数进入混沌状态,生成的混沌序列具有很强的随机性。其混沌轨道状态值范围为(-1.5,1.5)。
18. Cubic混沌映射
![]()
相比 Logistic混沌映射,Cubic混沌映射具较好的混沌遍历性,有寻优速度快﹑精度高的特点。表达式如下:
![]()
取a=2.595的混沌参数,Cubic混沌映射在(0.1)之间具有较好的遍历性。
19. Logistic-Tent映射
![]()
将经典一维Logistic系统、Tent混沌系统进行集成生成的Logistic-Tent复合混沌系统。该混沌系统融合了Logistic复杂的混沌动力学特性和Tent混沌系统更快的迭代速度、更多的自相关性和适用于大量序列的特点。它的数学公式定义如下:
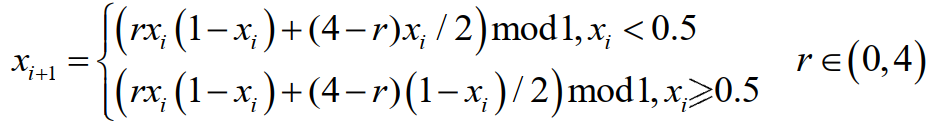
其混沌轨道状态值范围为(0,1)。
20. Bernoulli 混沌映射
![]()
Bernoulli映射表达式为:
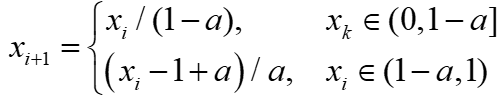
其中,a为控制参数。其混沌轨道状态值范围为(0,1)。
21. Kent映射
![]()
Kent映射是另一个具有代表性且形式简单的离散混沌系统,从数学上讲,Kent映射与Logistic 映射是同构的,因此Kent映射也可用于随机优化算法中生成随机新解的方法,而Kent映射具有比 Logistic映射更好的均匀遍历性。Kent映射系统方程可表为如下形式:
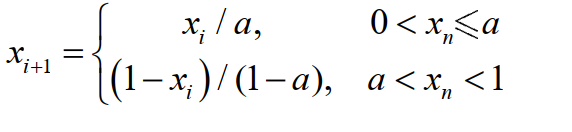
控制参数a∈(0,1)。混沌轨道状态值范围为(0,1)。
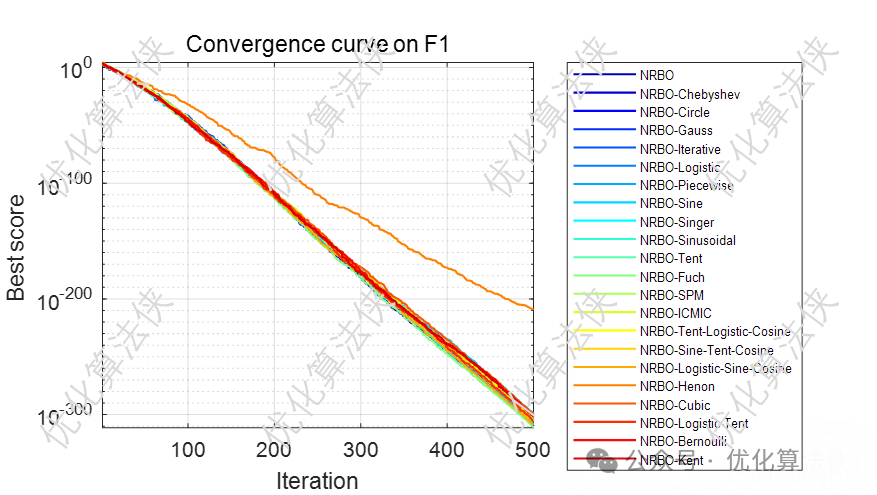
结果展示:
首先,对上述21种混沌映射方法,进行分布上的遍历。可以清楚看到他们不同的特征。
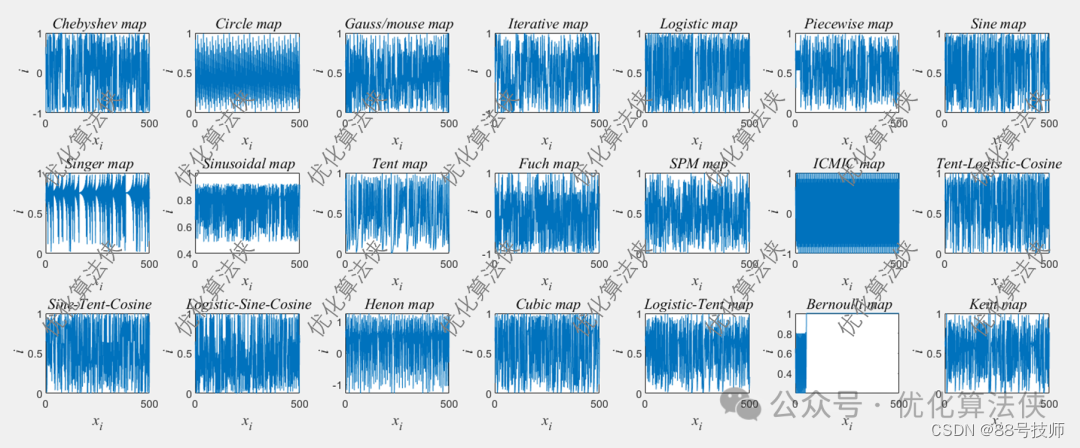
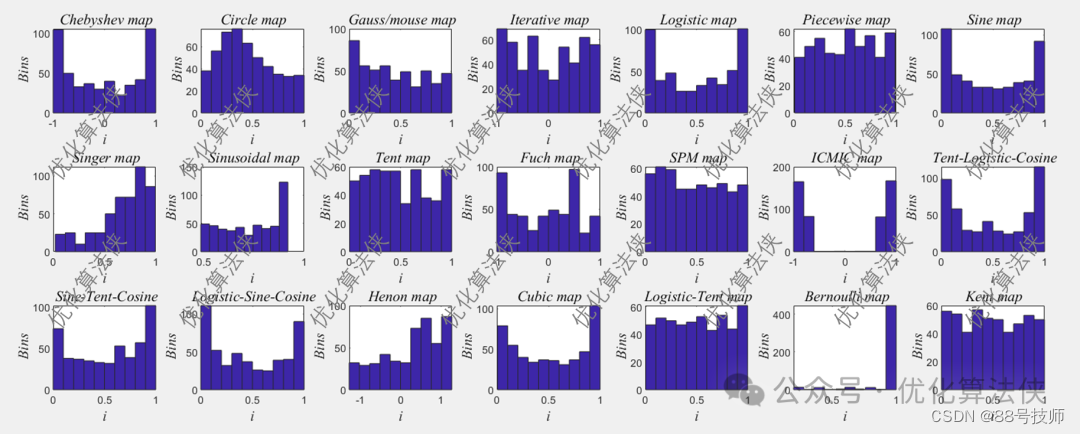
其次,将他们运用到种群初始化中。以2024年的最新算法2024年优化算法-牛顿-拉夫逊优化算法Newton-Raphson-based optimizer(附Matlab代码)为例。在cec2005上对比21种混沌改进策略。