算法基础原理
贪心算法是一种在求解问题时,总是做出在当前看来是最好的选择的算法。它不从整体最优上进行考虑,而是通过每一步的局部最优选择,希望达到全局的最优解.
贪心算法的特点:贪心算法在每一步都选择当前状态下的最优解,即局部最优解,同时贪心算法采用自顶向下的方式,以迭代的方法做出相继的贪心选择,每做一次贪心选择,就将所求问题简化为一个规模更小的子问题。虽然每一步都保证能获得局部最优解,但由此产生的全局解有时不一定是最优的,所以贪心算法不要回溯。
贪心算法包含以下几种分支:
- 标准贪心算法:
- 活动选择问题:选择最大数量的不重叠活动。
- 埃及分数问题:将真分数表示为一系列不重复的倒数之和。
- 霍夫曼编码:用于数据压缩,构建最优前缀码。
- 水连接问题:用最少的管子连接所有的房子。
- 图中的贪心算法:
- Kruskal的最小生成树算法:通过不断加入最小的边来构建最小生成树。
- Prim的最小生成树算法:从一个顶点开始,每次加入连接已选顶点和未选顶点之间的最小边。
- Dijkstra的最短路径算法:用于找到图中单源最短路径。
- 数组中的贪心算法:
- 数组的最小乘积子集问题:选择数组中某些数,使得它们的乘积最小。
- 最大化数组总和问题:在限定操作次数下最大化数组的总和。
- 其他与数组相关的最大化或最小化问题,如最大化连续差异的总和等。
贪心算法的基础流程如下:
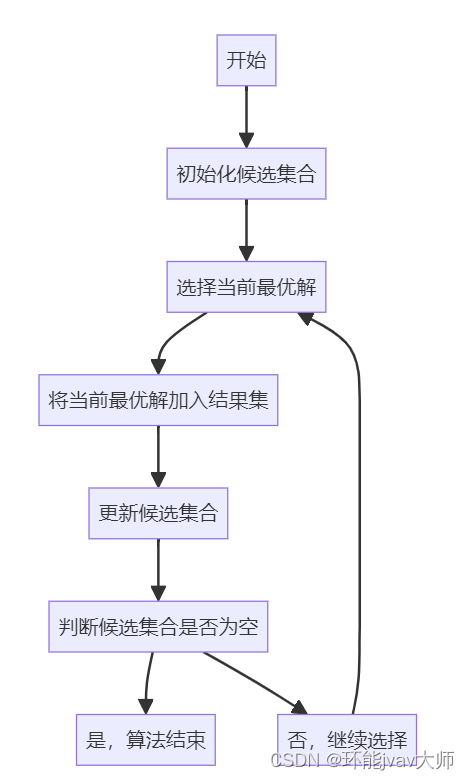
代码实现
金钱找零
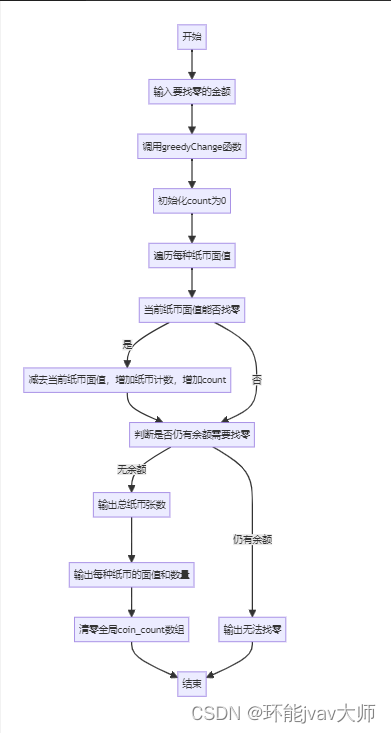
先定义一个包含四种面值纸币的数组coins和一个记录每种硬币数量的数组coin_count。greedyChange函数接收一个整数money作为输入,表示需要找零的金额。函数通过遍历coins数组,从最大面值的纸币开始,尽可能多地使用每种面值的纸币,直到找零完成或无法找零。如果找零成功,它会打印出总共需要的纸币数量和每种面值纸币的数量;如果无法找零,它会打印出“无法找零”。最后main函数从用户那里获取要找零的金额,并调用greedyChange函数进行处理。
#include <stdio.h> // 定义可用纸币面值 int coins[] = {20, 10, 5, 1}; #define NUM_COINS 4 // 定义需要纸币的数量 int coin_count[NUM_COINS] = {0}; // 设置一个全局变量用于记录每种硬币的数量 void greedyChange(int money) { int i, count = 0; for (i = 0; i < NUM_COINS; i++) { // 使用NUM_COINS宏 while (money >= coins[i]) { money -= coins[i]; coin_count[i]++; // 修改全局变量,不需要前缀global_ count++; } } if (money != 0) { printf("无法找零\n"); return; } printf("总共需要 %d 张money\n", count); for (i = 0; i < NUM_COINS; i++) { if (coin_count[i] != 0) { printf("面值 %d 的纸币需要 %d 张\n", coins[i], coin_count[i]); } } // 清零全局的coin_count数组以供下次使用 for (i = 0; i < NUM_COINS; i++) { coin_count[i] = 0; } } int main() { int money; printf("请输入要找零的金额: "); scanf("%d", &money); greedyChange(money); return 0; }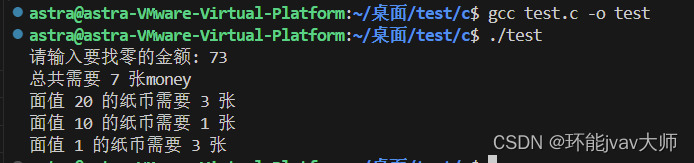
计算连续插值的最大和
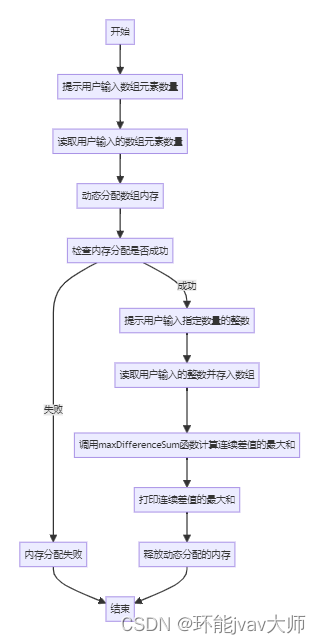
先提示用户输入数组元素的数量,并动态分配相应大小的内存来存储这些元素。接着要求用户输入指定数量的整数,并将这些整数存储在之前分配的数组中。然后调用maxDifferenceSum函数来计算数组中任意两个连续元素之间差值的绝对值之和的最大值。这个函数通过两层循环遍历数组,外层循环确定起始位置,内层循环计算从当前起始位置到数组末尾的所有连续差值的绝对值之和,并在过程中更新最大和。最后打印出连续差值的最大和,并释放之前动态分配的内存。
#include <stdio.h> #include <stdlib.h> #include <math.h> int maxDifferenceSum(int arr[], int n) { int maxSum = 0; for (int i = 0; i < n; i++) { int currentSum = 0; for (int j = i; j < n - 1; j++) { currentSum += abs(arr[j] - arr[j + 1]); if (currentSum > maxSum) { maxSum = currentSum; } } } return maxSum; } int main() { int n; printf("请输入数组元素的数量: "); scanf("%d", &n); // 动态分配数组内存 int *arr = (int *)malloc(n * sizeof(int)); if (arr == NULL) { printf("内存分配失败!\n"); return 1; } printf("请输入 %d 个整数:\n", n); for (int i = 0; i < n; i++) { scanf("%d", &arr[i]); } int result = maxDifferenceSum(arr, n); printf("连续差值的最大和为: %d\n", result); // 释放动态分配的内存 free(arr); return 0; }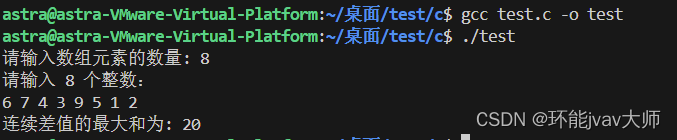
流程图的Markdown mermaid代码
基础流程:
graph TB A[开始] B[初始化候选集合] C[选择当前最优解] D[更新候选集合] E[判断候选集合是否为空] F[是,算法结束] G[否,继续选择] H[将当前最优解加入结果集] A --> B B --> C C --> H H --> D D --> E E --> F E --> G G --> CC语言实现找零钱流程:
graph TB A["开始"] B["输入要找零的金额"] C["调用greedyChange函数"] D["初始化count为0"] E["遍历每种纸币面值"] F["当前纸币面值能否找零"] G["减去当前纸币面值,增加纸币计数,增加count"] H["判断是否仍有余额需要找零"] I["输出无法找零"] J["输出总纸币张数"] K["输出每种纸币的面值和数量"] L["清零全局coin_count数组"] M["结束"] A --> B B --> C C --> D D --> E E --> F F -->|是| G G --> H F -->|否| H H -->|仍有余额| I H -->|无余额| J J --> K K --> L L --> M I --> MC语言计算连续插值的最大和
graph TB A[开始] B[提示用户输入数组元素数量] C[读取用户输入的数组元素数量] D[动态分配数组内存] E[检查内存分配是否成功] F[内存分配失败] G[提示用户输入指定数量的整数] H[读取用户输入的整数并存入数组] I[调用maxDifferenceSum函数计算连续差值的最大和] J[打印连续差值的最大和] K[释放动态分配的内存] L[结束] A --> B B --> C C --> D D --> E E --> |成功| G E --> |失败| F F --> L G --> H H --> I I --> J J --> K K --> L