
目录
🌈嗨!我是Filotimo__🌈。很高兴与大家相识,希望我的博客能对你有所帮助。
💡本文由Filotimo__✍️原创,首发于CSDN📚。
📣如需转载,请事先与我联系以获得授权⚠️。
🎁欢迎大家给我点赞👍、收藏⭐️,并在留言区📝与我互动,这些都是我前进的动力!
🌟我的格言:森林草木都有自己认为对的角度🌟。

前言
数据结构指的是计算机科学中用来组织和存储数据的方式,涉及数据元素之间的关系及其操作定义。数据结构可以分为线性结构和非线性结构。其中,线性结构是指数据元素之间存在一对一的关系,包括数组、链表、栈和队列等。
一、数组(Array)
数组是一种在内存中连续存储多个相同类型元素的数据结构。数组通过索引(通常从0开始)来访问每个元素。
示例代码(以下所有代码都是用C语言编写的)
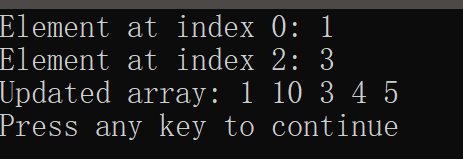
#include <stdio.h> #define SIZE 5 int main() { // 创建一个整数数组 int arr[SIZE] = {1, 2, 3, 4, 5}; // 访问数组元素 printf("Element at index 0: %d\n", arr[0]); // 输出: 1 printf("Element at index 2: %d\n", arr[2]); // 输出: 3 // 修改数组元素 arr[1] = 10; printf("Updated array: "); for (int i = 0; i < SIZE; ++i) { printf("%d ", arr[i]); } printf("\n"); return 0; }运行截图
1.1优点
① 快速访问:由于元素在内存中连续存储,可以通过索引直接访问任何元素,时间复杂度为 O(1)。
② 简单:实现简单直观,是最基础的数据结构之一。
1.2缺点
① 固定大小:数组创建时大小固定,通常无法动态扩展,需要预先确定容量。
② 插入和删除操作慢:在数组中间或开头插入或删除元素需要移动其他元素,时间复杂度为 O(n)。
1.3适用场景
数组适合于元素类型固定、需要频繁访问元素且不需要经常插入或删除元素的场景。
二、链表(Linked List)
链表是一种非连续、非顺序的数据结构,由节点组成,每个节点包含数据和指向下一个节点的指针(或引用)。根据指针的指向,链表能形成不同的结构,例如单链表,双向链表,循环链表等。
示例代码
#include <stdio.h> #include <stdlib.h> // 定义链表节点结构 typedef struct Node { int data; struct Node* next; } Node; // 创建一个新的节点 Node* create_node(int data) { Node* new_node = (Node*)malloc(sizeof(Node)); // 分配内存 new_node->data = data; new_node->next = NULL; return new_node; } // 向链表末尾添加节点 void append(Node** head_ref, int new_data) { Node* new_node = create_node(new_data); Node* last = *head_ref; if (*head_ref == NULL) { *head_ref = new_node; return; } while (last->next != NULL) { last = last->next; } last->next = new_node; } // 打印链表 void print_list(Node* node) { while (node != NULL) { printf("%d -> ", node->data); node = node->next; } printf("NULL\n"); } // 释放链表内存 void free_list(Node* node) { Node* temp; while (node != NULL) { temp = node; node = node->next; free(temp); } } int main() { Node* head = NULL; // 创建链表 append(&head, 1); append(&head, 2); append(&head, 3); append(&head, 4); // 打印链表 printf("Linked List: "); print_list(head); // 释放链表 free_list(head); return 0; }运行截图

2.1优点
① 动态大小:链表可以动态地分配内存空间,不像数组需要预先分配固定大小的空间。
② 插入和删除快速:在链表中插入和删除元素不需要移动其他元素,只需要改变指针指向,时间复杂度为 O(1)。
2.2缺点
① 随机访问慢:链表的元素不连续存储,访问特定位置的元素需要从头开始遍历,时间复杂度为 O(n)。
② 额外空间:每个节点除了存储数据外,还需存储指针,占用较多的内存空间。
2.3适用场景
链表适合于需要频繁插入和删除操作、内存空间不确定或者不需要随机访问元素的场景。
三、栈(Stack)
栈是一种特殊的线性表,具有后进先出(LIFO,Last In First Out)的特点,只允许在一端进行插入和删除操作。这一端被称为栈顶,另一端称为栈底。
示例代码
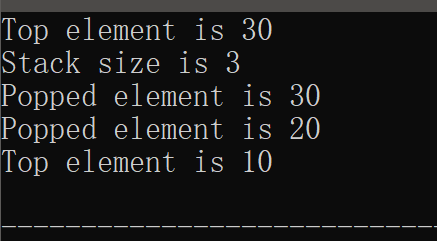
#include <stdio.h> #include <stdlib.h> #define MAX_SIZE 100 // 栈的最大容量 // 定义栈结构体 typedef struct { int items[MAX_SIZE]; int top; // 栈顶指针 } Stack; // 初始化栈 void init(Stack* stack) { stack->top = -1; // 栈顶指针初始化为-1,表示栈为空 } // 判断栈是否为空 int is_empty(Stack* stack) { return stack->top == -1; } // 判断栈是否已满 int is_full(Stack* stack) { return stack->top == MAX_SIZE - 1; } // 入栈操作 void push(Stack* stack, int item) { if (is_full(stack)) { printf("Stack overflow\n"); return; } stack->items[++stack->top] = item; // 栈顶指针先加一,然后添加元素 } // 出栈操作 int pop(Stack* stack) { if (is_empty(stack)) { printf("Stack underflow\n"); return -1; // 返回-1表示出栈失败 } return stack->items[stack->top--]; // 返回栈顶元素,并将栈顶指针减一 } // 查看栈顶元素 int peek(Stack* stack) { if (is_empty(stack)) { printf("Stack is empty\n"); return -1; // 返回-1表示栈为空 } return stack->items[stack->top]; // 仅返回栈顶元素,不改变栈的状态 } // 获取栈的大小 int size(Stack* stack) { return stack->top + 1; } int main() { Stack stack; init(&stack); // 初始化栈 push(&stack, 10); push(&stack, 20); push(&stack, 30); printf("Top element is %d\n", peek(&stack)); // 输出: 30 printf("Stack size is %d\n", size(&stack)); // 输出: 3 printf("Popped element is %d\n", pop(&stack)); // 输出: 30 printf("Popped element is %d\n", pop(&stack)); // 输出: 20 printf("Top element is %d\n", peek(&stack)); // 输出: 10 return 0; }运行截图
3.1优点
① 操作简单:只允许在栈顶进行插入和删除操作,实现简单直观。
② 内存管理方便:栈的内存管理由系统自动处理,无需程序员手动管理。
3.2缺点
① 容量限制:栈的大小受限于系统内存的大小,可能会造成栈溢出。
② 不支持随机访问:由于只能操作栈顶元素,无法直接访问栈中间的元素。
3.3适用场景
① 递归算法(如深度优先搜索)
② 表达式求值(如逆波兰表达式)
③ 括号匹配(如编译器的语法分析)
④ 历史记录(如浏览器前进后退功能)
⑤ 撤销操作(如文本编辑器的撤销功能)
四、队列(Queue)
队列是一种具有先进先出(FIFO,First In First Out)特性的数据结构,允许在一端插入(enqueue)元素,另一端删除(dequeue)元素。通常用于需要按顺序处理数据的场景。
示例代码
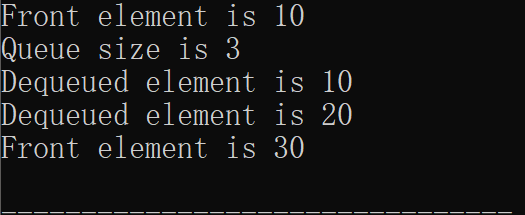
#include <stdio.h> #include <stdlib.h> #define MAX_SIZE 100 // 队列的最大容量 // 定义队列结构体 typedef struct { int items[MAX_SIZE]; int front; // 队头指针 int rear; // 队尾指针 int size; // 队列当前元素个数 } Queue; // 初始化队列 void init(Queue* queue) { queue->front = 0; queue->rear = -1; queue->size = 0; } // 判断队列是否为空 int is_empty(Queue* queue) { return queue->size == 0; } // 判断队列是否已满 int is_full(Queue* queue) { return queue->size == MAX_SIZE; } // 入队操作 void enqueue(Queue* queue, int item) { if (is_full(queue)) { printf("Queue overflow\n"); return; } queue->rear = (queue->rear + 1) % MAX_SIZE; // 环形队列实现 queue->items[queue->rear] = item; queue->size++; } // 出队操作 int dequeue(Queue* queue) { if (is_empty(queue)) { printf("Queue underflow\n"); return -1; // 返回-1表示出队失败 } int dequeued_item = queue->items[queue->front]; queue->front = (queue->front + 1) % MAX_SIZE; // 环形队列实现 queue->size--; return dequeued_item; } // 查看队头元素 int peek(Queue* queue) { if (is_empty(queue)) { printf("Queue is empty\n"); return -1; // 返回-1表示队列为空 } return queue->items[queue->front]; } // 获取队列的大小 int size(Queue* queue) { return queue->size; } int main() { Queue queue; init(&queue); // 初始化队列 enqueue(&queue, 10); enqueue(&queue, 20); enqueue(&queue, 30); printf("Front element is %d\n", peek(&queue)); // 输出: 10 printf("Queue size is %d\n", size(&queue)); // 输出: 3 printf("Dequeued element is %d\n", dequeue(&queue)); // 输出: 10 printf("Dequeued element is %d\n", dequeue(&queue)); // 输出: 20 printf("Front element is %d\n", peek(&queue)); // 输出: 30 return 0; }运行截图
4.1优点
① 按序处理:队列确保元素按照入队的顺序处理,符合先进先出的逻辑。
② 操作简单:队列仅支持在队尾插入和队头删除操作,设计和实现都较为简单。
③ 资源管理:队列的大小可以动态增长,灵活适应不同数据量的需求。
4.2缺点
① 固定容量:队列的大小通常是固定的,可能会导致队列满时无法继续入队(队列溢出)。
② 不支持随机访问:只能访问队头元素,不能直接访问队列中间的元素。
4.3适用场景
① 任务调度:用于任务按顺序执行,例如操作系统中的进程调度。
② 消息传递:用于实现异步消息传递机制,例如消息队列中间件。
③ 广度优先搜索:在图的遍历中,广度优先搜索算法需要使用队列来管理遍历的节点顺序。
④ 缓冲:用于平衡生产者和消费者之间的速度差异,例如生产者消费者模型中的缓冲区。
⑤ 网络数据包处理:在网络数据传输中,使用队列来管理接收到的数据包。

