阅读量:2
【数据结构】堆的实现以及建堆算法和堆排序

🔥个人主页:大白的编程日记
🔥专栏:数据结构
文章目录
前言
哈喽,各位小伙伴大家好!上期给大家讲了树,二叉树以及堆。今天带着大家实现堆这个数据结构,以及堆排序。话不多说,咱们进入正题!向大厂冲锋!
一.堆的实现
- 堆的定义
我们用数组控制堆,在物理上是一个数组。逻辑上想象成堆。然后用size记录堆的节点个数。后面涉及扩容,所以用capacity记录数组空间大小。这里我们实现的是小堆
typedef int HPDataType; typedef struct Heap { HPDataType* a; int size; int capacity; }HP; - 堆的初始化
初始化时我们可以先给堆开好空间,也可以不开。我们不开就先给NULL,然后size和capacity都先给0。
void HPInit(HP* php) { assert(php); php->a = NULL; php->size = php->capacity = 0; }//初始化 - 堆的销毁
我们先free销毁数组,在把size和capacity置为0.
void HPDestroy(HP* php) { assert(php); free(php->a);//销毁数组 php->a = NULL; php->capacity = php->size = 0; }//销毁 1.1 堆数据的插入
- 思路分析
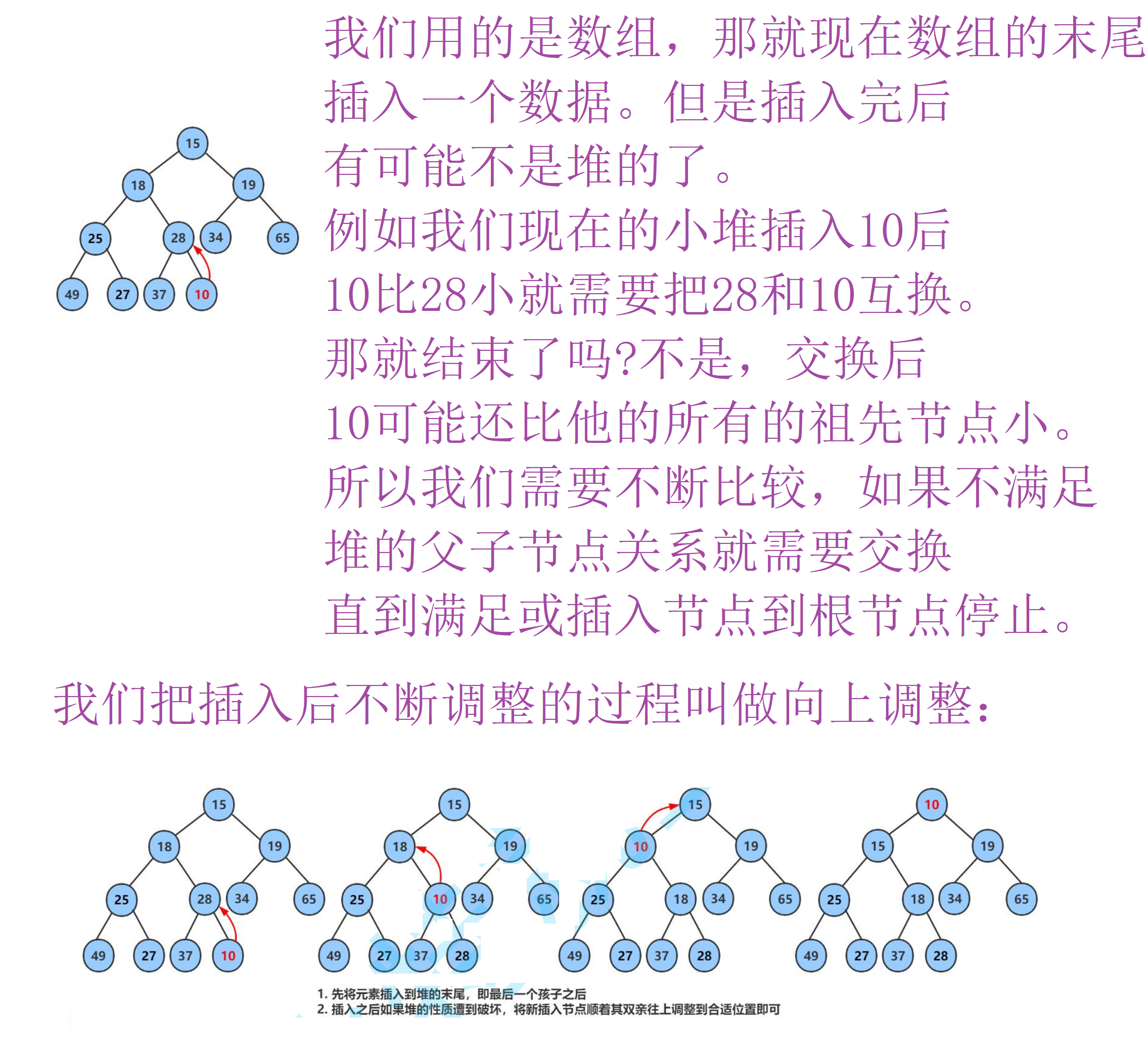
想要实现堆的插入,我们需要在数组插入数据后进行向上调整。
- 堆数据插入
插入数据前我们需要检查一下是否需要扩容。
第一次没开空间,我们就给4个数据的空间。
否则我们就realloc扩容为2倍。
最后在赋值。然后size++更新节点个数。
再用向上调整。
void HPPush(HP* php, HPDataType x) { assert(php);//断言 if (php->size == php->capacity)//空间满 { int newcapacity = php->capacity == 0 ? 4 : 2 * php->capacity; HPDataType* tmp = (HPDataType*)realloc(php->a, sizeof(HPDataType) * newcapacity); if (tmp == NULL) { perror("realloc fail~"); return; } php->a = tmp; php->capacity = newcapacity; } php->a[php->size++] = x;//插入 AdjustUp(php->a, php->size);//向上调整 } - 向上调整算法
我们size是数据个数,所以插入的child节点下标为size-1.那我们要找到他的父亲节点就是(child - 1) / 2。
然后判断插入数据和父亲节点的大小关系是否满足堆。
不满足就交换父子节点。然后更新child节点的下标。
满足则停止。或直到child节点到根节点时停止。
void AdjustUp(HPDataType* a, int size) { int child = size - 1;//最后的节点 while (child > 0) { int parent = (child - 1) / 2;//父亲节点 if (a[child] < a[parent])//判断 { Swap(&a[child], &a[parent]);//交换 child = parent; } else { break;//调整完成 } } } 1.2堆数据的删除
- 思路分析
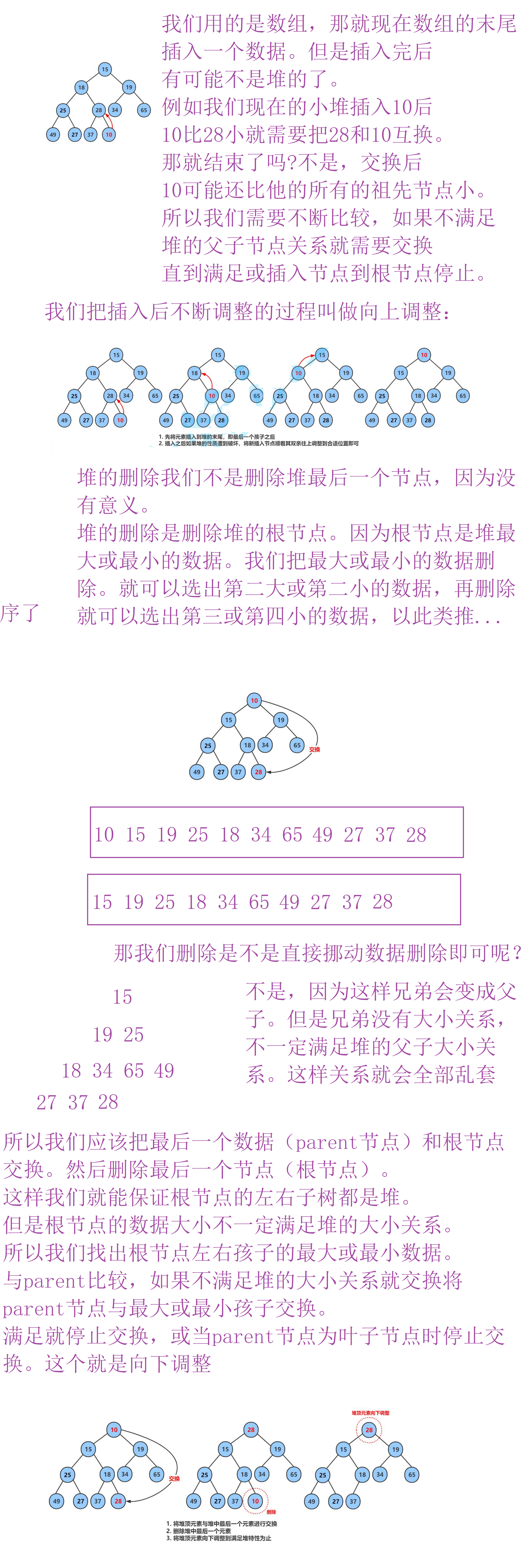
所以我们需要把最后一个节点和堆的根节点交换后,删除最后一个节点,然后向下调整。
- 堆数据的删除
我们先Swap交换根节点和最后一个节点,然后size–删除最后一个节点。再进行向下调整。
void HPPop(HP* php)//删除根节点 { assert(php); assert(php->size );//判断是否为空 Swap(&php->a[0], &php->a[php->size-1]);//交换根节点和最后一个节点 php->size--;//删除堆最后一个数据 AdjustDown(php->a,php->size,0);//向下调整 } - 向下调整算法
我们先算parent的左孩子child的下标。
然后用假设法找出左右孩子最大或最小的那个孩子,注意有可能只有左孩子没有右孩子。所以我们用min+1<size判断是否存在右孩子。然后再将找出的最大或最小孩子与parent节点进行比较。如果不满足堆的大小关系就交换,然后更新parent的下标和新的child的下标。
满足就break停止循环,或当child<=size说明此时parent为叶子节点停止循环。
void AdjustDown(HPDataType* a, int size,int parent) { int child = parent * 2 + 1;//孩子节点 while (child<size) { int min = child;//左右孩子中最小的孩子 if (min+1<size&&a[min] > a[min + 1])//防止没有右孩子 { min = child + 1; }//假设法 if (a[parent] > a[min])//判断 { Swap(&a[parent], &a[min]);//交换 parent = min; child = parent * 2 + 1; } else { break;//调整完毕 } } } - 堆的判空
直接判断是否size为0
bool HPEmpyt(HP* php) { assert(php); return php->size == 0;//判空 } - 堆的数据个数
直接返回size即可
int HPSize(HP* php) { assert(php); return php->size;//返回数据个数 } - 堆顶元素
直接返回下标为0的位置数据即可。
HPDataType HPTop(HP* php) { assert(php); assert(php->size);//判断是否为空 return php->a[0];//返回根节点 } 二.建堆算法和堆排序
现在我们要实现堆排序,那我们需要建堆。
那升序建大堆还是小堆,降序建大堆还是小堆呢?还是都可以呢?
升序建大堆 降序建小堆 为什么呢?
2.1思路分析

那如何建堆呢?
有两种建堆算法。
2.2向上建堆算法
我们堆插入的过程其实就是建堆的过程。
for (int i = 1; i < n; i++) { AdjustUp(p,i); } 
2.3向下调整建堆
我们从最后一个父亲节点依次往后向下调整
for (int i = (n - 1 - 1) / 2; i >= 0; i--) { AdjustDown(p, n, i); } 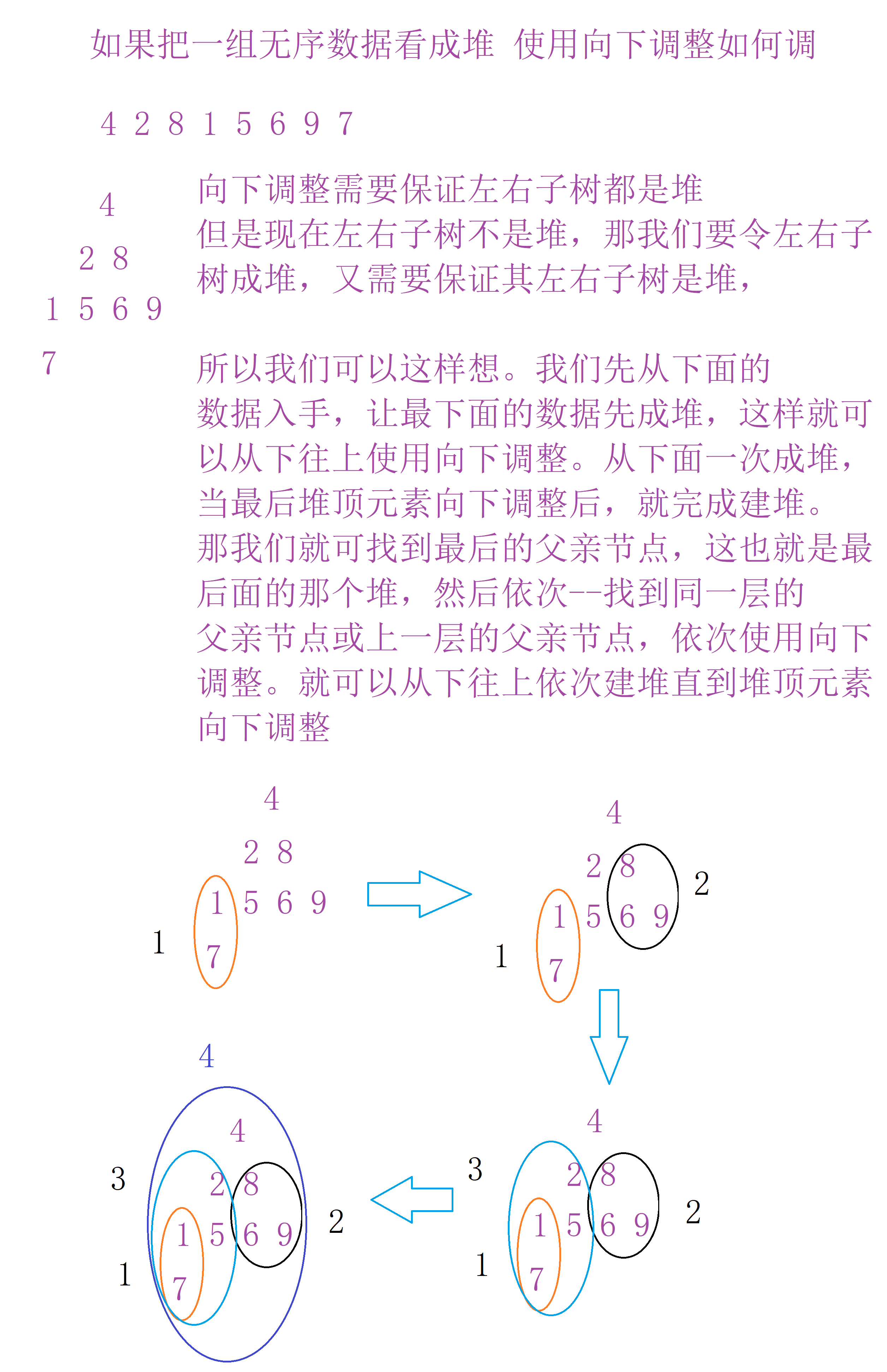
2.4堆排序
实现堆排序,我们升序建大堆,降序建小堆。
两种建堆算法都可以。
然后我们用end表示最后一个堆元素
每次循环交换堆顶元素和最后一个堆元素。
然后堆顶元素向下调整。更新最后一个堆元素即可。
void HeapSort(HPDataType* p, int n) { for (int i = 1; i < n; i++)//向上建堆 { AdjustUp(p,i); } int end = n - 1;//最后一个堆元素 while (end > 0)// { Swap(&p[0], &p[end]);//交换堆顶元素和最后一个堆元素 AdjustDown(p,end,0);//向下调整 end--;//更新最后一个堆元素 } } - 验证
void HeapSort(HPDataType* p, int n) { for (int i = 1; i < n; i++)//向上建堆 { AdjustUp(p,i); } int end = n - 1;//最后一个堆元素 while (end > 0)// { Swap(&p[0], &p[end]);//交换堆顶元素和最后一个堆元素 AdjustDown(p,end,0);//向下调整 end--;//更新最后一个堆元素 } } void test2() { int a[] = { 9,6,4,7,10,5,3,1,2,8}; HeapSort(a, sizeof(a) / sizeof(a[0])); for (int i = 0; i < sizeof(a)/sizeof(a[0]); i++) { printf("%d ", a[i]); } } int main() { test2(); return 0; } 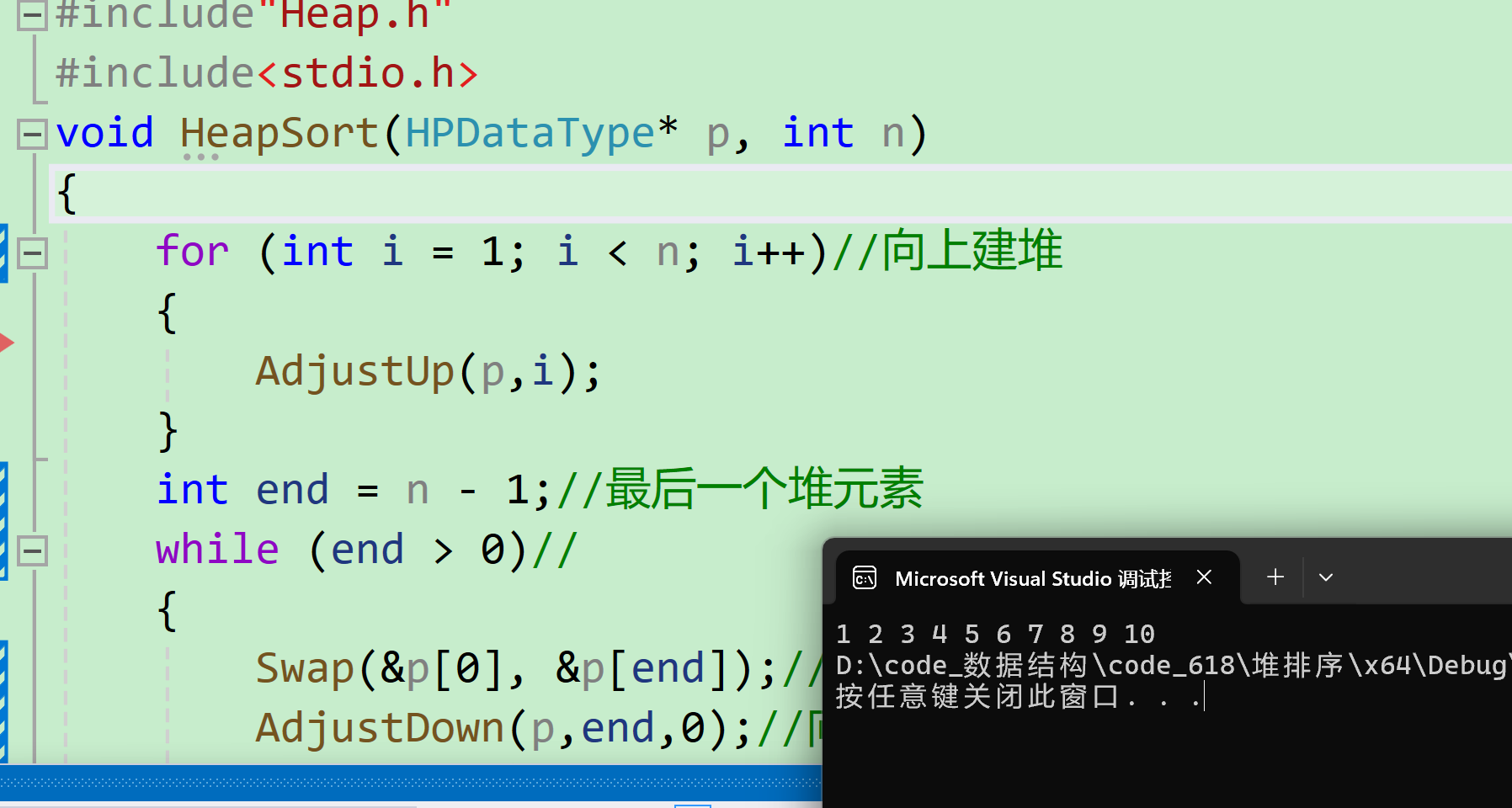
后言
这就堆的实现以及建堆算法和堆排序。这都是数据结构的重中之重。
大家一定要多加掌握。今天就分享到这,感谢各位大佬的耐心垂阅!咱们下期见!拜拜~


