目录
一.摘要
移动机器人路径规划一直是热门的研究领域,相关的算法丰富多样。本实践前期对机器人路径规划算法做了详细调研,检索并阅读了相关文献,了解了可视图法、人工势场法、启发式算法、神经网络算法等算法在机器人路径规划中的具体应用,本文采用强化学习中的 Q-learning 算法规划机器人的运动路径,做了算 法概念学习、算法代码设计、算法参数调优、算法训练测试等具体工作,查阅相 关开发资料后,决定应用 QT Creator 5.0.2 作为开发环境,采用栅格建模作为算 法应用情景、开发语言为 C++语言。
在完成上述算法设计和算法应用情景开发后,对算法进行仿真验证,训练次 数分别为 200、1000、5000 次,障碍物比例分别设置为 0.2、0.3、0.5,仿真后导 出数据绘制出普通折线图和堆积折线图,呈现结果,也发现了算法收敛速度慢、 初始次数搜索效率低等特点。 最后对本次实践做出总结和反思,对算法改进的方向做了描述,检索并阅读 了大量有关改进强化学习算法规划机器人运动路径的文献,对这些文献一一做了 简要概括。并且对本文算法的未来改进计划做出了初步设想。
关键词:移动机器人 路径规划 强化学习 Q-learning
二.路径规划技术的研究进展
1.研究现状
路径规划是指在规定区域内规划出一条从起始点到目标点的最优解路径,且 要保证与障碍物无碰撞。机器人路径规划存在的难点问题主要有环境建模问题、 算法收敛速度慢以及容易陷入局部最优解问题。[1]
2.算法分类
路径规划可以分为传统算法路径规划和智能仿生算法路径规划两类,其中传统路径规划算法又可以分为全局路径规划算法和局部路径规划算法。
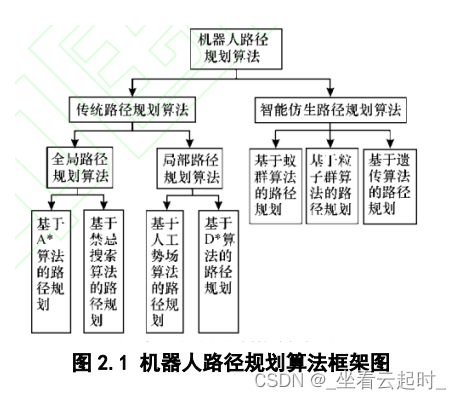
2.1 全局路径规划算法
全局路径规划算法主要包括可视图法、栅格法和自由空间法。
(1) 可视图法
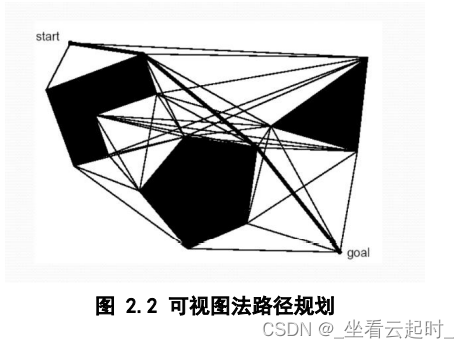
可视图法由 Lozano-Perez 和 Wesley 于 1979 年在论文:《An Algorithm for Planning Collision-Free Paths among Polyhedral Obstacles.》中提出。将机器人看作是一个 质点,障碍物看作是规则的多边形,分别把初始点、各多边形的各个顶点和目标 点之间用直线相连,直线不能穿过障碍物,这样得到的一张图即为可视图。[2] 再经过优化,把一些不必要的连线去掉,由出发点沿着所连的直线就可以到达目 标点,该路径就是一条无碰撞的可行路径,这就是可视图法。如图所示。
(2) 栅格法
采用正方形栅格表示环境,每个栅格有一个表征值 CV,表示在此方格中障 碍物对于机器人的危险程度,对于高 CV 值的栅格位置,机器人优先躲避,CV 值按其距机器人的距离被事先划分为若干等级。每个等级对机器人的躲避方向会 产生不同影响。
障碍物的位置一旦被确定,就按照一定的衰减方式赋给障碍物本身及其周围栅格一定的值,每个栅格的值代表了该位置有障碍物的可能性。栅格具有简单、 实用、操作方便的特点,完全能够满足使用要求。
(3) 自由空间法
主要思想是把障碍物按照一定的比例进行扩大,再把机器人按照合适比例缩小,再用设定好的凸多边形来描述机器人和环境,以此来解决路径规划问题,优点是构建连通图方便,缺点是当障碍物比较多的时候,算法复杂度较高,运行效率低下。
2.2 局部路径规划算法
2.2.1启发式算法
(1)遗传算法
Holland 于 1975 年首次提出遗传算法,是模仿生物进化中的基因遗传和优胜劣汰等过程的一种仿生学优化搜索算法。遗传算法通过模拟一个人工种群进化过程,通过选择( Selection) 、交 叉 ( Crossover) 以及变异( Mutation) 等机制,不断迭代搜索出近似最优解,进而达到求解的目的。 遗传算法进行搜索时首先要对种群进行初始化,而且需要确定问题求解的编码和解码过程,一般情况下采取实数编码或二进制编码,对于每一次迭代过程,遗传算法需要计算个体的适应度,也就是个体对于问题的匹配程度。适应度的值越大,解的质量就越高。 每一次迭代,种群需要经历选择、交叉、变异三个步骤。选择即从种群中选出适应性较好的个体,淘汰适应性较差的个体传入下一代种群。交叉即对个体对中的基因序列进行交换,通过交叉,遗传算法对解的搜索能力得到有效提高。[3] 变异即对个体基因序列中的基因值进行变动,使得算法具有局部的随机搜索能力,并能够维持群体的多样性,防止算法出现过早收敛的情况。 在迭代次数或者种群中最优个体的适应度达到一定阈值后算法终止。种群中适应度最高的个体就 是求得的相对最优解。
(2)粒子群算法
粒子群算法是一种基于群智能的随机优化算法,于1995 年由Kennedy和Eberhart提出。 该算法具有高效并行、流程简单、易于编程实现等特点,适于非线性优化问题的求解。 其思想来源于对鸟群捕食行为的模拟,优化问题的潜在解通常称为“粒子”,粒子属性可通过位置、速度和适应度函数进行描述。
(3)蚁群算法
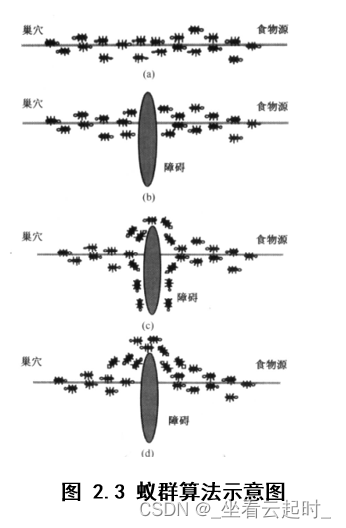
又称蚂蚁算法,是一种用来在图中寻找优化路径的机率型算法。它由Marco Dorigo于1992年在他的博士论文“Ant system: optimization by a colony of cooperating agents”中提出,其灵感来源于蚂蚁在寻找食物过程中发现路径的行为。蚁群算法是一种模拟进化算法,初步的研究表明该算法具有许多优良的性质。针对PID控制器参数优化设计问题,将蚁群算法设计的结果与遗传算法设计的结果进行了比较,数值仿真结果表明,蚁群算法具有一种新的模拟进化优化方法的有效性和应用价值。
2.2.2 神经网络算法
人工神经网络(Artificial Neural Networks,ANN)系统是 20 世纪 40 年代后出现的。它是由众多的神经元可调的连接权值连接而成,具有大规模并行处理、分布式信息存储、良好的自组织自学习能力等特点。BP(Back Propagation)算法又称为误差 反向传播算法,是人工神经网络中的一种监督式的学习算法。BP 神经网络算法在理论上可以逼近任意函数,基本的结构由非线性变化单元组成,具有很强的非线性映射能力。而且网络的中间层数、各层的处理单元数及网络的学习系数等参数可根据具体情况设定,灵活性很大,在优化、信号处理与模式识别、智能控制、故障诊断等许 多领域都有着广泛的应用前景。
2.2.3 人工势场法
人工势场实际上是对机器人运行环境的一种抽象描述。在势场中包含斥力和引力极,不希望机器人进入的区域的障碍物属于斥力极,子目标及建议机器人进入的区域为引力极。引力极和斥力极的周围由势函数产生相应的势场。机器人在势场中具有一定的抽象势能,它的负梯度方向表达了机器人系统所受到抽象力的方向,正是这种抽象力,促使机器人绕过障碍物,朝目标前进。人工势场法规划出的路径一般平滑且安全,结构简单、易于实现,但是有产生局部最优的问题。
三.本文采用的路径规划算法——强化学习
1.概念
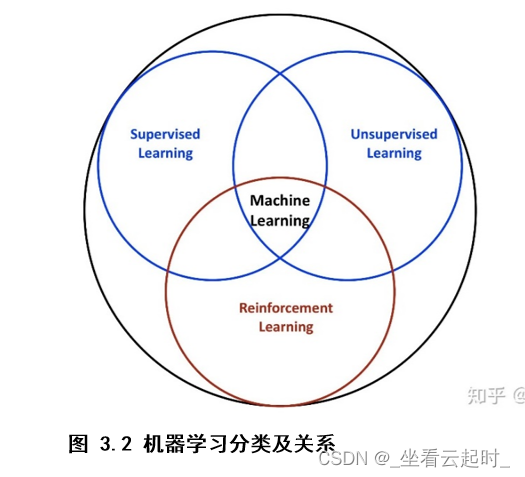
强化学习(Reinforcement Learning ,RL),是一种重要的机器学习方法,机器学习分为监督学习、无监督学习、强化学习三种。强化学习是系统从环境到行为映射的学习,目的是使奖励信号(强化信号)函数值最大。[4] 换句话说,强化学习是一种学习如何从状态映射到行为以使得获取的奖励最大的学习机制。一个动作需要不断在环境中进行实验,环境对动作做出奖励,系统通过环境的奖励不断优化行为,反复实验,延迟奖励。
2. 与其他机器学习方式的区别
也就是说与监督学习、无监督学习有什么不同之处。监督学习的训练集中,每一个样本都被打上标签,标签指代的是正确的结果。监督学习让系统按照每个样本所对应的标签推断出应有的反馈机制,进而在没有打过标签的样本上也能计算出正确结果。典型算法有:决策树、支持向量机(SVM)、k-近邻算法(KNN)等。无监督学习是从无标签的数据集中发现隐藏的结构,典型的例子就是聚类问题。常见算法有k-均值(K-means)、DBSCAN密度聚类算法、最大期望算法等。
强化学习在交互中不存在监督学习中的正确标签,而是在自身的经验中去学习。强化学习的目标也不是寻找隐藏的结构,而是最大化奖励。
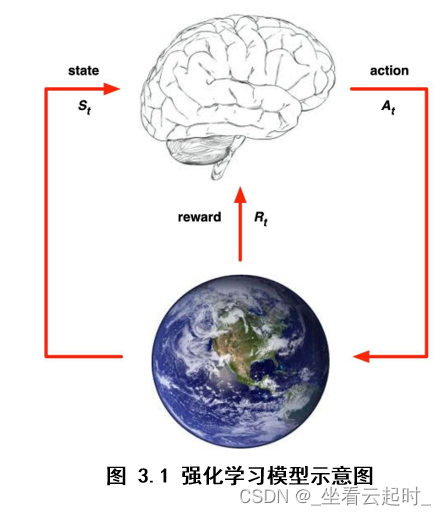
3. 强化学习模型
主体(Agent)通过与环境(environment)交互进行学习,交互包括行动(action),奖励(reward),状态(state)。交互过程表述如下:每一步主体都根据策略选择一个行动方式执行,比如说向前走、向后走,然后感知做出该行动后的立即奖励,还有下一步的状态,该状态也就是环境的状态,通过已有的经验再修改自己的策略做出下一个动作,经验就是根据这一步一步的动作学习来的,每一步都积累一些奖励值(立即奖励),目标就是让累积的奖励值最大。
假设主体所处的环境被描述为状态集S,可以执行的任意的动作集合A。下面描述强化学习模型运作过程:
强化学习系统(在主体上运作)接受环境状态的输入s,根据内部的推理机制,系统给出相应的动作a,环境在系统动作a下由s变迁到新的状态s’ ,系统再接受环境新状态的输入,同时得到环境对于系统刚才动作的立即奖励r。每次在某状态 下执行动作
下执行动作 ,主体会收到一个立即奖励
,主体会收到一个立即奖励 ,环境变迁到新的状态
,环境变迁到新的状态 。如此产生了一系列的状态
。如此产生了一系列的状态 ,动作
,动作 和立即奖励
和立即奖励 的集合,如图:
的集合,如图:
强化学习系统的目标是学习一个行为策略Π:S—>A,这个策略不是具体的某个动作,更像是一种决策的经验集合,根据这个策略,系统每一步都能做出让环境奖励累积值达到最大的动作。这个环境奖励累积值可以表示为: +γ
+γ +
+
 +…(0<=γ<1),其中γ为折扣因子,因为主体可能需要若干步才能到达目标,在这个过程中,每一步环境给主体的奖励是要打折扣的。
+…(0<=γ<1),其中γ为折扣因子,因为主体可能需要若干步才能到达目标,在这个过程中,每一步环境给主体的奖励是要打折扣的。
4.马尔可夫决策过程
上述对强化学习模型的描述其实就是马尔可夫决策过程,但是对一些值还要详细描述。环境给出的立即奖励 =r(
=r( ,
, ),产生后继状态函数
),产生后继状态函数 +1=ℳ(
+1=ℳ( ,
, ),该函数也叫状态转移函数。在马尔可夫决策过程中,r(
),该函数也叫状态转移函数。在马尔可夫决策过程中,r( ,
, )和ℳ(
)和ℳ( ,
, )只依赖于当前的动作和状态。
)只依赖于当前的动作和状态。
主体的任务是学习到策略Π:S—>A, (
( )=
)= 。该策略从初始状态
。该策略从初始状态 开始获得的累积奖励值为:
开始获得的累积奖励值为:
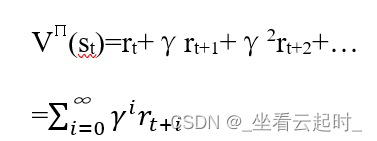
我们的目的是让上面的 (st)值最大,则这个策略就是最优策略,表示为
(st)值最大,则这个策略就是最优策略,表示为
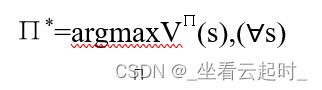
最优策略Π*的值函数为 *(s),记为V*(s)。V*(s)给出了当主体从状态s开始时可获得的最大折算累积回报。
*(s),记为V*(s)。V*(s)给出了当主体从状态s开始时可获得的最大折算累积回报。
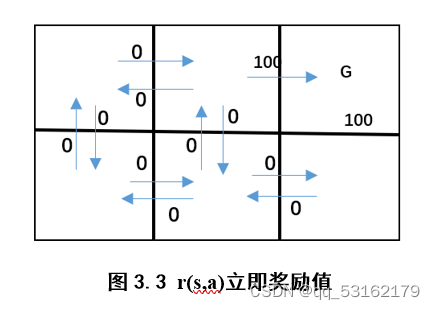
上图给出一个格状环境,每个箭头代表主体可采取的一个动作,从一个状态转移到另一个。每个箭头关联的数值代表主体执行该动作后的立即奖励r(s,a)。状态G可以看成是目标状态,主体只有进入该状态才有大于0的奖励值,进入其他状态的奖励值都为0,一旦主体进入G就只能留在其中。
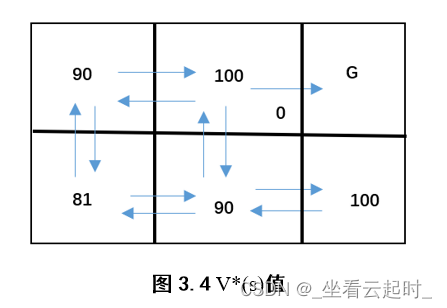
如图显示了每个状态的V*(s)值。假设γ=90,我们上面知道V*(s)给出了当主体从状态s(该格子)开始时可获得的最大折算累积回报,我们看下方中间的格子,它的V*(s)为90,从该格子走到目标状态的最优决策为先右后上(先上后右也一样),这时可计算出折算累积回报为0+γ*100+ *0+
*0+ *0+…=90,所以此格子用最优决策走到目标状态所能获得的最大累积回报就是90。
*0+…=90,所以此格子用最优决策走到目标状态所能获得的最大累积回报就是90。
5.Q-learning算法
Q-learning是强化学习的算法之一。Q-learning的主要目的就是学习状态动作价值函数的Q ( s , a ),其中Q ( s , a )表示的是在给定当前状态s和采取动作a之后能够获得的收益期望。Q-learning利用状态s和动作a张成一个Q表来储存Q值,然后根据Q值来选取能够获得最大收益的动作。Q-learning采用是值迭代的方法进行求解,其核心的迭代公式为
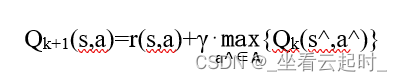
其中 ( s,a )是第k + 1次迭代函数,s和a分别表示的是当前的状态和执行的动作并且它们分别属于状态空间S和动作空间A,r ( s , a )表示的是在状态s执行动作a后的即时奖励,s^和a ^表示的是下一个的状态和行为,γ表示的是折扣系数。
( s,a )是第k + 1次迭代函数,s和a分别表示的是当前的状态和执行的动作并且它们分别属于状态空间S和动作空间A,r ( s , a )表示的是在状态s执行动作a后的即时奖励,s^和a ^表示的是下一个的状态和行为,γ表示的是折扣系数。

举个例子:
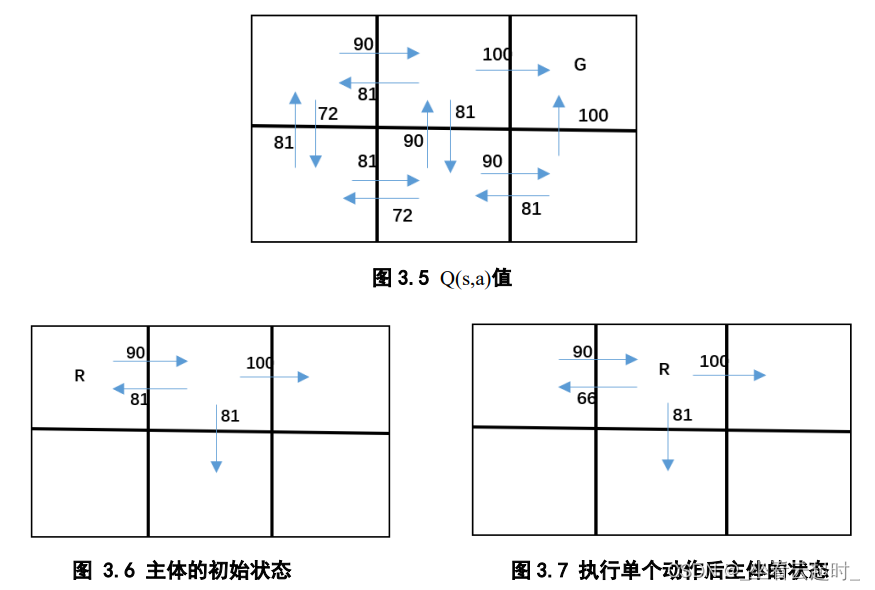
图3.6是主体的初始状态 和初始假设中几个相关的Q值,如Q(
和初始假设中几个相关的Q值,如Q( ,
, )=73,其中
)=73,其中 指代主体向右的动作。主体执行动作
指代主体向右的动作。主体执行动作 后,受到立即奖励为0,并转换到下一状态
后,受到立即奖励为0,并转换到下一状态 ,然后它基于对新状态
,然后它基于对新状态 的Q估计更新其Q(
的Q估计更新其Q( ,
, ),这里γ=0.9。
),这里γ=0.9。
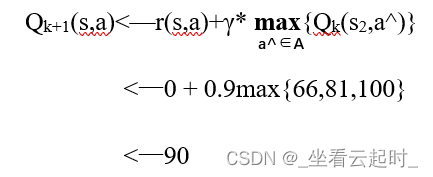
每次主体从旧状态前进到新状态,Q-learning会从新状态到旧状态向后传播其Q值。同时,主体收到的此转换的立即奖励被用于扩大这些传播的Q值,可以证明Q值在训练中永远不会下降。
Q的演化过程如下:初始Q值都为0,算法不会改变任何Q表项,直到它恰好到达目标状态并且收到非零奖励,这导致通向目标状态的转换的Q值被精化;在下一个情节中,如果经过这些与目标状态相邻的状态,那么其非零的Q值会导致与目的相差两步的状态中值的变化; 以此类推,最终得到一个Q表。
如果系统是一个确定性的马尔可夫决策过程,则立即奖励值都是有限的,主体选择动作的方式为它无限、频繁地访问所有可能的状态-动作对,那么算法会收敛到一个等于真实Q函数值的Q(近似)。
四.算法设计及代码实现
开发环境:Qt Creator 5.0.2 C++语言开发
参考了CSDN博主“榕林子”,“~在下小吴”的文章
程序架构等设计参考了榕林子的文章,链接如下:
文献[5]人工智能学习之机器人路径规划优化_榕林子的博客-CSDN博客_人工智能路径规划
算法设计参考了~在下小吴的文章,链接如下:
文献[6]基于Q-learning的无人机三维路径规划(含完整C++代码)_~在下小吴的博客-CSDN博客_无人机三维路径规划
程序架构:
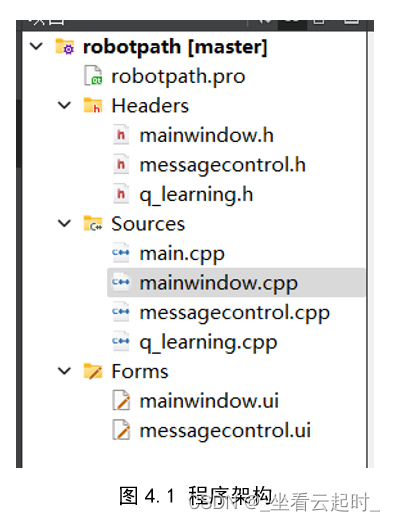
Mainwindow中放置了按钮的槽函数,以及强化学习的训练流程,控制的是主页面,Mainwindow.ui也是绘制的主页面,messagecontrol控制的是单元格,它的ui是绘制单元格的效果,messagecontrol.cpp中定义了鼠标事件函数和单元格颜色更改函数,q_learning不需要ui,里面定义了强化学习的action函数,用来控制机器人行动,定义了函数actpunish(),用来初始化一些特殊位置的Q值,定义了get_expected_max_reward(),用来返回下一步选择的最大Q值,也就是对应公式中的![]()
1.UI设计
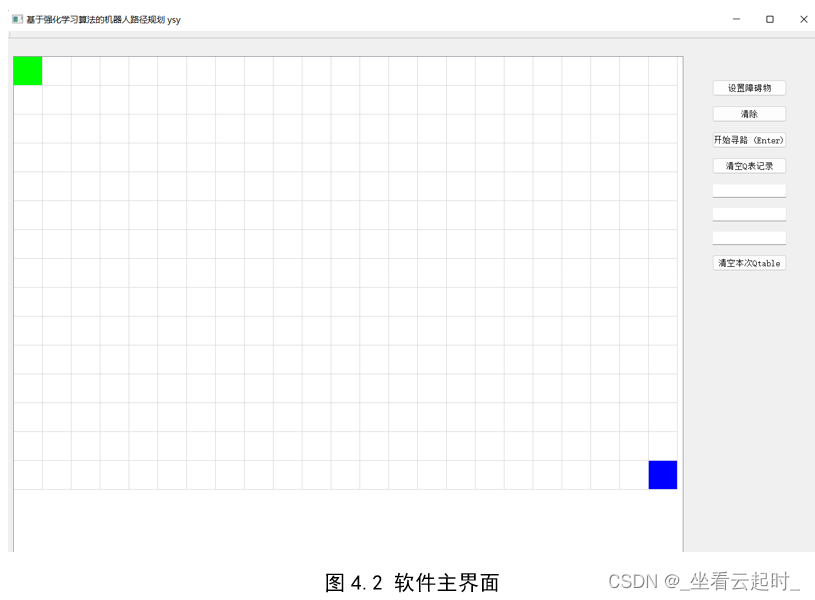
为机器人设置了行走的空间,以表格的形式展现,这里使用了控件TableWidget,分成23行,15列,但是第一行第一列的坐标都是从0开始,所以最后一个格子(右下角)的坐标是(22,14)。
这里注意,在手动设置UI时,要保证TableWidget足够大,否则在运行程序时,一部分表格会显示不全,我在开发程序的时候,想为起始点(0,0)设置颜色,弄了很长时间,换了好几种配置颜色的方式,都发现没效果,最后才发现是在.ui那个文件中,TableWidget不够大,遮挡了一部分格子。
画面右侧设置了几个按钮,逐一介绍:
(1)设置障碍物
鼠标点击单元格,可以选中变色,效果如下:
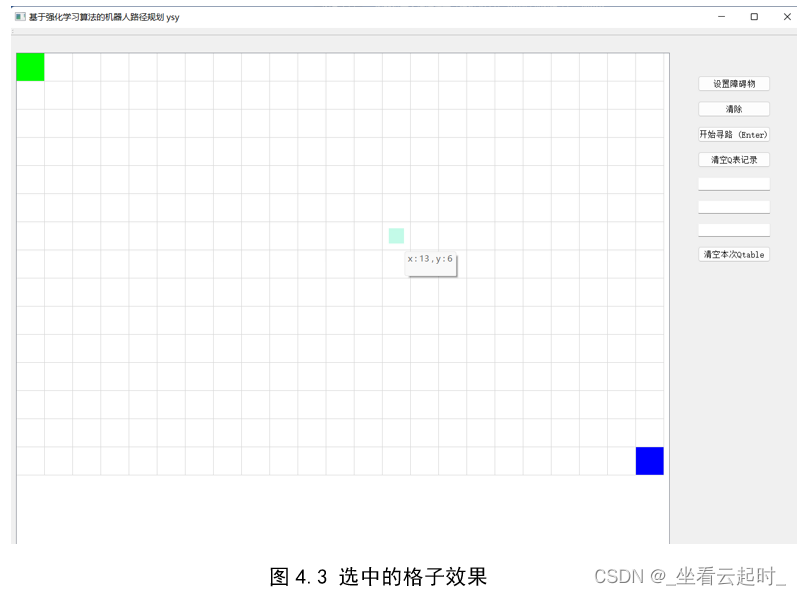
变色的格子就是鼠标点击选中的,如果后悔不想要选中这个,再点击一次,就可以取消,选中需要设置障碍物的格子之后,点击按钮“设置障碍物”,格子就会变成灰色,效果如下:

如果想改变障碍物位置,可以再点击一次格子,会从灰色变成刚才选中的状态,相当于取消了设置成障碍物。
(2)清除按钮
点击后可以清除所有的障碍物和行走轨迹。
(3)开始寻路
该按钮点击后,机器人从起始点出发开始寻径,按钮文字会从“开始寻路(Enter)”变为“停止寻路 (Enter)”,再次点击按钮,寻径就会暂停,可以随时切换状态。
(4)清空Q表记录
点击该按钮之后,本地记录Q表值的文本文件就会被清空,可以防止数据冗余,方便后续的算法测试。
此处代码用到Qfile里面的读写
1. QFile file("D:/Qt/project/robotpath/algorithmdata.txt"); 2. //对文件进行写操作 3. file.open(QIODevice::WriteOnly|QIODevice::Truncate); 4. file.close(); 这里面QIODevice::Truncate代表的是打开文件时清空文件所有内容。
(5)清空Qtable
后面训练要用到这个按钮,否则每次都要重新运行。
(6)剩余按钮
剩余三个按钮从上至下分别是“打印训练次数”、“打印步数”、“打印成功走到终点的总次数”。用的控件都是LineExit
“打印训练次数”是当训练次数是10的倍数时才打印出来,“打印步数”也一样。
此处用的代码都是:
1. char buffer1[256]; 2. sprintf(buffer1,"步数为: %d\n",j); 3. ui->lineEdit_2->setText(buffer1); 用sprintf函数把整形变量转化为字符型,存在字符数组中再显示在控件上。
各种点的UI,包括起始点,轨迹,终止点,障碍物,选中点:
先上代码:
enum CellType 2. { 3. Null = 0 , Barrier = 1 , Candidate = 2, Path = 3, Selected=4, Start=5 ,End=6, Win=7 4. } type; 5. 6. void MessageControl::setCellType(CellType type) 7. { 8. 9. this->type = type; 10. if(type == MessageControl::Null) 11. { 12. 13. ui->widget->setStyleSheet(QString("background-color:%1;").arg(defaultColor.name())); // 设置背景色 14. 15. } 16. if(type == MessageControl::Barrier) 17. { 18. ui->widget->setStyleSheet(QString("background-color:%1;").arg(barrierColor.name())); // 设置背景色 19. 20. 21. } 22. if(type == MessageControl::Candidate) 23. { 24. ui->widget->setStyleSheet(QString("background-color:%1;").arg(candidateColor.name())); // 设置背景色 25. 26. } 27. if(type == MessageControl::Path) 28. { 29. 30. ui->widget->setStyleSheet(QString("background-color:%1;").arg(pathColor.name())); // 设置背景色 31. 32. } 33. if(type == MessageControl::Selected) 34. { 35. ui->widget->setStyleSheet(QString("background-color:%1;").arg(selectedColor.name())); // 设置背景色 36. 37. } 38. if(type == MessageControl::Start) 39. { 40. MessageControl::palette.setBrush(QPalette::Active, QPalette::Base, QBrush(Qt::green)); // 设置背景色 41. this->setPalette(palette); 42. } 43. if(type == MessageControl::End) 44. { 45. MessageControl::palette.setBrush(QPalette::Active, QPalette::Base, QBrush(Qt::blue)); // 设置背景色 46. this->setPalette(palette); 47. } 48. if(type == MessageControl::Win) 49. { 50. ui->widget->setStyleSheet(QString("background-color:%1;").arg(winColor.name())); // 设置背景色 51. } 52. } 思路就是为函数setCellType(CellType type)传进去一个参数,这个参数的数据类型在.h文件中定义过了,是一个元素类型,有起始点(Start)、终止点(End)、障碍物(barrier)、轨迹(Path)等,都可以用数字来表示,传到函数中之后,函数会根据type来设置对应的颜色。那么如何跟单元格选中关联起来呢,如何通过鼠标触发呢?
QT有一个与众不同的“信号和槽”机制,用connect函数可以将两个不同文件中的函数连接在一起,一个函数作为信号发出者,在发送方.h文件中定义为signal,另一个函数作为槽,接收信号,在接收方.h文件中定义为slot。
比如:
发送方: messagecontrol文件

接收方: mainwindow文件

关于QT信号与槽机制具体内容可以查看参考文献[7]。
1. //鼠标控制栅格选择 2. void MessageControl::mousePressEvent(QMouseEvent *event) //摁住鼠标事件 3. { 4. if(this->type == MessageControl::Selected) //如果已经选中了。再次点击及取消选中状态 5. { 6. this->setCellType(MessageControl::Null); 7. emit this->selectedCancelIndex(pos_y,pos_x); //给mainwindows类发送一个信号 8. } 9. else 10. { 11. this->setCellType(MessageControl::Selected); 12. emit this->selectedCellIndex(pos_y,pos_x); //给mainwindows类发送一个信 13. } 14. } 鼠标选中单元格时,会把该单元格坐标pos_x,pos_y传入信号函数,发送给mainwindow,这里emit就是发送信号的意思,mainwindow中的对应槽函数就会接收到参数,将该单元格坐标加入到已选中坐标数组中,同时给setCellType传入颜色参数,使其变色。
2.机器人路径规划算法设计
2.1 机器人行进方式
八叉树的方式行进,可以有八个运动方向:
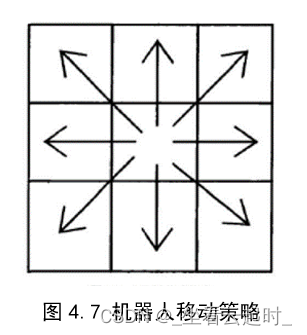
用八个常量代表八个方向:
1. const int up=1; 2. const int down =2; 3. const int Left =3; 4. const int Right=4; 5. const int leftup=5; 6. const int leftdown=6; 7. const int rightup=7; 8. const int rightdown=8; 2.2变量设置:
1. double R=0.8; //折扣因子 2. int flag=1; //用来记录机器人是否位置改变,1为改变 3. int over; //判定是否到达终点 4. double length=0.0; //打印路径长度 5. double Qtable[TABLE_COLUMN+2][TABLE_ROW+2][8]={0.0}; //存放奖励函数Q的表,每次训练更新一遍,8(方向)+1(障碍)+4(边沿)=13 6. double r[TABLE_COLUMN+2][TABLE_ROW+2]={0.0}; 7. double action(int act , int& x,int& y,int& den); 8. void initplace(int& x,int& y,int& den); 9. double get_expected_max_reward(int x,int y); 10. void actpunish(); - R:折扣因子,用来为每一次的延迟奖励打折扣;
- flag: 用来判定机器人目前位置相对于上次的位置是否发生改变,初始设置为1,代表发生改变;
- over: 判断机器人是否到终点的值;
- Qtable: Q值表,每一个单元格有八个对应的Q值,分别代表向一个方向行进的Q值是多少。比如Qtable[0][0][1]就代表在坐标(0,0)处,向上走的Q值是多少;
- r[][]: 立即奖励值,每走到一个单元格,环境都给一个立即奖励;
- Initplace:初始化,把起始点、终止点、over都初始化;
剩下几个函数前面介绍过了。
!注意:
采用 ε- 贪心策略选择动作 a,在状态 s 下执行当前动作 a,得到新状态 s' 和奖励 R。贪心系数Greedy =0.2。Q-learning本质上是贪心算法。但是如果每次都取预期奖励最高的行为去做,那么在训练过程中可能无法探索其他可能的行为,甚至会进入“局部最优”,无法完成游戏。所以,由贪心系数,使得机器人有Greedy的概率采取最优行为,也有一定概率探索新的路径。
2.3 算法步骤
(1)Action:机器人从起始点出发,有一定概率随机选择运动方向,否则向Q值最大的方向前进
(2)Reward:如果遇到边界或障碍,机器人不动,返回一个惩罚值,使该处该动作的Q值减小,下次尽量不做出该动作。
Environment:如果正常前进,根据做出的动作,由公式
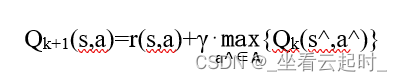
算出上一步所在格子的Q表值。
(4)超过步数限制(200步),则寻径失败。
算法流程图如下(一次训练):
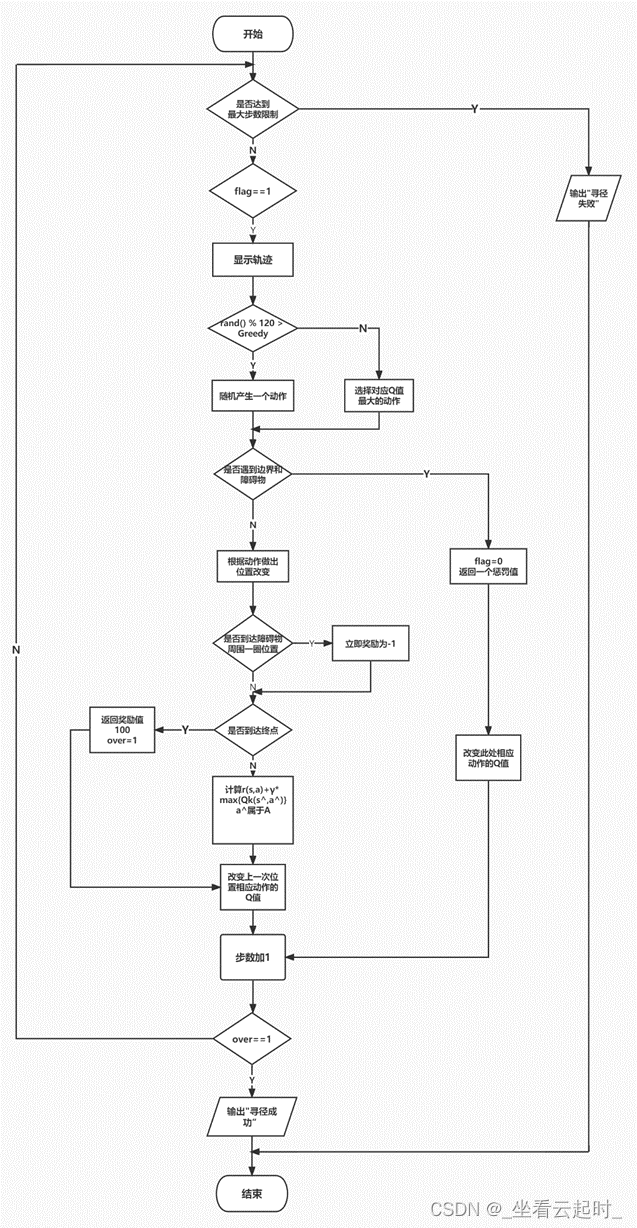
算法代码:
1. //强化学习寻径算法 2. void MainWindow::Reinforce() 3. { 4. 5. Q.actpunish(); //初始化边界惩罚值 6. int wintimes=0; //定义成功次数变量 7. int traintimes = QInputDialog::getInt(this, 8. "QInputdialog_Name", 9. "请输入要训练的次数", 10. QLineEdit::Normal, 11. 1, 12. 5000); 13. 14. for(int i=1;i<=traintimes;i++) //训练循环,traintimes为次数 15. { 16. Q.over=0; //成功与否判定变量 17. Q.initplace(start_x,start_y,Q.over); //初始化,保险 18. Q.arrived_xy.clear(); //清空暂存所在格子坐标的数组 19. Q.arrived_xy.append(QPoint(start_x,start_y)); //把起始点加入暂存所在格子坐标的数组 20. int op=0; //动作的代号 21. 22. //每次训练清空前一次的轨迹 23. for(int i=0;i<=TABLE_ROW;i++) 24. { 25. for(int j=0;j<=TABLE_COLUMN;j++) 26. { 27. MessageControl* t_MessageControl =( MessageControl*) ui->tableWidget->cellWidget(i,j); 28. t_MessageControl->setCellType(MessageControl::Null); 29. if(i==0 && j==0) 30. t_MessageControl->setCellType(MessageControl::Start); 31. if(i==TABLE_ROW && j==TABLE_COLUMN) 32. t_MessageControl->setCellType(MessageControl::End); 33. 34. } 35. } 36. 37. 38. //障碍物标记保留 39. for(auto t:Q.barrier_xy) 40. { 41. MessageControl* t_MessageControl =(MessageControl *)(ui->tableWidget->cellWidget(t.x(),t.y())); 42. t_MessageControl->setCellType(MessageControl::Barrier) 43. } 44. 45. 46. //当训练次数为10的倍数时,打印在框里 47. if(i % 10 == 0) 48. { 49. char buffer[256]; 50. sprintf(buffer,"训练次数为: %d\n",i); 51. ui->lineEdit->setText(buffer); 52. } 53. 54. //设置一个messagecontrol对象在目前所在格子 55. MessageControl* t_MessageControl =(MessageControl*) ui->tableWidget->cellWidget(Q.arrived_xy.at(0).x(),Q.arrived_xy.at(0).y()); 56. 57. for(int j = 0; j <= 100;j++) //一次训练最大不超过100步 58. { 59. 60. //走到10倍数次步数时打印步数 61. if(j % 10 == 0) 62. { 63. char buffer1[256]; 64. sprintf(buffer1,"步数为: %d\n",j); 65. ui->lineEdit_2->setText(buffer1); 66. } 67. 68. int regx=Q.arrived_xy.at(0).x(); int regy=Q.arrived_xy.at(0).y(); //提取此时坐标,后面传参要用 69. int regtwicex=regx; int regtwicey=regy; //再次暂存此时坐标,后面更新Q表要用 70. double nextmax = -100; 71. 72. if(Q.flag==1) 73. { 74. MessageControl* t_MessageControl =(MessageControl*) ui->tableWidget->cellWidget(Q.arrived_xy.at(0).x(),Q.arrived_xy.at(0).y()); 75. //如果位置改变显示轨迹 76. t_MessageControl->setCellType(MessageControl::Path); 77. 78. } 79. //有概率随机产生一个动作 80. if(rand() % 80 > Greedy) 81. { 82. op = rand() % 8 + 1; 83. } 84. 85. //如果不随机,寻找Q值最大的动作走 86. else 87. { 88. for (int m = 1; m <= 8; m++) 89. { 90. nextmax = max(nextmax + 0.0, Q.Qtable[regx][regy][m]); //遍历各个动作的Qtable值,寻找最大的那个值 91. } 92. for (int m = 1; m <= 8; m++) 93. { 94. 95. if (nextmax == Q.Qtable[regx][regy][m]) //寻找Q值最大的那个动作 96. op = m; 97. } 98. } 99. int reward = Q.action(op, regx ,regy, Q.over); //做出动作,并存下获得的奖励值 100. 101. Q.Qtable[regtwicex][regtwicey][op] += reward; 102. 103. if (Q.over == 1) 104. { 105. wintimes++; //如果成功,加1 106. 107. MessageControl* t_MessageControl =(MessageControl*) ui->tableWidget->cellWidget(Q.arrived_xy.at(0).x(),Q.arrived_xy.at(0).y()); 108. t_MessageControl->setCellType(MessageControl::Win); 109. QMessageBox MyBox(QMessageBox::NoIcon,"提示","正确,寻径成功"); 110. MyBox.exec(); 111. break; 112. } 113. 114. 115. } 116. char bufferwintimes[256]; 117. sprintf(bufferwintimes,"成功次数为: %d\n",wintimes); //展示成功次数 118. ui->lineEdit_wintimes->setText(bufferwintimes); 119. 120. if(Q.over != 1) 121. { 122. QMessageBox::critical(this,"错误","找不到路径"); 123. //控件还原 124. ui->tableWidget->setEnabled(true); 125. ui->pushButton_barrier->setEnabled(true); 126. ui->pushButton_clear->setEnabled(true); 127. ui->lineEdit->setEnabled(true); 128. ui->pushButton_find->setText("开始寻路 (Enter)"); 129. } 130. 131. 132. //打印Qtable 133. //创建文件对象,指定文件位置 134. QFile file("D:/Qt/project/robotpath/algorithmdata.txt"); 135. //对文件进行写操作 136. if(!file.open(QIODevice::WriteOnly|QIODevice::Text|QIODevice::Append)) 137. { 138. QMessageBox::information(this,"警告","请选择正确的文件!"); 139. } 140. else 141. { 142. QTextStream stream( &file ); 143. stream<<QString::number(i)<<endl; 144. if(Q.over==1) 145. stream<<"Win"<<endl<<endl; 146. else 147. stream<<"fail"<<endl<<endl; 148. for(int j=0;j<=TABLE_COLUMN;j++) { for(int i=0;i<=TABLE_ROW;i++) 149. { 150. stream<<QString::number(i)<<" "<<QString::number(j)<<":"<<" "; //打印格子坐标 151. for(int k=1;k<=8;k++) 152. { 153. stream<<QString::number(Q.Qtable[i][j][k])<<" "; //打印Qtable值 154. } 155. stream<<endl; 156. 157. } 158. } 159. stream<<endl; 160. } 161. } 162. } 163. 164. 165. void Q_learning::actpunish() 166. { 167. for(int i=0;i<=TABLE_COLUMN;i++) 168. { 169. Qtable[0][i][leftup] = S; 170. Qtable[0][i][rightup] = S; 171. Qtable[0][i][up] = S; 172. Qtable[TABLE_ROW][i][down] = S; 173. Qtable[TABLE_ROW][i][leftdown] = S; 174. Qtable[TABLE_ROW][i][rightdown] = S; 175. } 176. for(int i=0;i<=TABLE_ROW;i++) 177. { 178. 179. Qtable[i][0][Left] = S; 180. Qtable[i][0][leftup] = S; 181. Qtable[i][0][leftdown] = S; 182. Qtable[i][TABLE_COLUMN][Right] = S; 183. Qtable[i][TABLE_COLUMN][rightup] = S; 184. Qtable[i][TABLE_COLUMN][rightdown] = S; 185. } 186. Qtable[TABLE_ROW][TABLE_COLUMN][Right] = 0; 187. Qtable[TABLE_ROW][TABLE_COLUMN][down] = 0; 188. Qtable[TABLE_ROW][TABLE_COLUMN][rightdown] = 0; 189. 190. srand(time(0)); //种一个随机种子,后面选择动作要用 191. } 192. 193. 194. 195. //判断下一步选择中最大的奖励值 196. void Q_learning::initplace(int& x,int& y,int& den) //初始化机器人位置 197. { 198. x=0; 199. y=0; 200. den=0; //是否到终点,不到都为0; 201. } 202. double Q_learning::get_expected_max_reward(int x,int y) //得到最大期望Q值,用来后面传播到旧状态改变其Q值 203. { 204. double Nexstpmaxrd = -100; 205. for(int i=1;i<=8;i++) 206. { 207. Nexstpmaxrd = max(Nexstpmaxrd,Qtable[x][y][i]); 208. } 209. return Nexstpmaxrd; 210. } 211. 212. //行为函数 213. double Q_learning::action(int act , int& x,int& y,int& den) 214. { 215. //边界的惩罚 216. if((x==0 && act == Left) || (x==0 && act == leftup) || (x==0 && act == leftdown)) 217. { 218. flag=0; 219. return S; //S为遇到边界和障碍的惩罚值,会在main函数或别处全局定义,统一值为-5; 220. } 221. if((x==TABLE_ROW && act == Right ) || (x==TABLE_ROW && act == rightup) || (x==TABLE_ROW && act == rightdown)) 222. { 223. flag=0; 224. return S; 225. } 226. if((y ==0 && act == up) || (y==0 && act == leftup) || (y==0 && act == rightup)) 227. { 228. flag=0; 229. return S; 230. } 231. if((y==TABLE_COLUMN && act == down) || (y==TABLE_COLUMN && act == leftdown) || (y==TABLE_COLUMN && act == rightdown)) 232. { 233. flag=0; 234. return S; 235. } 236. //障碍物惩罚 237. if((barrier_xy.contains(QPoint(x+1,y)) && (act==Right || act == rightup || act==rightdown)) || (barrier_xy.contains(QPoint(x,y+1)) && (act==down || act == rightdown || act==leftdown)) || (barrier_xy.contains(QPoint(x,y-1)) && (act== ( up || rightup || leftup) )) || (barrier_xy.contains(QPoint(x-1,y)) && (act==Left || act == leftup || act==leftdown)) 238. || (barrier_xy.contains(QPoint(x+1,y+1)) && (act==rightdown)) || (barrier_xy.contains(QPoint(x-1,y+1)) && (act==leftdown)) || (barrier_xy.contains(QPoint(x+1,y-1)) && (act== rightup )) || (barrier_xy.contains(QPoint(x-1,y-1)) && (act==leftup ))) 239. //格子为障碍物,barrier为vector类型,在其他类中定义,里面存储了障碍物的横纵坐标(points) 240. { 241. flag=0; 242. return S; 243. } 244. 245. //其他行为,(正常行走),八叉树 246. if(act == up) 247. y--; 248. if(act == down) 249. y++; 250. if(act == Left) 251. x--; 252. if(act == Right) 253. x++; 254. if(act == leftup) 255. { 256. x--; 257. y--; 258. } 259. if(act == leftdown) 260. { 261. x--; 262. y++; 263. } 264. if(act == rightup) 265. { 266. x++; 267. y--; 268. } 269. if(act == rightdown) 270. { 271. x++; 272. y++; 273. } 274. 275. //走到障碍周围一圈的格子,立即奖励-1,因为贴近障碍,该行为不好 276. if((barrier_xy.contains(QPoint(x+1,y)))|| (barrier_xy.contains(QPoint(x,y+1)) ) || (barrier_xy.contains(QPoint(x,y-1))) || (barrier_xy.contains(QPoint(x-1,y))) 277. || (barrier_xy.contains(QPoint(x+1,y+1)) ) || (barrier_xy.contains(QPoint(x-1,y+1)) ) || (barrier_xy.contains(QPoint(x+1,y-1)) && (act== rightup )) || (barrier_xy.contains(QPoint(x-1,y-1)) )) 278. //格子为障碍物,barrier为vector类型,在其他类中定义,里面存储了障碍物的横纵坐标(points) 279. { 280. r[x][y]=-1; 281. } 282. 283. flag=1; 284. 285. arrived_xy.clear(); //清空旧位置 286. arrived_xy.append(QPoint(x,y)); //追加新位置 287. if(x == TABLE_ROW && y == TABLE_COLUMN ) //到达终点 288. { 289. den = 1; 290. return 100; //终点的奖励; 291. } 292. else if(x >= 0 && x < TABLE_ROW && y >= 0 && y < TABLE_COLUMN ) //正常走,非终点 293. { 294. double noractrew = get_expected_max_reward(x,y); 295. return r[x][y] + R * noractrew ; //计算最大奖励值 296. } 297. else 298. return 0; 299. } 五. 算法训练结果分析
主要的几个关键量:
(1)贪心因子greedy:
如果过大,随机选择一个动作的概率更高,机器人不根据Q值做决策,偏向于探索,寻找到终点的速度变慢甚至走不到终点,过小偏向于执行已知的最优策略,易陷入局部最优。这个量的设置问题在强化学习中叫作“探索与利用的平衡问题”
(2)障碍物比例
障碍物单元格数量占单元格总数量的比重,如果过高,机器人要避障,寻找到终点的速度变慢甚至走不到终点,过小算法收敛过快。
(3)惩罚值
走到边界的惩罚值与走到障碍物周围一圈的立即回报值。
(4)折扣因子
设置为0.8。
先展示寻径成功与失败的效果:


1.训练参数
决定训练次数分别设置为200,1000,2000。
每个训练集障碍物比例设置为0.2(69块),0.3(104块(约)),0.5(173块(约))
训练结束之后。绘制最短路径长度随成功次数变化的曲线图,并导出最后的Q表。
下面展示障碍物比例分别为0.2、0.3、0.5时的地图:
- 障碍物比例为0.2时:

- 障碍物比例为0.5时:

2.训练结果
数据可视化:
使用第三方库QCustomPlot,绘制折线图保存图片到本地,x轴为训练次数,折线为步数(蓝色)和行走路径长度(红色),寻径失败时步数和路径长度都设置为0。
贪心因子为15%(Greedy为85)时:
(1)训练次数为200次
- 障碍物比例为20%时
共成功到达目标点200次,最小步数为21步。
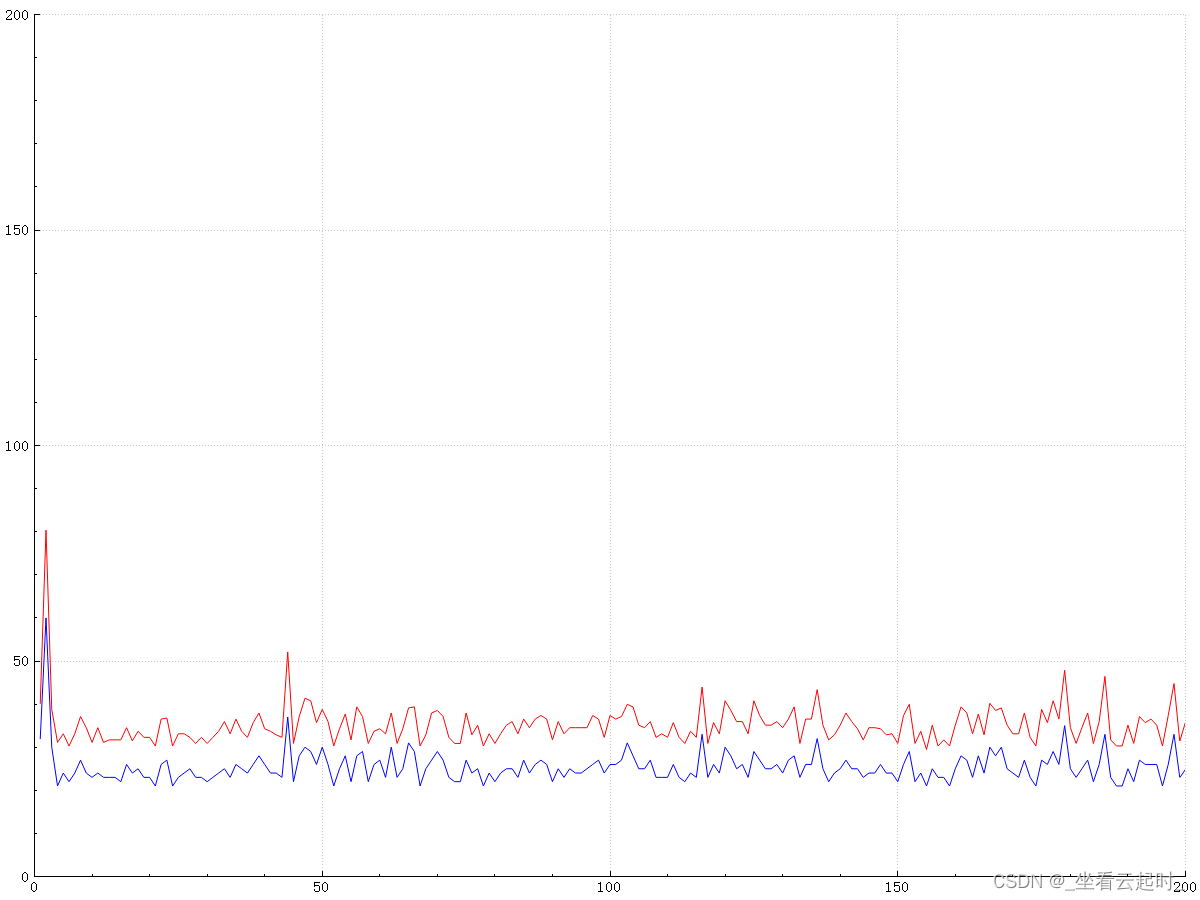
算法收敛得很快。
最终Q表值: 200 Win 35.9411 0 0: -20 0.590296 -20 0.922337 -20 -20 -20 0.922337 1 0: -20 0 0 0 -20 0 -20 1.15292 2 0: -20 1.15292 0 0 -20 0 -20 0 3 0: -20 0 0 0 -20 0 -20 0 4 0: -20 0 0 0 -20 0 -20 0 5 0: -20 0 0 0 -20 0 -20 0 6 0: -20 0 0 0 -20 0 -20 0 7 0: -20 0 0 0 -20 0 -20 0 8 0: -20 0 0 0 -20 0 -20 0 9 0: -20 0 0 0 -20 0 -20 0 10 0: -20 0 0 0 -20 0 -20 0 11 0: -20 0 0 0 -20 0 -20 0 12 0: -20 0 0 0 -20 0 -20 0 13 0: -20 0 0 0 -20 0 -20 0 14 0: -20 0 0 0 -20 0 -20 0 15 0: -20 0 0 0 -20 0 -20 0 16 0: -20 0 0 0 -20 0 -20 0 17 0: -20 0 0 0 -20 0 -20 0 18 0: -20 0 0 0 -20 0 -20 0 19 0: -20 0 0 0 -20 0 -20 0 20 0: -20 0 0 0 -20 0 -20 0 21 0: -20 0 0 0 -20 0 -20 0 22 0: -20 0 0 -20 -20 0 -20 -20 0 1: 0 0 -20 0 -20 -20 0 0.922337 1 1: 0.922337 0.922337 0.73787 0.922337 0.73787 0.590296 0.922337 1.15292 2 1: 0.472237 1.15292 0 1.44115 0 0.73787 0 1.44115 3 1: 0 0 0 0 0 0 0 1.80144 4 1: 0 0 0 0 0 0 0 2.2518 5 1: 0 0 0 0 0 0 0 0 6 1: 0 0 0 0 0 0 0 0 7 1: 0 0 0 0 0 0 0 0 8 1: 0 0 0 0 0 0 0 0 9 1: 0 0 0 0 0 0 0 0 10 1: 0 0 0 0 0 0 0 0 11 1: 0 0 0 0 0 0 0 0 12 1: 0 0 0 0 0 0 0 0 13 1: 0 0 0 0 0 0 0 0 14 1: 0 0 0 0 0 0 0 0 15 1: 0 0 0 0 0 0 0 0 16 1: 0 0 0 0 0 0 0 0 17 1: 0 0 0 0 0 0 0 0 18 1: 0 0 0 0 0 0 0 0 19 1: 0 0 0 0 0 0 0 0 20 1: 0 0 0 0 0 0 0 0 21 1: 0 0 0 0 0 0 0 0 22 1: 0 0 0 -20 0 0 -20 -20 0 2: 0 0 -20 0 -20 -20 0 0.73787 1 2: 0 0 0 0 0 0 1.15292 1.15292 2 2: 1.15292 1.15292 0.922337 1.44115 0 0.73787 1.44115 1.44115 3 2: 0 1.44115 0 0 1.15292 1.15292 0 1.80144 4 2: 0 0 0 0 0 0 0 2.2518 5 2: 0 0 0 0 0 0 0 2.81475 6 2: 0 0 0 0 0 0 0 3.51844 7 2: 0 0 0 0 0 0 0 0 8 2: 0 0 0 0 0 0 0 0 9 2: 0 0 0 0 0 0 0 0 10 2: 0 0 0 0 0 0 0 0 11 2: 0 0 0 0 0 0 0 0 12 2: 0 0 0 0 0 0 0 0 13 2: 0 0 0 0 0 0 0 0 14 2: 0 0 0 0 0 0 0 0 15 2: 0 0 0 0 0 0 0 0 16 2: 0 0 0 0 0 0 0 0 17 2: 0 0 0 0 0 0 0 0 18 2: 0 0 0 0 0 0 0 0 19 2: 0 0 0 0 0 0 0 0 20 2: 0 0 0 0 0 0 0 0 21 2: 0 0 0 0 0 0 0 0 22 2: 0 0 0 -20 0 0 -20 -20 0 3: 0 0 -20 0 -20 -20 0 0 1 3: 0 0 0 0 0 0 0 0.922337 2 3: 0 0 0 1.44115 0 0 0 1.15292 3 3: 1.44115 1.44115 1.15292 1.80144 1.15292 0.922337 0 1.80144 4 3: 0 0 1.44115 0 0 0 0 2.2518 5 3: 0 0 0 0 0 0 0 2.81475 6 3: 0 0 0 0 0 0 0 3.51844 7 3: 0 0 0 0 0 0 0 4.39805 8 3: 0 0 0 0 0 0 0 5.49756 9 3: 0 0 0 0 0 0 0 0 10 3: 0 0 0 0 0 0 0 0 11 3: 0 0 0 0 0 0 0 0 12 3: 0 0 0 0 0 0 0 0 13 3: 0 0 0 0 0 0 0 0 14 3: 0 0 0 0 0 0 0 0 15 3: 0 0 0 0 0 0 0 0 16 3: 0 0 0 0 0 0 0 0 17 3: 0 0 0 0 0 0 0 0 18 3: 0 0 0 0 0 0 0 0 19 3: 0 0 0 0 0 0 0 0 20 3: 0 0 0 0 0 0 0 0 21 3: 0 0 0 0 0 0 0 0 22 3: 0 0 0 -20 0 0 -20 -20 0 4: 0 0 -20 0 -20 -20 0 0 1 4: 0 0 0 0 0 0 0 0 2 4: 1.15292 0 0 0 0 0 0 0 3 4: 1.44115 0 0 0 0 0 0 1.80144 4 4: 1.80144 1.80144 1.44115 2.2518 1.44115 1.44115 2.2518 2.2518 5 4: 0 2.2518 1.80144 2.81475 1.80144 0 0 0 6 4: 2.81475 2.81475 2.2518 3.51844 0 2.2518 3.51844 3.51844 7 4: 0 0 0 0 2.81475 0 0 4.39805 8 4: 4.39805 4.39805 3.51844 5.49756 3.51844 3.51844 0 5.49756 9 4: 0 0 0 0 0 0 0 6.87195 10 4: 0 0 0 0 0 5.49756 0 0 11 4: 0 0 0 0 0 0 0 5.49756 12 4: 0 0 0 0 0 0 0 0 13 4: 0 0 0 0 0 0 0 0 14 4: 0 0 0 0 0 0 0 0 15 4: 0 0 0 0 0 0 0 0 16 4: 0 0 0 0 0 0 0 0 17 4: 0 0 0 0 0 0 0 0 18 4: 0 0 0 0 0 0 0 0 19 4: 0 0 0 0 0 0 0 0 20 4: 0 0 0 0 0 0 0 0 21 4: 0 0 0 0 0 0 0 0 22 4: 0 0 0 -20 0 0 -20 -20 0 5: 0 0 -20 0 -20 -20 0 0 1 5: 0 0 0 0 0 0 0 0 2 5: 0 0 0 0 0 0 0 0 3 5: 0 0 0 0 0 0 1.80144 -20 4 5: 0 0 0 0 0 0 2.2518 -20 5 5: 0 -20 1.80144 2.81475 1.80144 -20 2.81475 -20 6 5: 2.81475 0 0 0 0 0 3.51844 -20 7 5: 3.51844 -20 2.81475 4.39805 2.81475 -20 4.39805 -20 8 5: 0 0 3.51844 0 3.51844 0 0 5.49756 9 5: 5.49756 5.49756 0 6.87195 4.39805 0 4.39805 6.87195 10 5: 0 0 0 0 0 0 0 8.58993 11 5: 0 0 0 0 0 0 0 6.87195 12 5: 0 6.87195 0 0 0 0 0 0 13 5: 0 0 0 0 0 6.87195 -20 -20 14 5: 0 0 0 0 0 0 0 0 15 5: 0 0 0 0 0 0 0 0 16 5: 0 0 0 0 0 0 0 0 17 5: 0 0 0 0 0 0 0 0 18 5: 0 0 0 0 0 0 0 0 19 5: 0 0 0 0 0 0 0 0 20 5: 0 0 0 0 0 0 0 0 21 5: 0 0 0 0 0 0 0 0 22 5: 0 0 0 -20 0 0 -20 -20 0 6: 0 0 -20 0 -20 -20 0 0 1 6: 0 0 0 0 0 0 0 0 2 6: 0 0 0 0 0 0 0 0 3 6: 0 0 0 0 0 0 0 0 4 6: 0 0 0 0 0 0 0 0 5 6: 0 0 0 0 0 0 0 0 6 6: 0 0 0 0 0 0 0 0 7 6: 0 0 0 0 0 0 0 0 8 6: 0 0 -20 0 0 0 0 5.49756 9 6: 5.49756 5.49756 4.39805 0 4.39805 0 0 6.87195 10 6: 6.87195 6.87195 5.49756 8.58993 5.49756 5.49756 5.49756 8.58993 11 6: 0 0 0 0 0 6.87195 0 10.7374 12 6: 0 0 0 0 0 0 0 8.58993 13 6: 0 0 0 0 0 0 0 0 14 6: 0 0 0 0 0 0 0 0 15 6: 0 0 0 0 0 0 0 0 16 6: 0 0 0 0 0 0 0 0 17 6: 0 0 0 0 0 0 0 0 18 6: 0 0 0 0 0 0 0 0 19 6: 0 0 0 0 0 0 0 0 20 6: 0 0 0 0 0 0 0 0 21 6: 0 0 0 0 0 0 0 0 22 6: 0 0 0 -20 0 0 -20 -20 0 7: 0 0 -20 0 -20 -20 0 0 1 7: 0 0 0 0 0 0 0 0 2 7: 0 0 0 0 0 0 0 0 3 7: 0 0 0 0 0 0 0 0 4 7: 0 0 0 0 0 0 0 0 5 7: 0 0 0 0 0 0 0 0 6 7: 0 0 0 0 0 0 0 0 7 7: 0 0 0 0 0 0 0 0 8 7: 0 0 0 0 -20 0 5.49756 5.49756 9 7: 0 0 0 0 0 0 0 6.87195 10 7: 0 0 0 0 0 0 8.58993 8.58993 11 7: 8.58993 8.58993 6.87195 10.7374 6.87195 6.87195 6.87195 10.7374 12 7: 6.87195 0 0 0 0 8.58993 0 13.4218 13 7: 0 0 0 0 6.87195 10.7374 -20 -20 14 7: 0 0 0 0 0 0 0 0 15 7: 0 0 0 0 0 0 0 0 16 7: 0 0 0 0 0 0 0 0 17 7: 0 0 0 0 0 0 0 0 18 7: 0 0 0 0 0 0 0 0 19 7: 0 0 0 0 0 0 0 0 20 7: 0 0 0 0 0 0 0 0 21 7: 0 0 0 0 0 0 0 0 22 7: 0 0 0 -20 0 0 -20 -20 0 8: 0 0 -20 0 -20 -20 0 0 1 8: 0 0 0 0 0 0 0 0 2 8: 0 0 0 0 0 0 0 0 3 8: 0 0 0 0 0 0 0 0 4 8: 0 0 0 0 0 0 0 0 5 8: 0 0 0 0 0 0 0 0 6 8: 0 0 0 0 0 0 0 0 7 8: 0 0 0 0 0 0 0 0 8 8: 0 0 0 0 0 0 0 0 9 8: 0 0 0 0 4.39805 0 0 6.87195 10 8: 0 0 0 0 0 0 0 8.58993 11 8: 0 0 0 0 0 6.87195 10.7374 10.7374 12 8: 10.7374 10.7374 8.58993 13.4218 8.58993 0 8.58993 13.4218 13 8: 8.58993 0 0 0 0 0 -20 16.7772 14 8: 0 0 0 0 0 0 0 20.9715 15 8: 0 0 0 0 0 0 0 26.2144 16 8: 0 0 0 0 0 0 0 0 17 8: 0 0 0 0 0 0 0 0 18 8: 0 0 0 0 0 0 0 0 19 8: 0 0 0 0 0 0 0 0 20 8: 0 0 0 0 0 0 0 0 21 8: 0 0 0 0 0 0 0 0 22 8: 0 0 0 -20 0 0 -20 -20 0 9: 0 0 -20 0 -20 -20 0 0 1 9: 0 0 0 0 0 0 0 0 2 9: 0 0 0 0 0 0 0 0 3 9: 0 0 0 0 0 0 0 0 4 9: 0 0 0 0 0 0 0 0 5 9: 0 0 0 0 0 0 0 0 6 9: 0 0 0 0 0 0 0 0 7 9: 0 0 0 0 0 0 0 0 8 9: 0 0 0 0 0 0 0 0 9 9: 0 0 0 0 0 0 0 6.87195 10 9: 0 0 0 0 0 0 0 8.58993 11 9: 0 0 0 0 0 6.87195 10.7374 10.7374 12 9: 10.7374 10.7374 8.58993 13.4218 0 0 13.4218 13.4218 13 9: 13.4218 13.4218 10.7374 16.7772 10.7374 10.7374 16.7772 16.7772 14 9: 16.7772 16.7772 13.4218 20.9715 13.4218 13.4218 20.9715 20.9715 15 9: 0 0 0 26.2144 0 0 0 26.2144 16 9: 0 0 0 0 0 0 0 32.768 17 9: 0 0 0 0 0 0 0 40.96 18 9: 0 0 0 0 0 0 0 0 19 9: 0 0 0 0 0 0 0 0 20 9: 0 0 0 0 0 0 0 0 21 9: 0 0 0 0 0 0 0 0 22 9: 0 0 0 -20 0 0 -20 -20 0 10: 0 0 -20 0 -20 -20 0 0 1 10: 0 0 0 0 0 0 0 0 2 10: 0 0 0 0 0 0 0 0 3 10: 0 0 0 0 0 0 0 0 4 10: 0 0 0 0 0 0 0 0 5 10: 0 0 0 0 0 0 0 0 6 10: 0 0 0 0 0 0 0 0 7 10: 0 0 0 0 0 0 0 0 8 10: 0 0 0 0 0 0 0 0 9 10: 0 0 0 0 0 0 0 0 10 10: 0 0 0 0 0 0 8.58993 -20 11 10: 0 0 0 0 0 0 10.7374 -20 12 10: 0 0 0 0 0 0 13.4218 -20 13 10: 0 -20 10.7374 16.7772 10.7374 -20 16.7772 -20 14 10: 16.7772 0 13.4218 20.9715 13.4218 -20 20.9715 20.9715 15 10: 0 20.9715 0 0 16.7772 16.7772 0 26.2144 16 10: 0 26.2144 0 32.768 0 0 0 32.768 17 10: 0 0 0 40.96 26.2144 0 0 40.96 18 10: 0 0 0 0 0 0 0 51.2 19 10: 0 0 0 0 0 0 0 0 20 10: 0 0 0 0 0 0 0 0 21 10: 0 0 0 0 0 0 0 0 22 10: 0 0 0 -20 0 0 -20 -20 0 11: 0 0 -20 0 -20 -20 0 0 1 11: 0 0 0 0 0 0 0 0 2 11: 0 0 0 0 0 0 0 0 3 11: 0 0 0 0 0 0 0 0 4 11: 0 0 0 0 0 0 0 0 5 11: 0 0 0 0 0 0 0 0 6 11: 0 0 0 0 0 0 0 0 7 11: 0 0 0 0 0 0 0 0 8 11: 0 0 0 0 0 0 0 0 9 11: 0 0 0 0 0 0 0 0 10 11: 0 0 0 0 0 0 0 0 11 11: 0 0 0 0 0 0 0 0 12 11: 0 0 0 0 0 0 0 0 13 11: 0 0 0 0 0 0 0 0 14 11: 16.7772 0 0 0 0 0 0 20.9715 15 11: 20.9715 20.9715 0 0 16.7772 16.7772 26.2144 26.2144 16 11: 0 26.2144 0 32.768 20.9715 0 32.768 32.768 17 11: 32.768 32.768 26.2144 40.96 26.2144 26.2144 0 40.96 18 11: 40.96 0 32.768 0 32.768 32.768 0 51.2 19 11: 0 0 0 0 0 0 0 64 20 11: 0 0 0 0 0 0 0 0 21 11: 0 0 0 0 0 0 0 0 22 11: 0 0 0 -20 0 0 -20 -20 0 12: 0 0 -20 0 -20 -20 0 0 1 12: 0 0 0 0 0 0 0 0 2 12: 0 0 0 0 0 0 0 0 3 12: 0 0 0 0 0 0 0 0 4 12: 0 0 0 0 0 0 0 0 5 12: 0 0 0 0 0 0 0 0 6 12: 0 0 0 0 0 0 0 0 7 12: 0 0 0 0 0 0 0 0 8 12: 0 0 0 0 0 0 0 0 9 12: 0 0 0 0 0 0 0 0 10 12: 0 0 0 0 0 0 0 0 11 12: 0 0 0 0 0 0 0 0 12 12: 0 0 0 0 0 0 0 0 13 12: 0 0 0 0 0 0 0 0 14 12: 0 0 0 0 0 0 20.9715 -20 15 12: 0 0 0 0 0 0 26.2144 -20 16 12: 26.2144 -20 20.9715 0 20.9715 -20 32.768 -20 17 12: 32.768 32.768 0 40.96 0 0 40.96 0 18 12: 40.96 0 32.768 51.2 32.768 0 0 51.2 19 12: 0 51.2 0 64 40.96 0 0 64 20 12: 0 0 51.2 0 0 51.2 0 80 21 12: 0 0 0 0 0 0 0 0 22 12: 0 0 0 -20 0 80 -20 -20 0 13: 0 0 -20 0 -20 -20 0 0 1 13: 0 0 0 0 0 0 0 0 2 13: 0 0 0 0 0 0 0 0 3 13: 0 0 0 0 0 0 0 0 4 13: 0 0 0 0 0 0 0 0 5 13: 0 0 0 0 0 0 0 0 6 13: 0 0 0 0 0 0 0 0 7 13: 0 0 0 0 0 0 0 0 8 13: 0 0 0 0 0 0 0 0 9 13: 0 0 0 0 0 0 0 0 10 13: 0 0 0 0 0 0 0 0 11 13: 0 0 0 0 0 0 0 0 12 13: 0 0 0 0 0 0 0 0 13 13: 0 0 0 0 0 0 0 0 14 13: 0 0 0 0 0 0 0 0 15 13: 0 0 0 0 0 0 0 0 16 13: 0 0 0 0 0 0 0 0 17 13: 0 0 0 0 0 0 40.96 -20 18 13: 0 0 0 0 0 -20 0 0 19 13: 51.2 0 0 64 40.96 0 0 0 20 13: 64 0 51.2 80 51.2 0 0 0 21 13: 0 0 64 0 64 0 0 100 22 13: 0 100 0 -20 0 0 -20 -20 0 14: 0 -20 -20 0 -20 -20 0 -20 1 14: 0 -20 0 0 0 -20 0 -20 2 14: 0 -20 0 0 0 -20 0 -20 3 14: 0 -20 0 0 0 -20 0 -20 4 14: 0 -20 0 0 0 -20 0 -20 5 14: 0 -20 0 0 0 -20 0 -20 6 14: 0 -20 0 0 0 -20 0 -20 7 14: 0 -20 0 0 0 -20 0 -20 8 14: 0 -20 0 0 0 -20 0 -20 9 14: 0 -20 0 0 0 -20 0 -20 10 14: 0 -20 0 0 0 -20 0 -20 11 14: 0 -20 0 0 0 -20 0 -20 12 14: 0 -20 0 0 0 -20 0 -20 13 14: 0 -20 0 0 0 -20 0 -20 14 14: 0 -20 0 0 0 -20 0 -20 15 14: 0 -20 0 0 0 -20 0 -20 16 14: 0 -20 0 0 0 -20 0 -20 17 14: 0 -20 0 0 0 -20 0 -20 18 14: 0 -20 0 0 0 -20 51.2 -20 19 14: 0 -20 0 0 0 -20 64 -20 20 14: 0 -20 0 0 0 -20 80 -20 21 14: 0 -20 0 0 0 -20 0 -20 22 14: 0 0 0 0 0 -20 -20 0 如果将贪心因子设置为40%(Geedy为60) :
训练200次时:
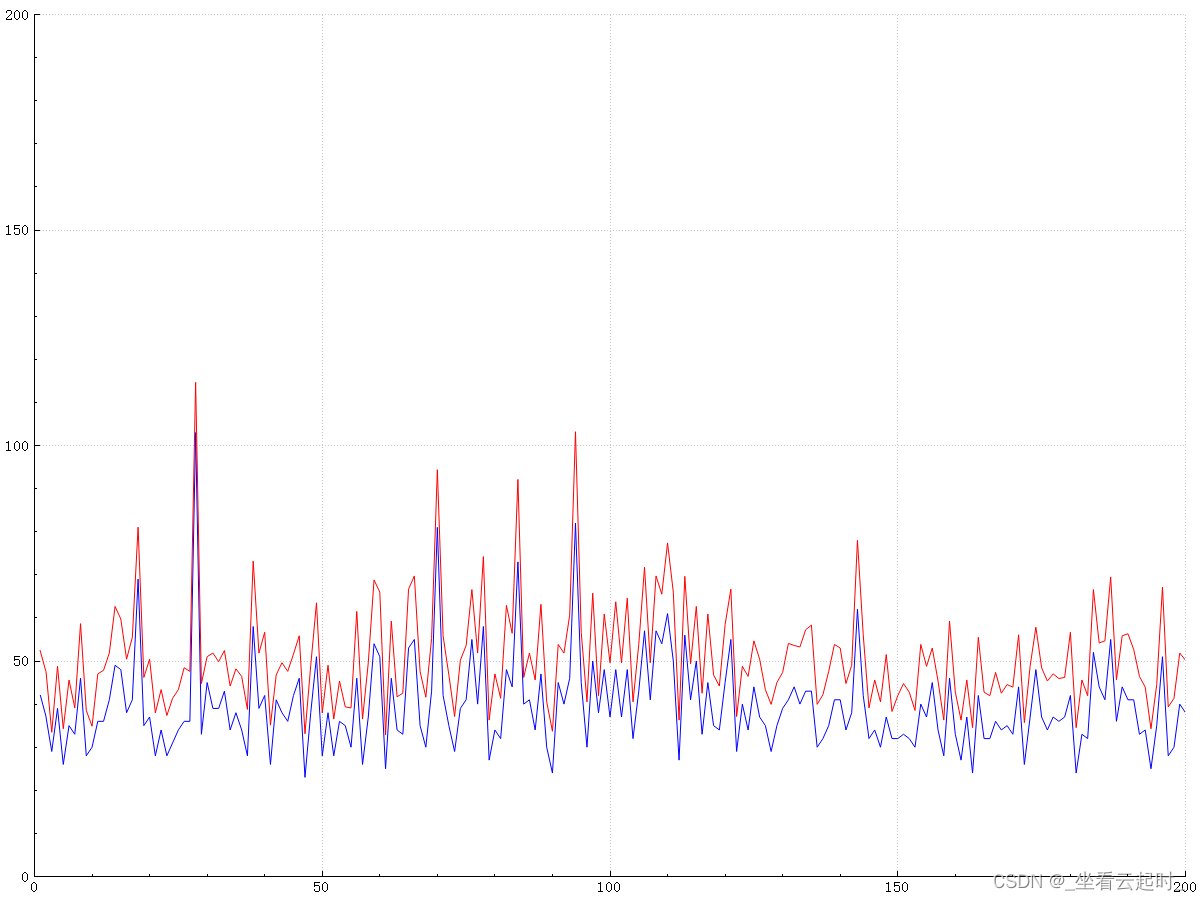
可以发现收敛性不如15%时。
- 障碍物比例为50%时
共成功到达目标点198次,最小步数为23
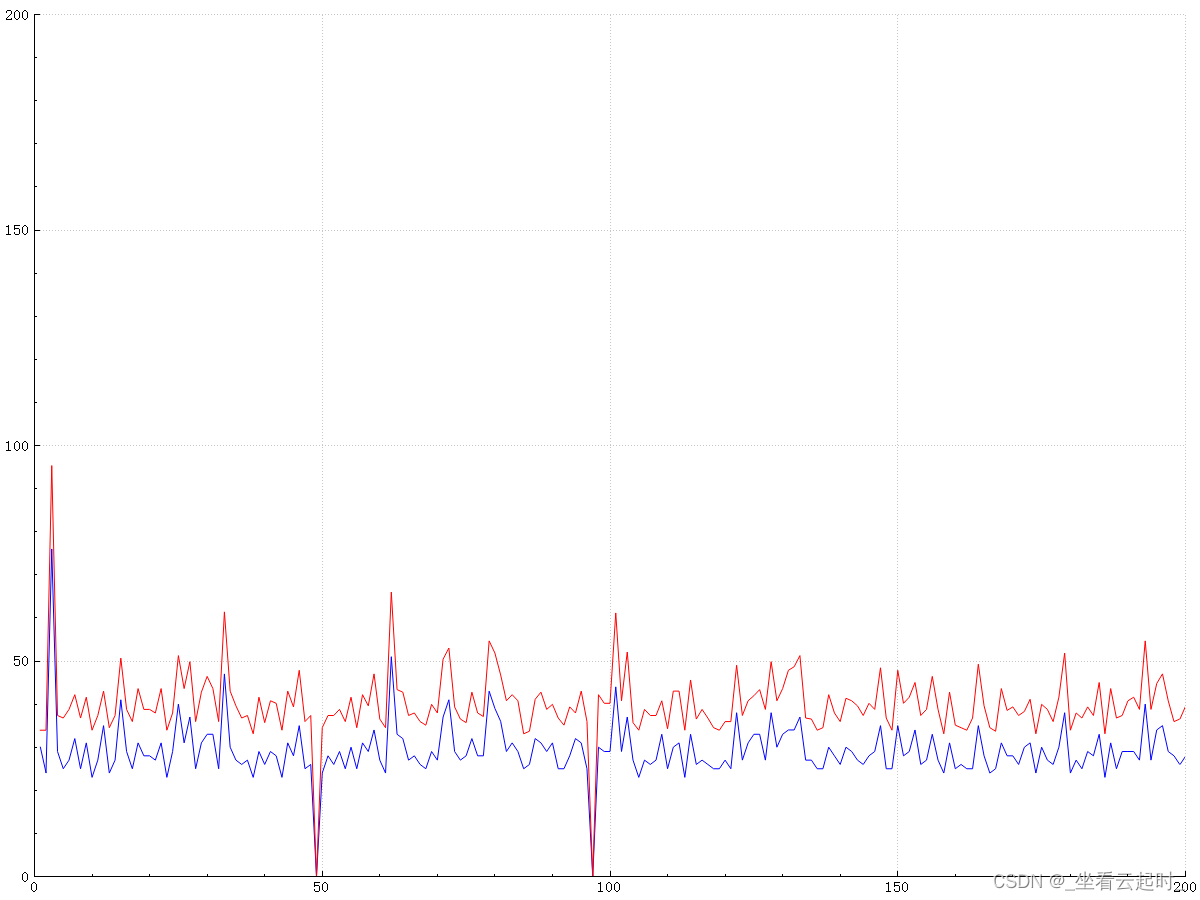
(2)训练次数为500次
贪心因子为15%:
- 障碍物比例为20%时
共成功到达目标点493次,最小步数21步。
可观察出这样几个现象:
(1)相同训练次数的情况下,随着障碍物比例增加,成功率会有所减少。
(2)贪心因子越大,算法收敛越慢
六.实践过程、体会与反思
本次是想借着这个课题多学一些东西,包括算法设计技能和代码开发技能,选题结束后,先是用大概一个晚上的时间了解了机器学习的大概知识,在监督学习、无监督学习、强化学习中选择了通过与环境交互来修改自身策略的强化学习算法,阅读了讲解马尔可夫决策过程、Q-learning算法等知识的文献,最后决定选择Q-learning算法来做机器人路径规划,借此来入门人工智能,对创造出的智能体通过探索来自我学习出一套策略的这种思想叹为观止。
然后阅读了一些相关博客,了解他人在开发中如何将Q-learning算法代码话,情景化,应用到具体的路线规划中,因为时间不是很充裕,之前我又没有学习过python与matlab,但我知道这两种语言在人工智能开发中应用最广,且效率很高,但由于现实条件,我只能选择熟悉的C++语言来开发算法的应用框架,通过资料检索,我选择了两篇博客作为主要参考文献,一篇指导开发情景,一篇指导开发算法,应用Qt Creator作为开发工具,开发情景花费了很多时间,大概有四五个整天,因为我基本是从0开始上手QT,中间边开发边遇错,边搜索边学习才把情景开发齐全,后面大概又四五天不断地发现错误并改错,最后在2022年12月16日开始训练算法,开发过程很烧脑,但通过这一个小项目让我对QT开发有了初步了解,增强了代码改错能力,信息搜集能力,也算是有所收获。
初次训练结果不好,次数少的时候,由于Q-learning算法搜索效率低,成功的次数很少,但是训练次数多了的时候,却又有别的问题,因为我是把每次训练的结果都写入两个txt文件,当我打开文件查看结果时,属实吃了一惊,一些奇奇怪怪的数字让我很困惑是从何而来,但是我又想不出是什么问题,Q表的更新为什么会在若干次训练之后变的非常混乱,是算法的问题,还是电脑的问题,我也不得而知,把数据放到excel生成折线图后会发现成功寻径时的步数和路径长度都是震荡的,而不是呈现出下降后收敛成一条直线的状态(中国矿业大学数学学院的一篇硕士研究生论文(文献[8])中的仿真结果图像就是这样)。因为寻找错误->搜索资料->修改算法->参数调优->训练结果->撰写报告等等一些工作还会耗费大量的时间,权衡利弊,我决定先停在这里,后续时间充沛时,或者开学遇到老师和同学时再做以后的更改。
续:
一年后我再次打开这个项目,对代码重新进行梳理,感谢评论区一位朋友的提醒,在更新Q值得时候我在reward后面写的是+=,实际上按照强化学习理论,应该是=,改正后算法果然很好的收敛。
七.算法改进和研究展望
1.基于Q-learning算法改进研究现状
很多研究将启发式算法与强化学习算法相结合来改进算法,利用启发式算法的一些优点特性来弥补Q-learning算法的不足,文献[8]—[10]就是相关的例子。
文献[8]针对Q-learning算法前期搜索效率低,规划路线慢甚至找不到目的地的缺点进行改进,作者观察到Q值表与蚁群算法的信息素矩阵结构相同,意义相近,因此作为两种算法的结合点,对基本蚁群算法进行改进后融合入Q-learning算法,得到了很好的效果。 文献[9] 提出了一种基于萤火虫算法的Q-learning算法,尝试在加快Q-learning算法收敛速度的同时,避免算法陷入局部最优。首先利用萤火虫算法寻优能力强的特点初始化Q值;其次在Q-learning算法的动作选择过程中,将迭代信息嵌入到选择策略中,设计了混合选择策略,令算法可以动态选择贪婪搜索策略和根据Q值搜索策略,避免算法陷入到局部最优;文献[10]中Liw 等针对三维无人机路径规划问题,提出了基于A*和Q-learning算法的混合算法,混合算法中设计了自适应探索因子,以提高改进算法的收敛速度;文献[11]针对Q-learning算法收敛速度慢,学习时间长的问题,提出了一种基于具有先验知识的改进 Q-learning 移动机器人路径规划算法。该路径规划算法在原来标准 Q-learning 算法的基础上增加了一层深度学习层、在算法初始化的过程中加入了关于环境的先验知识作为启发信息并且根据不同的状态在构建的标量场中的位置获得不同的奖赏值来使得奖赏值具有导向性,解决了算法学习初始阶段的无目的性,使得算法在学习过程中具有导向性,提高了算法的学习效率以及算法的收敛速度。文献[12]针对移动机器人采用强化学习方法进行路径规划时存在的学习效率低及收敛速度慢等问题,提出一种改进的Q-learning 算法。首先提出动态动作集策略,根据机器人当前点与终点的位置来选择其动作 集;然后在算法中加入启发式奖惩函数,使得机器人采取不同的动作收获不同的奖励。由此来改进算法, 进而提高算法的学习效率,加快算法收敛。文献[13] 结合Q-learning算法和 Sarsa算法的优点,设计了基于前馈神经网络的Q-learning算法,并将其应用到无人机器人的路径规划问题中;
目前一种将深度学习的感知能力和强化学习的决策能力相结合的算法——深度强化学习,在机器人路径规划中发挥了重要作用,相关研究也层出不穷,文献[14] 将前沿的深度强化学习算法应用于移动机器人路径规划问题中,使移动机器人通过强化学习算法在未知环境下进行探索与学习,并训练其决策能力,最终实现连续动作空间下的路径规划与避障。文献[15] 将全局路径规划算法和局部路径规划算法进行结合,研究基于深度强化学习的路径规划算法,在此基础上进一步研究多机器人编队控制算法,并在基于ROS平台的轮式机器人上进行实验验证。根据机器人半径对原始地图的障碍物栅格进行扩张,避免规划出的路径紧贴障碍;在评价函数中使用路径长度和转弯角度作为代价值,并使用时间统一计算,以找出一条转折点较少的路径;在找出路径之后通过平滑算法进一步优化,得到更有利于机器人控制的路径。而且研究了基于深度强化学习的局部路径规划算法,提出了改进深度确定性策略梯度(DDPG)算法。
2.本文算法的后期改进展望
文献[16]给我较大启发,该文献剖析了强化学习算法在路径规划中的不足以及改进的一些可行方向。在该开始的学习过程中,智能体(机器人)对环境一无所知,此时如果状态空间很大,奖励值又很稀疏,很多奖励值都初始化为0,那么智能体就会用大量时间作无意义的搜索,因为找到有意义的奖赏值概率很小,这就是强化学习算法收敛非常慢的主要原因。
该文章提出了一个“启发式策略选择”的概念,就是在强化学习中融入人的先验知识或者过程知识来设计和优化启发式奖赏函数,与原有的根据Q值表进行动作选择的策略相融合,来使智能体更快达到最优。
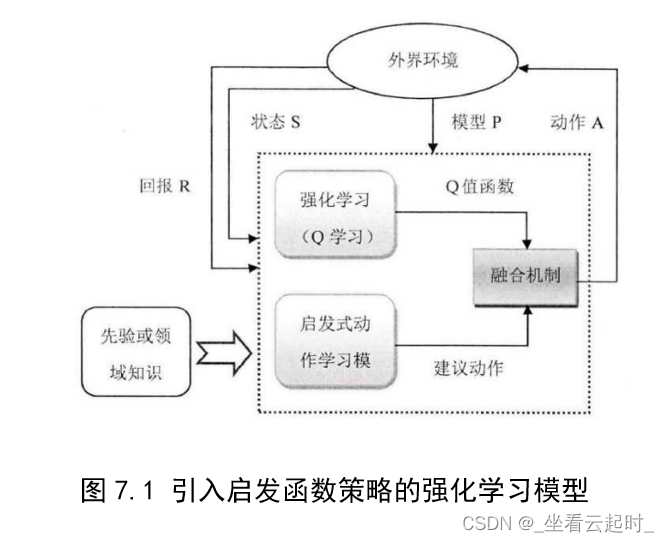
而且做出的动作选择是要有概率性的:
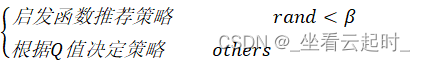
当生成的随机数小于β时,采用我们的启发式策略推荐一个动作,帮助智能体更好的探索,如果随机数大于等于β,就让智能体自己根据Q值做出动作,让β随着迭代次数逐渐减小,因为Q表逐渐成熟,到后期就不要我们的启发式推荐了。这就相当于大人在儿童年幼时帮助其走路,指引其决策,随着儿童自己的学习,知识体系日趋成熟,大人也就可以减小干预。
我打算后期如果有机会改进时,采用这种策略,启发函数我打算就设置为:做出决策后,会导致下一步格子距离目标点的直线距离最短所对应的那个动作,只是一个构想,后期还需要测试实践。
个人想法:
可以让贪心因子随着训练次数得增加而衰减,可能会有更好的效果,另外可以用深度强化学习做该项目,减小Qtable带来的开销,效果会更好。
ID:_坐看云起时_ _坐看云起时_的博客_CSDN博客-操作系统,计算机系统与硬件,OJ领域博主
程序、代码存放在:
链接: https://pan.baidu.com/s/1cHjlQejszNAs9hqTub4Xzw?pwd=ct7y
提取码: ct7y
参考文献:
[1]王鹤静,王丽娜.机器人路径规划算法综述[J/OL].桂林理工大学学
报:1-15[2022-12-14].http://kns.cnki.net/kcms/detail/45.1375.N.20221213.1104.001.html
[2]基于可视图法(VG)的路径规划算法简述_慕羽★的博客-CSDN博客_vg算法
[3]向征,赵歆波,曹师好,张宝尚.基于遗传算法的铁路列车图像配准研究[J].中国体视学与图像分析,2021,26(03):253-260.DOI:10.13505/j.1007-1482.2021.26.03.006.
[4] 《人工智能导论》(第三版),丁世飞著
[5] 人工智能学习之机器人路径规划优化_榕林子的博客-CSDN博客_人工智能路径规划
[6] 基于Q-learning的无人机三维路径规划(含完整C++代码)_~在下小吴的博客-CSDN博客_无人机三维路径规划
[7] qt中connect函数探究_jKingle的博客-CSDN博客
[8] 柯逸. 基于蚁群Q-learning算法的移动机器人路径规划[D].中国矿业大学,2022.DOI:10.27623/d.cnki.gzkyu.2022.000545.
[9] 王付宇,张康,谢昊轩,陈梦凯.基于改进Q-learning算法的移动机器人路径优化[J].系统工程,2022,40(04):100-109.
[10] D. Li, W. Yin, W. E. Wong, M. Jian and M. Chau, "Quality-Oriented Hybrid Path Planning Based on A* and Q-Learning for Unmanned Aerial Vehicle," in IEEE Access, vol. 10, pp. 7664-7674, 2022, doi: 10.1109/ACCESS.2021.3139534.
[11] 王慧,秦广义,夏鹏,杨春梅,王刚.基于改进强化学习算法的移动机器人路径规划研究[J].计算机应用与软件,2022,39(07):269-274.
[12] 潘国倩,周新志.基于启发式强化学习的移动机器人路径规划算法研究[J].现代计算机,2022,28(10):57-61.
[13] Wang Y H , Li T , Lin C J . Backward Q-learning: The combination of Sarsa algorithm and Q-learning[J]. Engineering Applications of Artificial Intelligence, 2013, 26(9):2184-2193.
[14] 吴亚琦. 基于深度强化学习的移动机器人自主路径规划研究[D].华东交通大学,2021.DOI:10.27147/d.cnki.ghdju.2021.000229.
[15] 周盛世. 基于深度强化学习的机器人路径规划算法研究[D].南京理工大学,2021.DOI:10.27241/d.cnki.gnjgu.2021.002288.
[16]马朋委. Q_learning强化学习算法的改进及应用研究[D].安徽理工大学,2016.
