目录
前言
在前面学习过二叉树的时候我们就已经接触到深度优先搜索和广度优先搜索,二叉树的前序遍历和后序遍历都属于深度优先遍历的一种,但是对于二叉树这种有规律的数据结很容易理解,但是如果是对于图这种没有规律的数据结构又该如何去实现深度优先和广度优先遍历呢?下面就一起来看看吧!
深度优先遍历(DFS)
1.基本概念
深度优先搜索是用来遍历或搜索树和图数据结构的算法,它是可以从任意跟节点开始,选择一条路径走到底,并通过回溯来访问所有节点的算法。简单来说就是通过选择一条道路走到无路可走的时候回退到上一个岔路口,并标记这条路已走过,选择另外一条道路继续走,直到走遍每一条路。(一句话概括:一路走到黑,黑了就回头)
2.算法思想
Dfs思修基于递归思想,通过递归的形式来缩小问题规模,把一件事分割成若干个相同的小事,逐步完成。
深度优先搜索的步骤分为 1.递归下去 2.回溯上来。顾名思义,深度优先,则是以深度为准则,先一条路走到底,直到达到目标。这里称之为递归下去。
否则既没有达到目标又无路可走了,那么则退回到上一步的状态,走其他路。这便是回溯上来。
3.二叉树的深度优先遍历(例子)
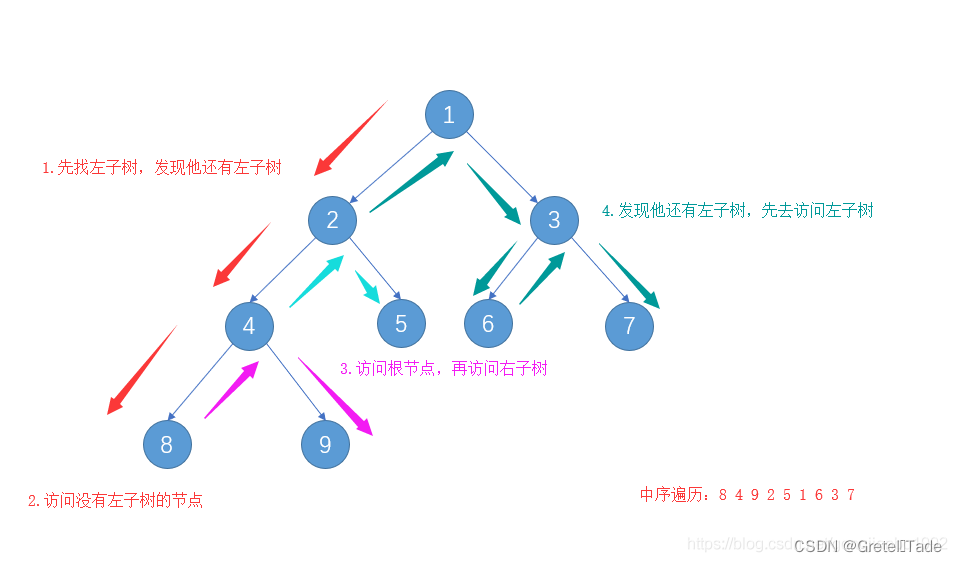
为了大家更好的了解深度优先遍历的算法,我下面举一个二叉树深度优先遍历的例子,如下图所示的一个二叉树,对其进行前序遍历(深度优先遍历)
结果为: A B D H I E J C F K G

前序遍历就是从根结点出发,一直向左子节点走,直到左子节点不存在然后返回到上一个节点走这个节点的右子节点,然后一直往右子节点走,同样的也是走不通为止就返回。很显然这种一路走到黑,黑了就回头的方式,就是深度优先遍历的过程。
图的深度优先遍历
对于二叉树的深度优先遍历大家都很好理解,但是如果对于图的话,那怎么去进行深度优先遍历呢?

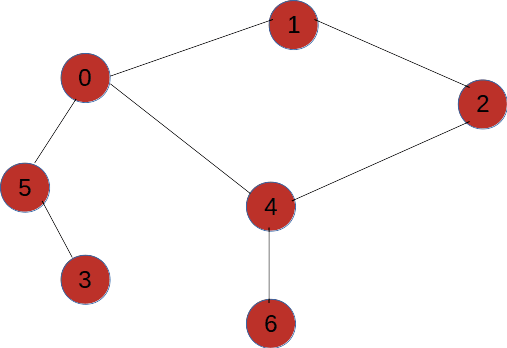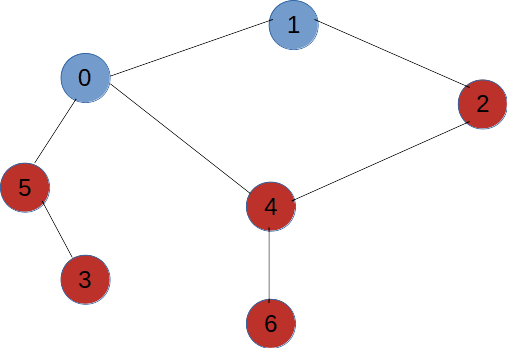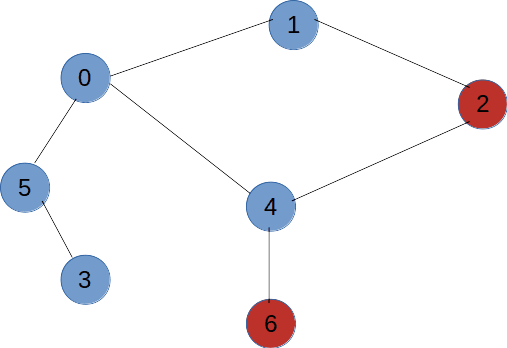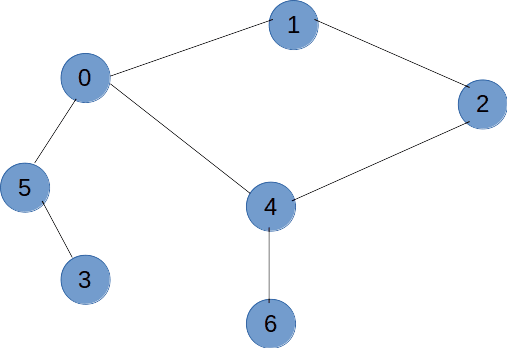
如图所示,拿到这么一个图我们从V1开始对其进行深度优先遍历,那么每一次遇到分叉点走不同的路径遍历到的结果是不一样的,所以对于一个图的深度优先变量结果可以为多种。
深度优先遍历算法步骤
- 访问初始结点v,并标记结点v为已访问。
- 查找结点v的第一个邻接结点w。
- 若w存在,则继续执行4,如果w不存在,则回到第1步,将从v的下一个结点继续。
- 若w未被访问,对w进行深度优先遍历递归(即把w当做另一个v,然后进行步骤123)
- 查找结点v的w邻接结点的下一个邻接结点,转到步骤3。
在此之前我们学习了图的两种储存方式,分别是邻接矩阵和邻接表,那么这两种存储方式进行深度优先遍历结果会有什么不同呢?我们接着看。
1.图(graph)邻接矩阵的深度优先遍历
思路分析
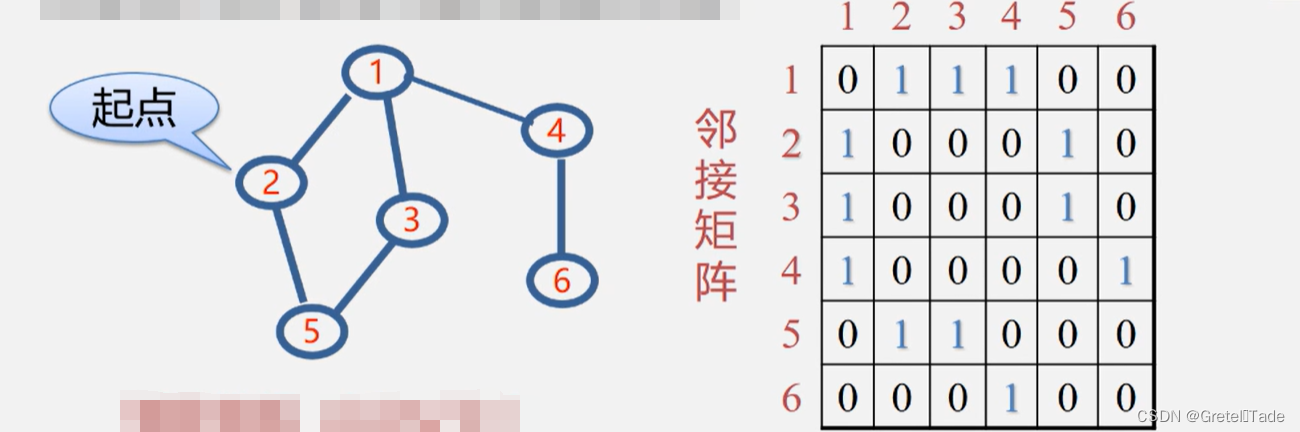
如上图所示,从2位置开始进行深度优先遍历,由于图可能是具有环形结构的,为了避免进入到环内的死循环,这里我们需要用到一个辅助数组visited来标记某一个顶点是否遍历过,如果遍历过的话,那么就不走这个方向,如果全部的方向都被标记遍历过,那就返回到上一个位置,换一个方向去遍历。(递归算法)
对于visited数组,初始化为0,表示未访问过,如果访问了的话那么就设置为1
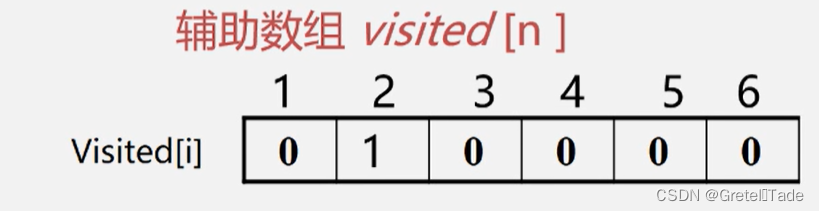
最后整个图遍历完成之后,visited数组里面的数组全都为1 ,也就是说这个图已经变量完成了
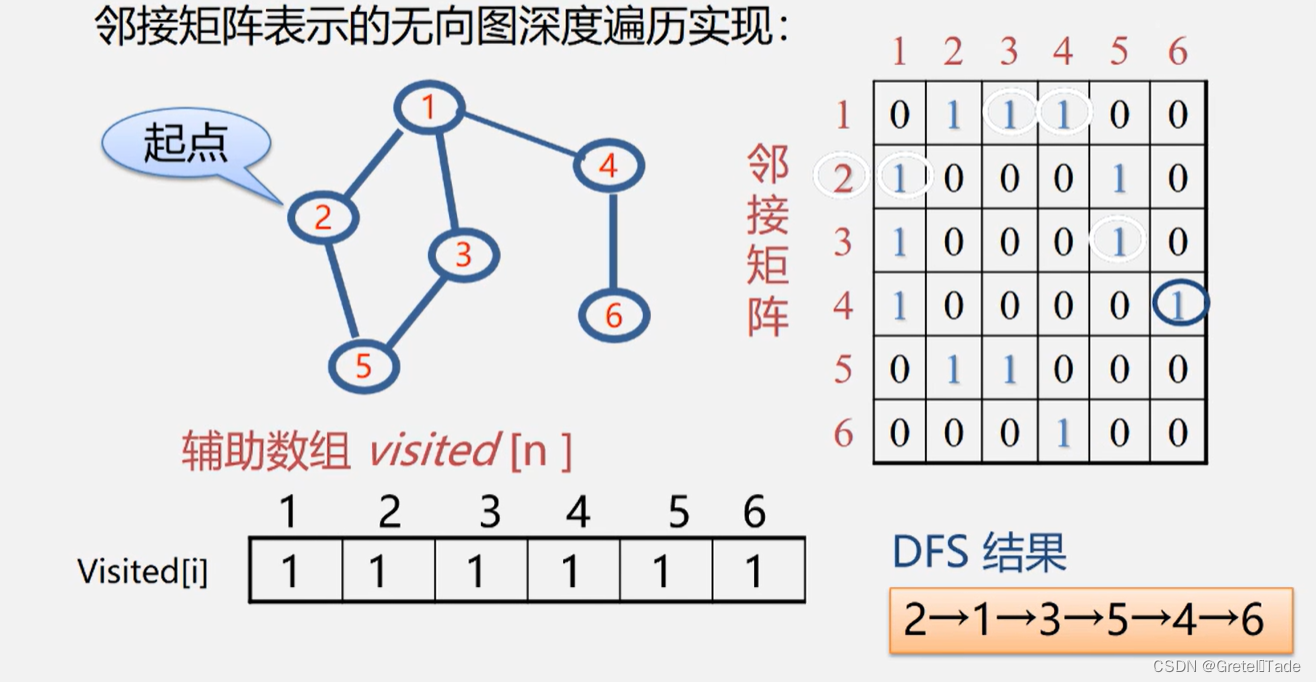
代码实现
#include<stdio.h> #include<stdlib.h> #include<string.h> #define Maxint 32767 #define Maxnum 100//最大顶点数 //数据类型 typedef struct d { char id[10]; //…… } ElemType; //图的邻接数组 typedef struct graph { ElemType vexs[Maxnum];//图数据 int matrix[Maxnum][Maxnum];//二维数组矩阵 int vexnum;//点数 int arcnum;//边数 }Graph; //节点id查找下标 int Locate_vex(Graph G, char* id) { for (int i = 0; i < G.vexnum; i++) if (strcmp(G.vexs[i].id,id)==0) return i; return -1; } //构造邻接矩阵(无向图,对称矩阵)(有向图)赋权图 void Create_graph(Graph* G) { printf("请输入顶点个数和边的个数:\n"); scanf("%d %d", &G->vexnum, &G->arcnum);//输入点数边数 printf("请输入顶点数据:\n"); for (int i = 0; i < G->vexnum; i++) { scanf("%s", G->vexs[i].id); } for (int x = 0; x < G->vexnum; x++) { for (int y = 0; y < G->vexnum; y++) { if (x == y) G->matrix[x][y] = 0;//对角线初始化为0 else G->matrix[x][y] = Maxint;//其他初始化为Maxint } } printf("请输入边相关数据:\n"); for (int k = 0; k < G->arcnum; k++) { char a[10], b[10]; int w; scanf("%s %s %d", a, b, &w); //a->b int i = Locate_vex(*G, a); int j = Locate_vex(*G, b); //矩阵赋值 G->matrix[i][j] = w; G->matrix[j][i] = w;//删掉这个,表示有向图 } } //输出矩阵 void print_matrix(Graph G) { printf("矩阵为:\n"); for (int i = 0; i < G.arcnum; i++) { for (int j = 0; j < G.arcnum; j++) printf("%-5d ", G.matrix[i][j]); printf("\n"); } printf("图的顶点个数和边数:%d,%d\n", G.vexnum, G.arcnum); } //访问输出 void visit(Graph G,int loca) { printf("%s ", G.vexs[loca].id); } //深度优先遍历DFS void DFS(Graph G, char* begin,int* visited) { int loca = Locate_vex(G, begin); visit(G, loca); visited[loca] = 1;//访问完后,visited对应的下标标记为1 for (int i = 0; i < G.vexnum; i++) {//当前顶点对其他顶点进行遍历,如果有通路就执行访问操作 if (G.matrix[loca][i] != 0&& G.matrix[loca][i]!=Maxint ) if(!visited[i])//如果visited为0的话(下一个顶点未访问过),那么就进入到下一个顶点继续访问 DFS(G, G.vexs[i].id , visited); } return; } int main() { Graph G; Create_graph(&G); print_matrix(G); int* visited = (int*)malloc(sizeof(int) * G.vexnum); memset(visited, 0, sizeof(int)*G.vexnum);//初始化为0 printf("DFS:\n"); DFS(G, "B" , visited); } 输出结果: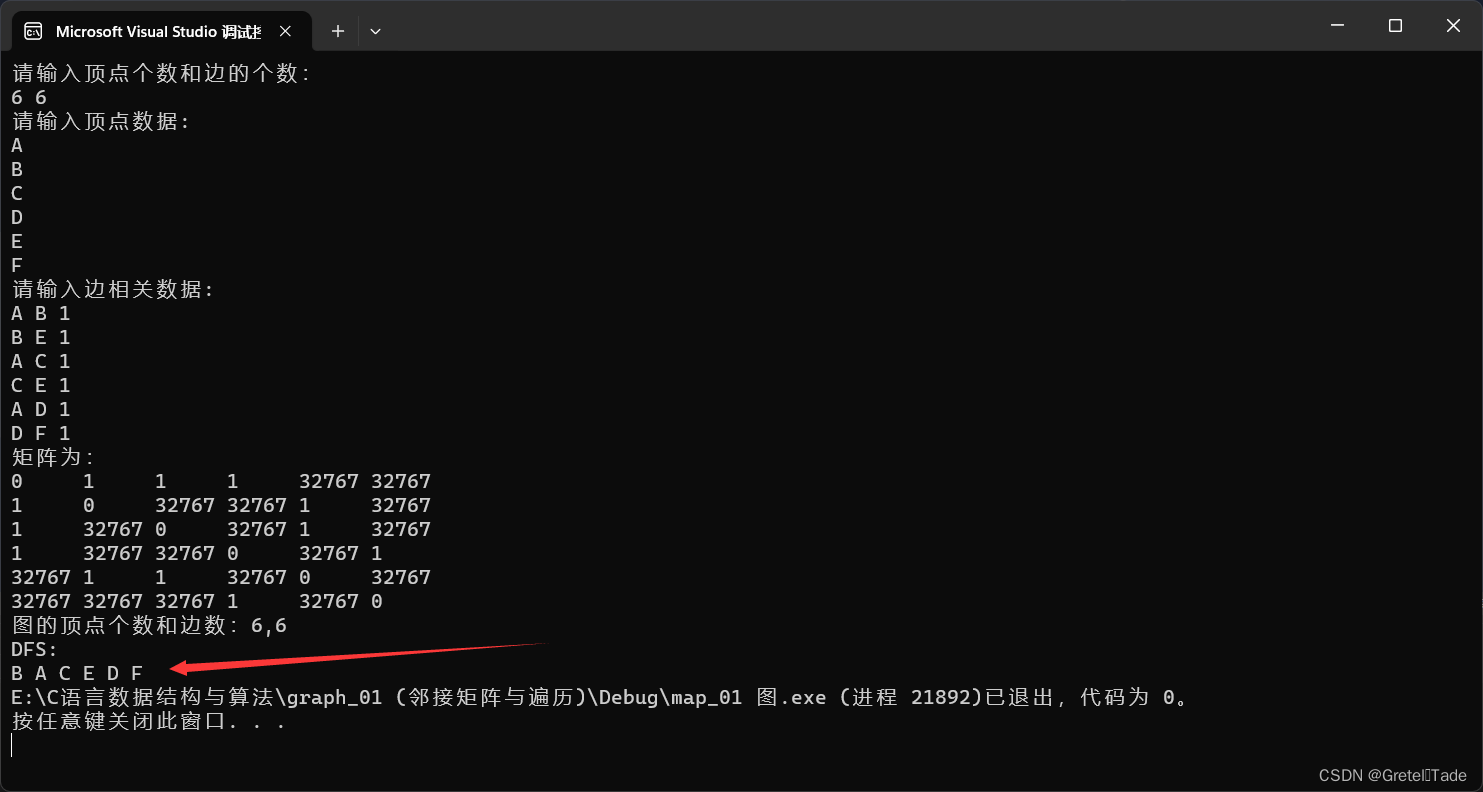
2.图(graph)邻接表的深度优先遍历
思路分析
前面我们学习过了邻接表是由两种节点组成的,分别是头结点和边节点,头结点是用来储存数据的,而变节点是用来储存于当前节点有通路的节点的引索。如图所示

对于邻接表的话,那怎么去书写代码呢?同样的我们还是需要一个visited数组来标记已经访问过的节点,然后对下一个节点进行判断是否访问过,如果没有访问过那么就进入到下一个节点的递归,如果访问过那就换一个方向继续访问,如果都访问过,那就返回到上一个节点的位置重复以上的操作。下面我提供两种代码的书写方式,分别是递归和非递归来去实现深度优先遍历。
代码实现
创建图代码(邻接表):
#include<stdio.h> #include<string.h> //数据结构体 typedef struct datatype { char id[10];//字符串编号 //……………… }ElemType; //边节点存储结构 typedef struct arcnode { int index;//指向顶点的位置 int weight;//权 struct arcnode* nextarc;//指向下一个边节点 }Anode; //顶点结点存储结构 typedef struct vexnode { ElemType data; Anode* firstarc; }Vhead; //图结构 typedef struct { Vhead* vertices; int vexnum; int arcnum; }Graph; //顶点id查找下标 int Locate_vex(Graph G, char* id) { for (int i = 0; i < G.vexnum; i++) if (strcmp(G.vertices[i].data.id,id)==0) return i; return -1; } //创建头节点 void Create_vexhead(Graph *G,int n) { G->vertices = (Vhead*)malloc(sizeof(Vhead) *n); if (!G->vertices) { printf("ERROR\n"); exit(-1); } else { for (int i = 0; i < n ; i++) { scanf("%s", G->vertices[i].data.id); G->vertices[i].firstarc = NULL; } } } //创建一个边节点 Anode* Create_arcnode(int loca, int w) { Anode* arc = (Anode*)malloc(sizeof(Anode)); if (!arc) { printf("ERROR\n"); exit(-1); } arc->index = loca; arc->nextarc = NULL; arc->weight = w; return arc; } //创建邻接表(无向图)(有向图) void Create_graph(Graph* G) { printf("输入顶点数和边数:\n"); scanf("%d %d", &G->vexnum, &G->arcnum); printf("输入顶点数据:\n"); Create_vexhead(G, G->vexnum); printf("输入边数据:\n"); for (int k = 0; k <G->arcnum; k++) { ElemType a, b; int w; scanf("%s%s%d", a.id, b.id, &w); int i = Locate_vex(*G, a.id); int j = Locate_vex(*G, b.id); //头插法 //a->b Anode* p = Create_arcnode(j, w); p->nextarc = G->vertices[i].firstarc; G->vertices[i].firstarc = p; //如果创建有向图的话,直接把下面的代码删掉即可 //b->a Anode* q = Create_arcnode(i, w); q->nextarc = G->vertices[j].firstarc; G->vertices[j].firstarc = q; } } //访问 void visit(Graph G, int index) { printf("%s ", G.vertices[index].data.id); } //输出图 void print(Graph G) { printf("以下是图的顶点连接关系:\n"); for (int i = 0; i < G.vexnum; i++) { printf("%s:", G.vertices[i].data.id); Anode* cur= G.vertices[i].firstarc; while (cur) { visit(G, cur->index); cur = cur->nextarc; } printf("\n"); } printf("顶点和边数分别是:%d %d\n", G.vexnum, G.arcnum); } 递归代码
//深度优先遍历DFS0(递归实现) void DFS0(Graph G, char* begin_id,int* visited) { int index = Locate_vex(G, begin_id); visit(G, index); visited[index] = 1;//标记这个顶点已经访问过了 Anode* p = G.vertices[index].firstarc;//找到这个顶点的下一个位置p while (p) { if (visited[p->index] == 0) {//如果没有访问过的话,就进入到下一个递归 DFS0(G, G.vertices[p->index].data.id, visited); } p = p->nextarc;//退出之后换一个方向访问 } free(visited); visited = NULL; return; }非递归代码
//深度优先遍历DFS(非递归实现) void DFS(Graph G,char* begin_id) { //判断是否变量过 int* visited = (int*)malloc(sizeof(int) * G.vexnum); memset(visited, 0, sizeof(int) * G.vexnum);//全部初始化为0 //记录路径 int* path = (int*)malloc(sizeof(int) * G.vexnum); memset(path, -1, sizeof(int) * G.vexnum); int i = -1; //初始化 int index = Locate_vex(G, begin_id); int count = 0;//表示已经访问了多少个顶点 Anode* p= G.vertices[index].firstarc;//初始化下一个位置指针p while (count<G.vexnum) { if (p) { if (visited[index] == 0) { visit(G, index); visited[index] = 1; i++; path[i] = index;//记录当前路径 p = G.vertices[index].firstarc; index = p->index;//指向下一个位置 count++; } else { p = p->nextarc; index = p->index; } } //回溯过程 else { index = path[i - 1];//返回到上一个位置 p = G.vertices[index].firstarc->nextarc;//p指针向后移动一位 index = p->index; i--; } } free(visited); free(path); path=NULL; visited = NULL; }测试结果:
int main() { Graph G; Create_graph(&G); print(G); printf("\n递归DFS0深度优先遍历:\n"); int* visited = (int*)malloc(sizeof(int) * G.vexnum); memset(visited, 0, sizeof(int) * G.vexnum); DFS0(G, "B", visited); printf("\n非递归DFS深度优先遍历:\n"); DFS(G, "B"); }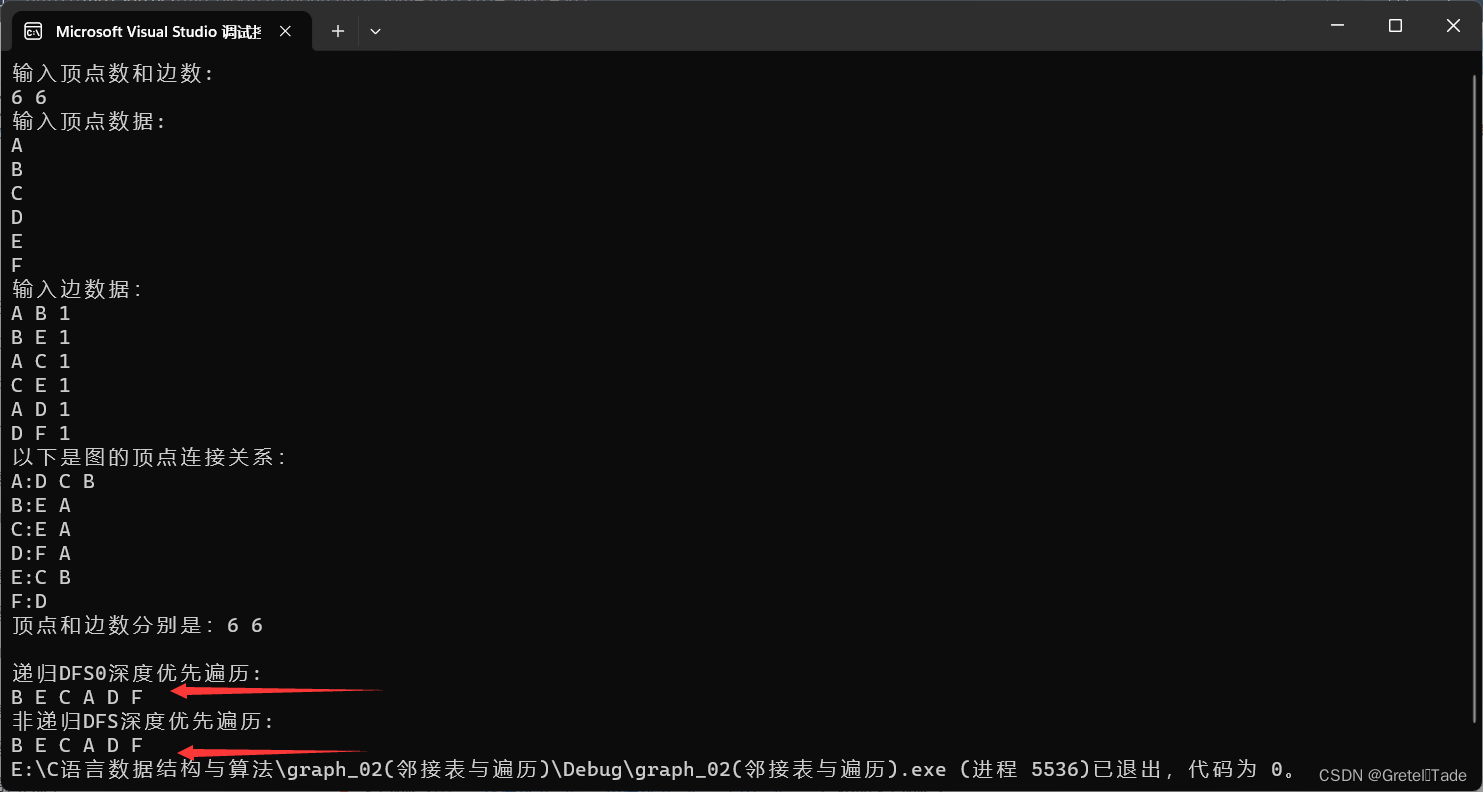
3.邻接矩阵和邻接表对比
邻接矩阵
对于一个邻接矩阵进行深度优先遍历,要把邻接矩阵上每一个点都进行对比访问,如果这个图有n个顶点的话,所以时间复杂度为O(n^2)
邻接表
用邻接表来表示图,虽然有2e个表结点,但只需扫描e个结点即可完成遍历,加上访问n个头结点的时间,时间复杂度为O(n+e)。
所以可以看出,如果是对于稠密图的话用邻接矩阵更好,而对于稀疏图的话,用邻接表会更好。
以上就是本期的全部内容了,我们下次接着学习图的广度优先遍历,下次见咯!
分享一张壁纸: 
