目录
引言:
本节我们就要进入两个数组的dp问题的学习,通过前面几个章节的学习,相信友友们对动态规划的解题步骤和代码编写步骤已经有了一定的了解(*/ω\*),接下来我会通过例题来帮助大家理解两个数组dp问题的一般解题模板,那废话不多说我们开始吧👍👍👍!

首先我先给出这类dp问题的常见的套路和状态表示如下:
两个数组的dp问题最常用的状态表示就是dp[i][j]表示选取第一个数组的(0,i)区间以及第二个数组(0,j)区间作为研究对象,利用两个表最后一个位置的状况来递推出关系,进而填写dp表。
例题1:最长公共子序列
链接:最长公共子序列
题目简介:
给定两个字符串 text1 和 text2,返回这两个字符串的最长 公共子序列 的长度。如果不存在 公共子序列 ,返回 0 。
一个字符串的 子序列 是指这样一个新的字符串:它是由原字符串在不改变字符的相对顺序的情况下删除某些字符(也可以不删除任何字符)后组成的新字符串。
- 例如,
"ace"是"abcde"的子序列,但"aec"不是"abcde"的子序列。
两个字符串的 公共子序列 是这两个字符串所共同拥有的子序列。

解法(动态规划):
1. 状态表示:
两个数组的动态规划,我们的定义状态表示的经验就是:
(1)选取第⼀个数组[0, i] 区间以及第⼆个数组[0, j] 区间作为研究对象。
(2)结合题目要求,定义状态表示。
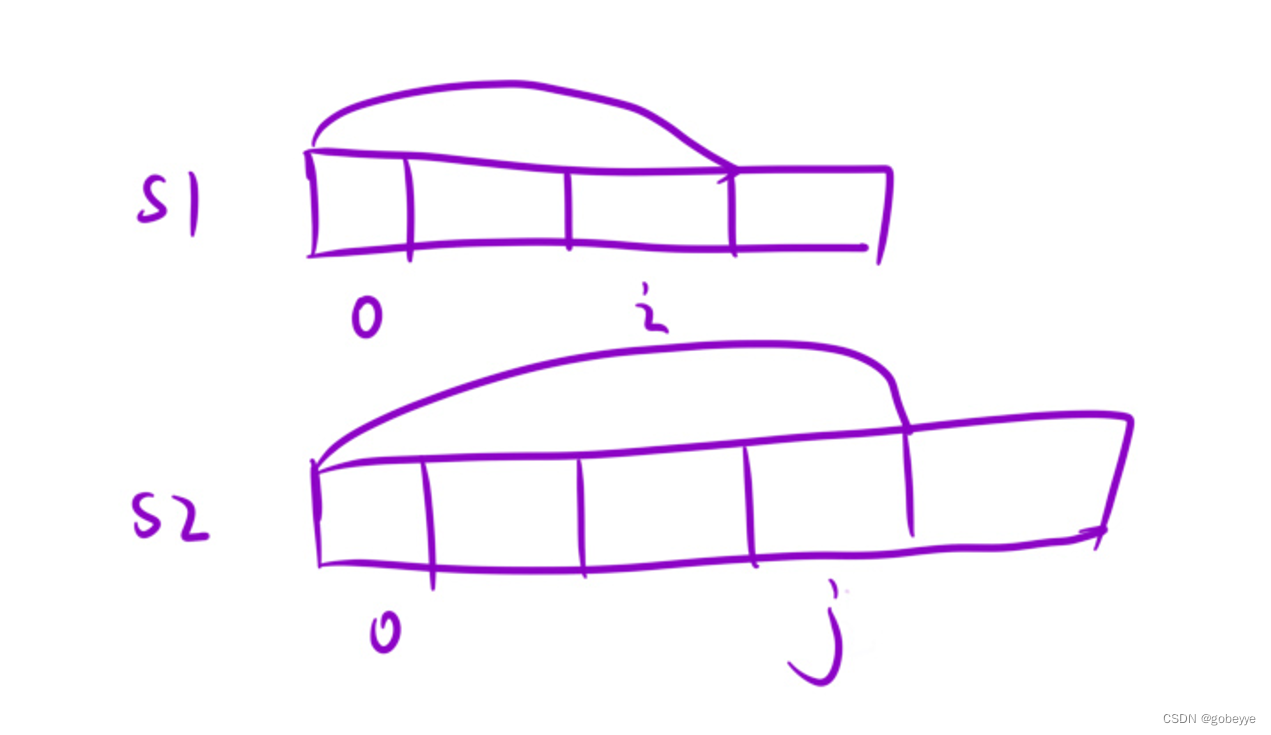
在这道题中,我们根据定义状态表示为:dp[i][j] 表示: s1 的[0, i] 区间以及s2 的[0, j] 区间内的所有的子序列中,最长公共子序列的长度。
2.状态转移方程:
分析状态转移方程的经验就是根据最后⼀个位置的状况,分情况讨论:
(1)两个字符相同, s1[i] = s2[j] :那么最长公共子序列就在s1 的[0, i - 1] 以及s2 的[0, j - 1] 区间上找到⼀个最长的,然后再加上s1[i]即可。因此dp[i][j] = dp[i - 1][j - 1] + 1 。
(2)两个字符不相同, s1[i] != s2[j] :那么最长公共子序列⼀定不会同时以s1[i]和s2[j] 结尾。那么我们找最长公共子序列时,有下面三种策略:
1.去s1 的[0, i - 1] 以及s2 的[0, j] 区间内找:此时最大长度为dp[i - 1][j] 。
2.去s1 的[0, i] 以及s2 的[0, j - 1]区间内找:此时最大长度为dp[i ][j - 1]。
3.去s1 的[0, i - 1] 以及s2 的[0, j - 1]区间内找:此时最大长度为dp[i - 1][j - 1] 。
我们要三者的最大值即可。但是我们细细观察会发现,第三种包含在第⼀种和第⼆种情况里面,但是我们求的是最大值,并不影响最终结果。因此只需求前两种情况下的最大值即可。
综上,状态转移方程为:
(1)if(s1[i] == s2[j]) dp[i][j] = dp[i - 1][j - 1] + 1 。
(2)if(s1[i] != s2[j]) dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]) 。.
3.初始化:
当s1 为空时,没有长度,同理s2也是。因此第一行和第⼀列里面的值初始化为0即可保证后续填表是正确的。当为字符串时可以再字符串前面添加一个空字符来对其我们的下标,这样我们就不用注意下标的映射关系了。

4.填表顺序:
从上往下填写每⼀行,每⼀行从左往右。
5.返回值:
返回dp[m][n]。
代码如下:
class Solution { public int longestCommonSubsequence(String text1, String text2) { //1.创建 dp 表 //2.初始化 //3.填表 //4.返回值 int n = text1.length(); int m = text2.length(); int[][] dp = new int[n + 1][m + 1]; text1 = " " + text1; text2 = " " + text2; for(int i = 1;i <= n;i++){ for(int j = 1;j <= m;j++){ if(text1.charAt(i) == text2.charAt(j)){ dp[i][j] = dp[i - 1][j - 1] + 1; }else{ dp[i][j] = Math.max(dp[i - 1][j],dp[i][j - 1]); } } } return dp[n][m]; } }时间复杂度:O(n * m)
空间复杂度:O(n * m)
例题2:不同的子序列
链接:不同的子序列
题目简介:给你两个字符串 s 和 t ,统计并返回在 s 的 子序列 中 t 出现的个数,结果需要对 109 + 7 取模。
解法(动态规划):
这题说是要取模但是实际做不用取模也可以过。
1. 状态表示:
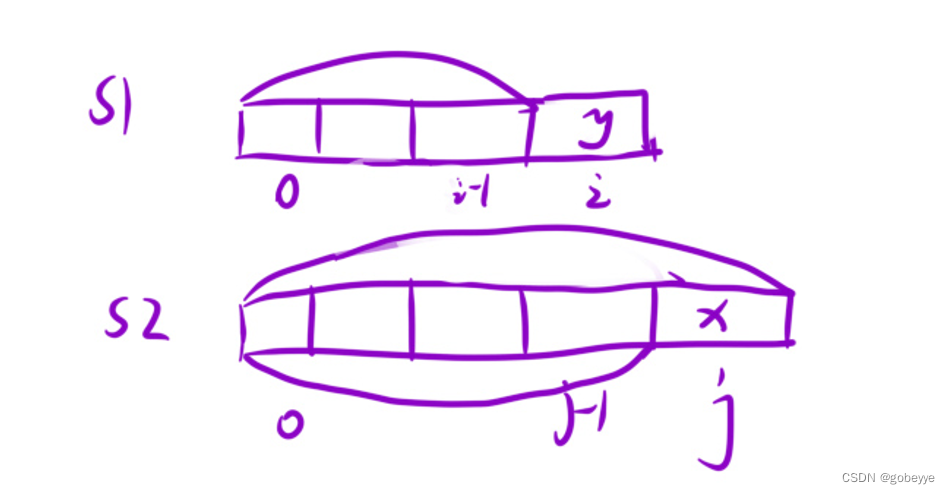
dp[i][j] 表示:在字符串 s 的 [0, j] 区间内的所有子序列中,有多少个 t 字符串 [0, i] 区间内的子串。(两个数组的dp问题状态表示一般都长这样)。
2.状态转移方程:
根据最后⼀个位置的元素来进行分类讨论和分析。
(1)当t[i] == s[j]的时候,此时的子序列有两种选择:
1.⼀种选择是:子序列选择s[j]作为结尾,此时相当于在状态dp[i - 1][j - 1]中的所有符合要求的子序列的后面,再加上⼀个字符s[j](请大家结合状态表示, 好好理解这句话),此时dp[i][j] = dp[i - 1][j - 1]。不用加一,求的是个数不是长度。
2.另⼀种选择是:我就是任性,我就不选择s[j]作为结尾。此时相当于选择了状态dp[i][j - 1] 中所有符合要求的子序列。我们也可以理解为继承了上个状态里面的求得的子序列。此时dp[i][j] = dp[i][j - 1] 。
两种情况加起来,就是 t[i] == s[j]时的结果。
(2)当t[i] != s[j] 的时候,此时的子序列只能从dp[i][j - 1] 中选择所有符合要求的子序列。只能继承上个状态里面求得的子序列, dp[i][j] = dp[i][j - 1] 。
综上所述,状态转移方程为:
(1)所有情况下都可以继承上⼀次的结果: dp[i][j] = dp[i][j - 1].
(2)当 t[i] == s[j]时,可以多选择⼀种情况: dp[i][j] += dp[i - 1][j - 1].
3.初始化:
辅助节点 + 字符串前面加一个空格,这两种初始化方法一起用。
当s为空时,t的子串中有⼀个空串和它⼀样,因此初始化第⼀行全部为1 。
4.填表顺序:
从上往下
从左往右
5.返回值:
返回dp[m][n]的值。
代码如下:
class Solution { public int numDistinct(String s, String t) { //1.创建 dp 表 //2.初始化 //3.填表 //4.返回值 //s大m //t小n int n = t.length(); int m = s.length(); int[][] dp = new int[n + 1][m + 1]; s = " " + s; t = " " + t; for(int i = 0;i <= m;i++){ dp[0][i] = 1; } for(int i = 1;i <= n;i++){ for(int j = i;j <= m;j++){ if(t.charAt(i) == s.charAt(j)){ dp[i][j] = dp[i - 1][j - 1]; } dp[i][j] += dp[i][j - 1]; } } return dp[n][m]; } }时间复杂度:O(n * m)
空间复杂度:O(n * m)
例题3:通配符匹配
链接:通配符匹配
题目简介:
给你一个输入字符串 (s) 和一个字符模式 (p) ,请你实现一个支持 '?' 和 '*' 匹配规则的通配符匹配:
'?'可以匹配任何单个字符。'*'可以匹配任意字符序列(包括空字符序列)。
判定匹配成功的充要条件是:字符模式必须能够 完全匹配 输入字符串(而不是部分匹配)。

解法(动态规划):
1. 状态表示:
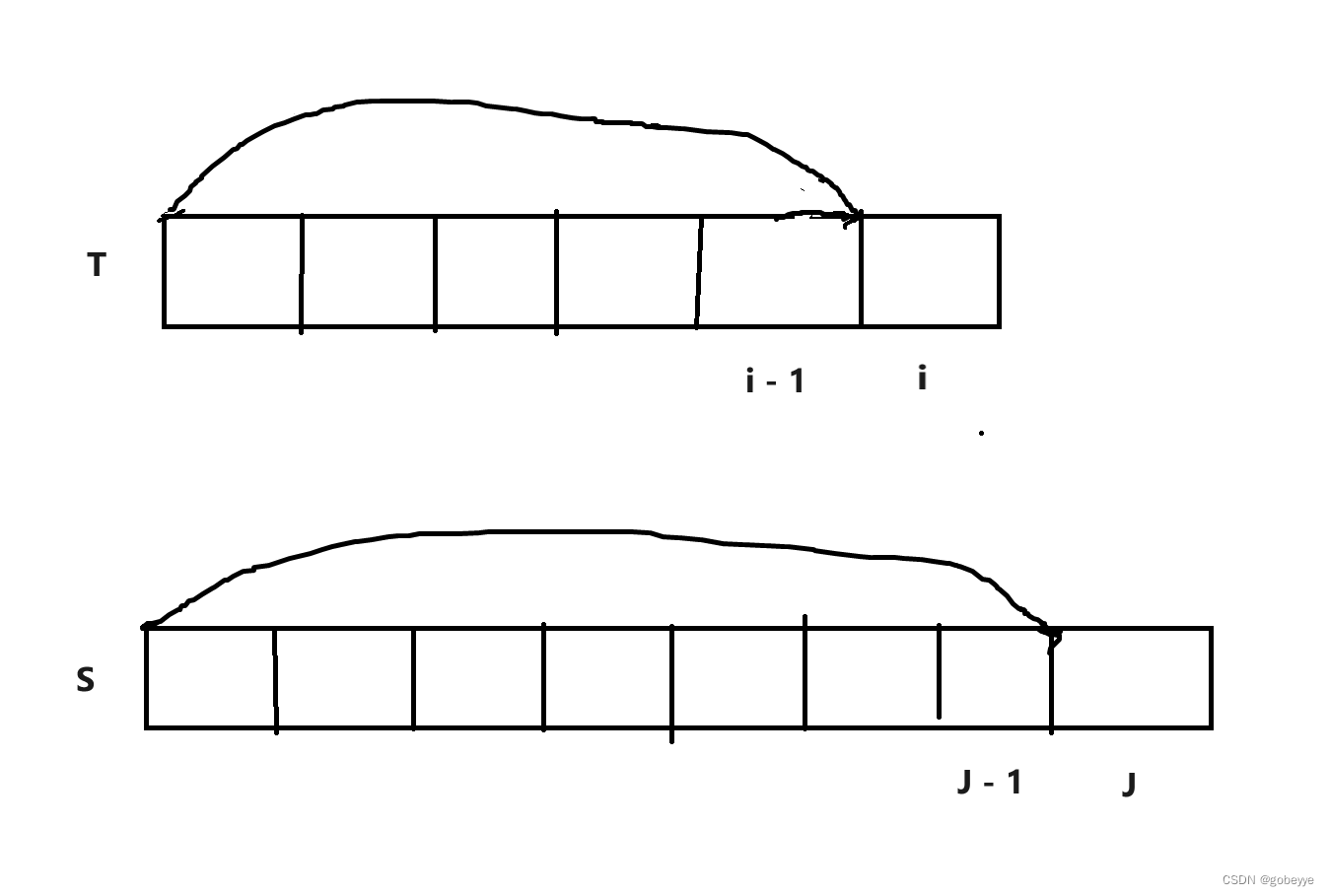
dp[i][j] 表示: p字符串[0, j] 区间内的子串能否匹配字符串s的 [0, i] 区间内的子串。
2.状态转移方程:
根据最后⼀个位置的元素来分情况讨论:
(1)当s[i] == p[j]或p[j] == '?' 的时候,此时两个字符串匹配上了当前的⼀个字符,只能从dp[i - 1][j - 1] 中看当前字符前面的两个子串是否匹配。只能继承上个状态中的匹配结果,dp[i][j] = dp[i][j - 1]
(2)当p[j] == '*' 的时候,此时匹配策略有两种选择:
1.⼀种选择是: * 匹配空字符串,此时相当于它匹配了⼀个寂寞,直接继承状态dp[i][j - 1] ,此时dp[i][j] = dp[i][j - 1] 。
2.另⼀种选择是: * 向前匹配1 ~ n 个字符,直至匹配上整个s1串。此时相当于从dp[k][j - 1]所有匹配情况中,选择性继承可以成功的情况。此时dp[i][j] = dp[k][j - 1]。
(3)当p[j] 不是特殊字符,且不与s[i]相等时,无法匹配。
综上所述,状态转移方程为:
(1)当s[i] == p[j] 或p[j] == '?' 时: dp[i][j] = dp[i][j - 1].
(2)当p[j] == '*' 时,有多种情况需要讨论: dp[i][j] = dp[k][j - 1] (0 <= k <= i).
优化:当我们发现,计算⼀个状态的时候,需要⼀个循环才能搞定的时候,我们要想到去优化。优 化的方向就是用⼀个或者两个状态来表示这⼀堆的状态。通常就是把它写下来,然后用数学的方式做一个等价替换。我们惊奇的发现, dp[i][j] 的状态转移方程里面除了第⼀项以外,其余的都可以用dp[i - 1][j]替代。因此,我们优化我们的状态转移方程为: dp[i][j] = dp[i - 1][j] || dp[i][j - 1] 。
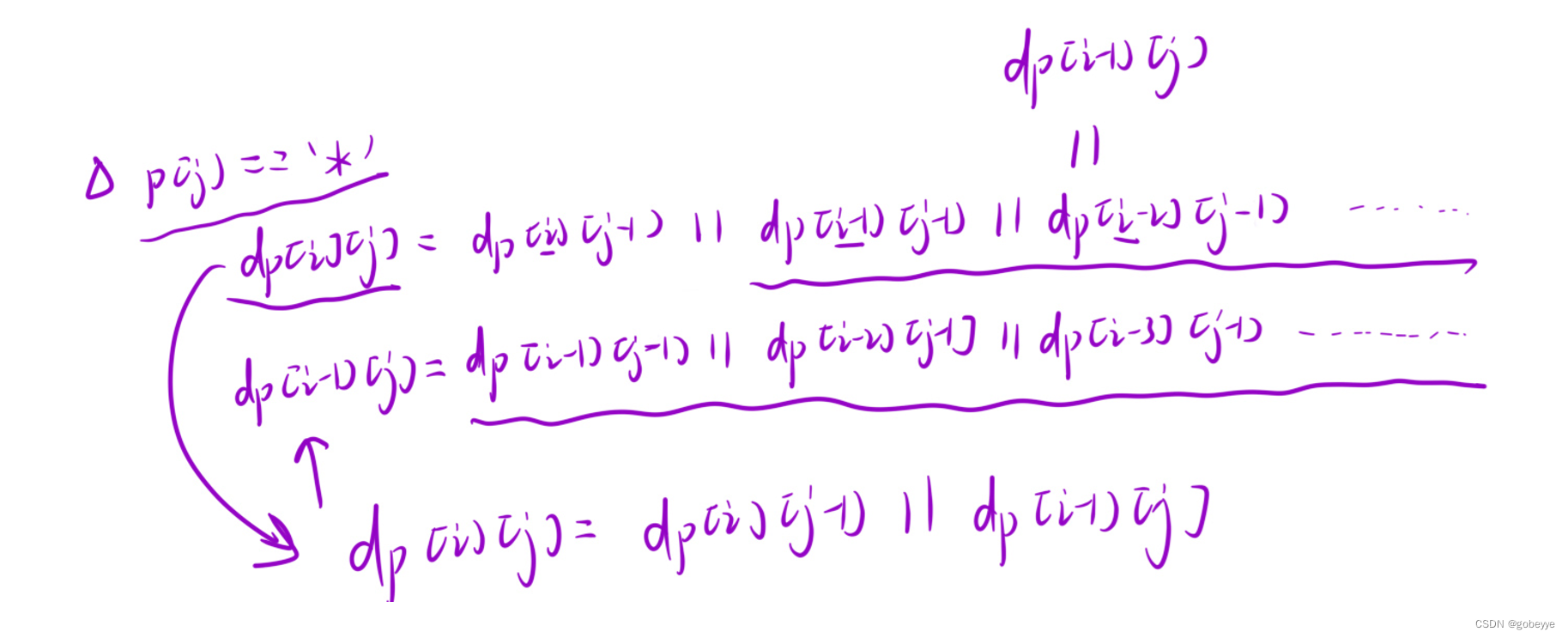
3.初始化:
(1)dp[0][0]表示两个空串能否匹配,答案是显然的,初始化为true。
(2)第一行表示s是⼀个空串, p串和空串只有⼀种匹配可能,即p串表示会为" *** " ,此时也相当于空串匹配上空串。所以,我们可以遍历p串,把所有前导为" * " 的p子串和空串的dp值设为true。
(3)第⼀列表示p是⼀个空串,不可能匹配上s 串,跟随数组初始化即可。
4.填表顺序:
从上往下填每一行,每一行从左往右。
5.返回值:
返回dp[m][n]。
对应代码如下:
class Solution { public boolean isMatch(String s, String p) { //1.创建 dp 表 //2.初始化 //3.填表 //4.返回值 //s为n //p为m int n = s.length(); int m = p.length(); boolean[][] dp = new boolean[n + 1][m + 1]; s = " " + s; p = " " + p; boolean tmp = true; dp[0][0] = true; for(int i = 1;i <= m;i++){ if(p.charAt(i) != '*'){ tmp = false; } dp[0][i] = tmp; } for(int i = 1;i <= n;i++){ for(int j = 1;j <= m;j++){ if(p.charAt(j) == '?'){ dp[i][j] = dp[i - 1][j - 1]; }else if(p.charAt(j) == '*'){ dp[i][j] = dp[i][j - 1] || dp[i - 1][j]; }else{ dp[i][j] = (s.charAt(i) == p.charAt(j)) && dp[i -1][j - 1]; } } } return dp[n][m]; } }例题4:正则表达式
链接:正则表达式
题目简介:
给你一个字符串 s 和一个字符规律 p,请你来实现一个支持 '.' 和 '*' 的正则表达式匹配。
'.'匹配任意单个字符'*'匹配零个或多个前面的那一个元素
所谓匹配,是要涵盖 整个 字符串 s的,而不是部分字符串。

解法(动态规划):
1. 状态表示:
dp[i][j] 表示:字符串p的[0, j]区间和字符串s的[0, i]区间是否可以匹配。
2.状态转移方程:
(1)当s[i] == p[j] 或p[j] == '.' 的时候,此时两个字符串匹配上了当前的⼀个字符, 只能从dp[i - 1][j - 1] 中看当前字符前面的两个子串是否匹配。只能继承上个状态中的匹配结果, dp[i][j] = dp[i - 1][j - 1]。
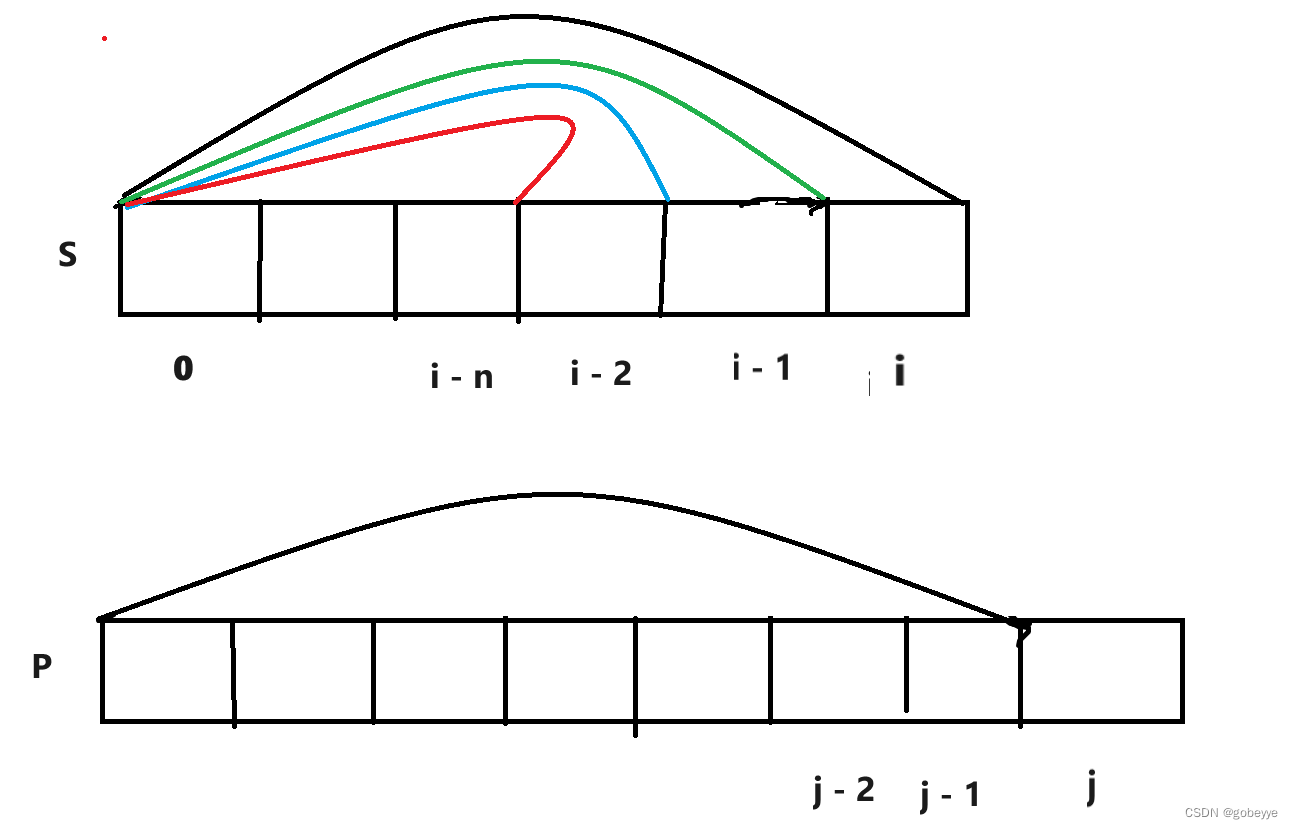
(2)当p[j] == '*' 的时候,和上道题稍有不同的是,上道题"*" 本身便可匹配0 ~ n 个字符,但此题是要带着p[j - 1]的字符⼀起,匹配0 ~ n 个和p[j - 1] 相同的字符。此时,匹配策略有两种选择:
1.⼀种选择是: p[j - 1]* 匹配空字符串,此时相当于两个字符串什么都没有匹配,直接继承状态dp[i][j - 2] ,此时dp[i][j] = dp[i][j - 2]。
2.另⼀种选择是: p[j - 1]* 向前匹配1 ~ n 个字符,直至匹配上整个s1串。此时相当于从dp[k][j - 2] 中所有匹配情况中,选择性继承可以成功的情况。此时dp[i][j] = dp[k][j - 2]。
(3)当p[j] 不是特殊字符,且不与s[i]相等时,无法匹配。
综上所述,状态转移方程为:
(1)当s[i] == p[j] 或p[j] == '.' 时: dp[i][j] = dp[i][j - 1].
(2)当p[j] == '*' 时,有多种情况需要讨论: dp[i][j] = dp[i][j - 2] ; dp[i][j] = dp[k][j - 1].
优化和第三题一样也是用等价替换,把后面多种情况归结成一种表达式。
3.初始化:
第一行表示s 是⼀个空串, p 串和空串只有⼀种匹配可能,即p串全部字符表示为"任⼀字符 + * ",此时也相当于空串匹配上空串。所以,我们可以遍历p串,把所有前导为"任⼀字符+ * " 的p子串和空串的dp值设为true。
for(int i = 2;i <= m;i += 2){ if(p.charAt(i) != '*'){ break; } dp[0][i] = true; }4.填表顺序:
从上往下填每一行,每一行从左往右。
5.返回值:
根据状态表示,返回dp[m][n]的值。
代码如下:
class Solution { public boolean isMatch(String s, String p) { //1.创建 dp 表 //2.初始化 //3.填表 //4.返回值 //s为n //p为m int n = s.length(); int m = p.length(); boolean[][] dp = new boolean[n + 1][m + 1]; s = " " + s; p = " " + p; for(int i = 2;i <= m;i += 2){ if(p.charAt(i) != '*'){ break; } dp[0][i] = true; } dp[0][0] = true; for(int i = 1;i <= n;i++){ for(int j = 1;j <= m;j++){ if(p.charAt(j) != '*'){ dp[i][j] = (p.charAt(j) == '.' || p.charAt(j) == s.charAt(i)) && dp[i - 1][j - 1]; }else{ dp[i][j] = (dp[i][j - 2]) || (p.charAt(j - 1) == s.charAt(i) || p.charAt(j - 1) == '.') && dp[i - 1][j]; } } } return dp[n][m]; } }结语:
其实写博客不仅仅是为了教大家,同时这也有利于我巩固知识点,和做一个学习的总结,由于作者水平有限,对文章有任何问题还请指出,非常感谢。如果大家有所收获的话还请不要吝啬你们的点赞收藏和关注,这可以激励我写出更加优秀的文章。

