【算法基础】拓扑排序及实战

一 、概览

这里涉及到图的概念，感兴趣的同学请移驾 –>图<–
下面还有两个相关概念，大概说一下：

1.1 有向无环图

定义：在图论中，如果一个有向图从任意顶点出发无法经过若干条边回到该点，则这个图是一个有向无环图（DAG，Directed Acyclic Graph）
每条边都带有从一个顶点指向另一个顶点的方向的图为有向图。有向图中的道路为一系列的边，系列中每条边的终点都是下一条边的起点。
如果一条路径的起点是这条路径的终点，那么这条路径就是一个环。有向无环图即为没有环出现的有向图

1.2 拓扑结构

定义：将实体抽象成点，将实体间的链接抽象成线，进而以图形的关系呈现这些点与线之间的关系。其目的在于研究这些点、线之间的相连关系。表示点和线之间关系的图被称为拓扑结构 图

比较常用的是网络拓扑结构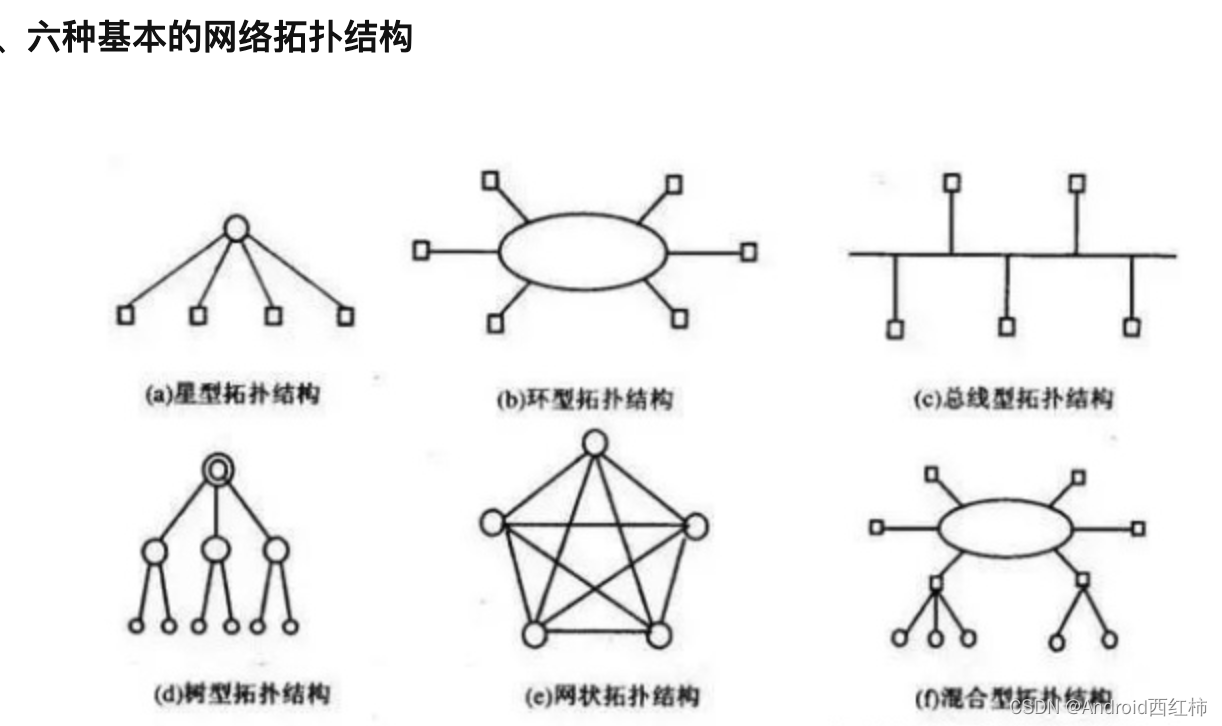

背景：
一个较大的工程往往被划分成许多子工程，我们把这些子工程称作活动(activity)。在整个工程中，有些子工程(活动)必须在其它有关子工程完成之后才能开始，也就是说，一个子工程的开始是以它的所有前序子工程的结束为先决条件的，但有些子工程没有先决条件，可以安排在任何时间开始。为了形象地反映出整个工程中各个子工程(活动)之间的先后关系，可用一个有向图来表示，图中的顶点代表活动(子工程)，图中的有向边代表活动的先后关系，即有向边的起点的活动是终点活动的前序活动，只有当起点活动完成之后，其终点活动才能进行。通常，我们把这种顶点表示活动、边表示活动间先后关系的有向图称做顶点活动网(Activity On Vertex network)，简称AOV网。

二、拓扑排序（顶点的线性排序）

定义：在图论中，拓扑排序（Topological Sorting）是一个有向无环图（DAG, Directed Acyclic Graph）的所有顶点的线性序列。

例如，一个项目包括A、B、C、D四个子部分来完成，并且A依赖于B和D，C依赖于D。现在要制定一个计划，写出A、B、C、D的执行顺序。这时，就可以利用到拓扑排序，它就是用来确定事物发生的顺序的。

且该序列必须满足下面两个条件：

• 每个顶点出现且只出现一次。
• 若存在一条从顶点 A 到顶点 B 的路径，那么在序列中顶点 A 出现在顶点 B 的前面。
• 有向无环图（DAG）才有拓扑排序

度数： 由一个顶点出发，有几条边就称该顶点有几度，或者该顶点的度数是几
出度： 由一个顶点出发的边的总数
入度： 指向一个顶点的边的总数

拓扑排序使用深度优先算法，时间复杂度为O ( V + E )

拓扑排序通常有几种实现方式：

2.1 入度表（直接遍历）

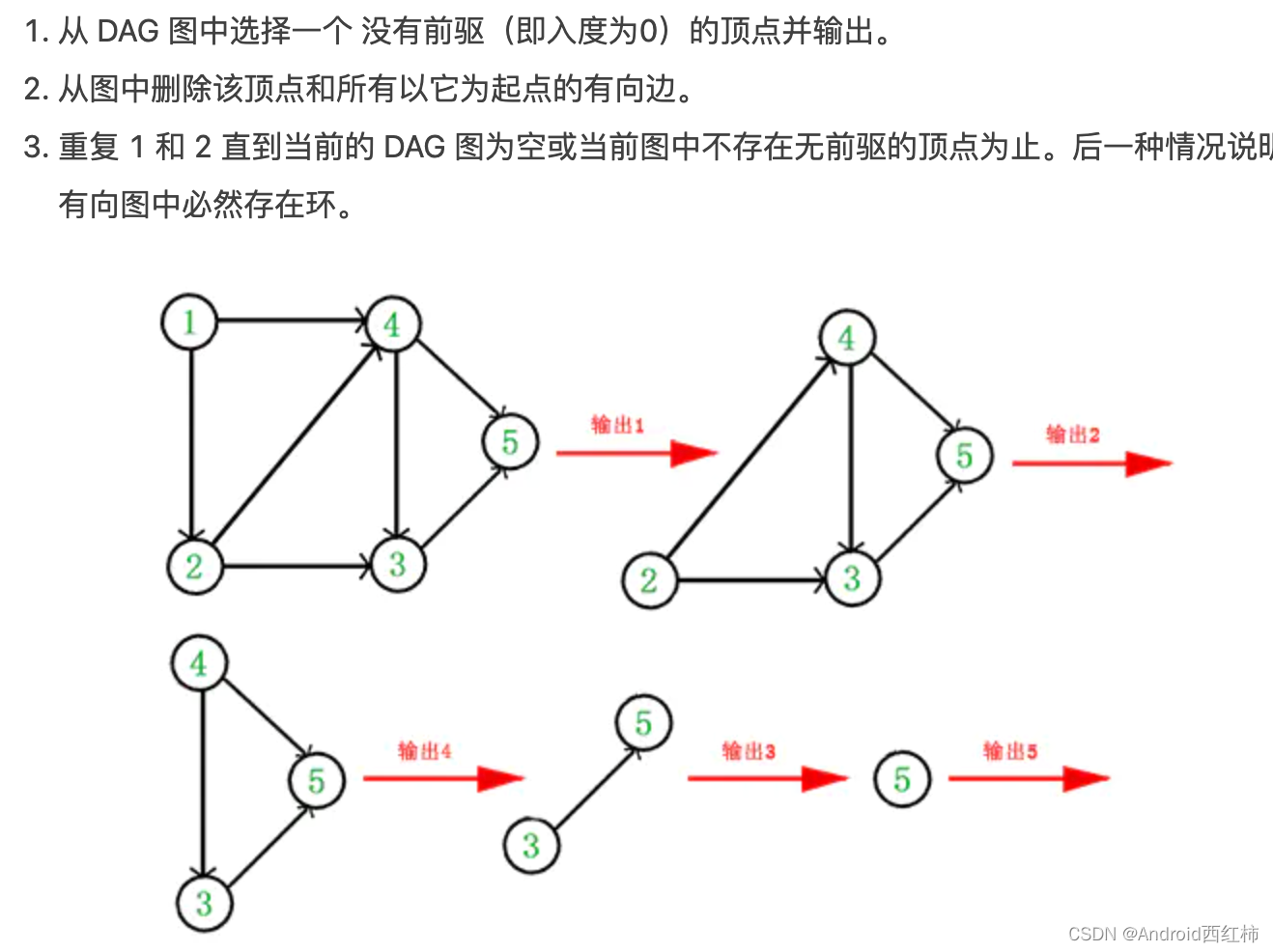
于是，得到拓扑排序后的结果是 { 1, 2, 4, 3, 5 }。
通常，一个有向无环图可以有一个或多个拓扑排序序列。

2.2 通过DFS(深度)和栈实现

思路：

找到顶点，递归遍历到最后的结点，通过回溯将遍历到的点入栈，那么先进栈的必定是只有入度的结点，只有出度的结点必定在最后进栈，最后通过出栈可以得到排序后的顺序。

具体代码请看 实战 2

2.3 通过队列实现

思路：

• 通过遍历，将所有入度为0的进入队列。并将与之相连的结点的入度-1。
• 然后一个一个的出队列，出队列的同时判断与出队列结点相连的结点是否入度为0，为0则进栈。
• 循环第一二步，直到所有节点被选择或者栈空。（其实栈空的时候，所有节点就是被选择了）

不废话，直接上代码：

/**  * 图的存储  * 邻接矩阵 二维数组  */ public static class GrapMatrix {       /**      * 节点个数      */     public int size;      /**      * 顶点名称      */     char [] nodeName;      /**      * 排序后的顺序      */     List result;      /**      * 图关系矩阵      */     int [][] matrix;      /**      *      * @param nodeName 节点      * @param edgs 节点关系      */     public GrapMatrix(char[] nodeName, char[][] edgs) {         size = nodeName.length;         this.nodeName = nodeName;         // 设置图关系矩阵大小         this.matrix = new int[size][size];         result = new ArrayList<Integer>();          // 初始化图关系矩阵         for (char[] node: edgs) {             matrix[getPosition(node[0])][getPosition(node[1])] = 1;             System.out.println(node);         }          // 输出图的邻接矩阵         for(int i = 0; i < size; i ++) {             for (int j = 0; j < size; j ++) {                 System.out.print(matrix[i][j] + " ");             }             System.out.println("");         }     }      // 排序     public void tuopuSort() {         System.out.println("\n");         // 一个一维数组，用来保存顶点的入度         int indegree[] = new int[size];         boolean indegreeV[] = new boolean[size];           // 给入度输入值         for(int i = 0; i < size; i ++) {             indegreeV[i] = false;             for (int j = 0; j < size; j ++) {                 if (matrix[i][j] == 1) {                     indegree[j] = indegree[j] + 1;                 }             }         }         System.out.println("\n");          //开始进行遍历         LinkedList<String> nodes = new LinkedList<String>();          // 将入度为 0 的节点入队列         for (int x = 0; x < size; x ++) {             if (indegree[x] == 0) {                 System.out.println(nodeName[x]);                 nodes.add(String.valueOf(nodeName[x]));             }         }          int j = 0;         while (!nodes.isEmpty()) {             for (int x = 0; x < size; x ++) {                 System.out.println("\n 数组 x = " + x + ", ");                 if (indegree[x] == 0 && !indegreeV[x]) {                      indegreeV[x] = true;                     String s = nodes.poll();                     System.out.println("add = " +s);                     result.add(s);                      // 找到跟它相关的节点,，入度 -1                     for (int y = 0; y < size; y ++) {                         if (matrix[x][y] == 1) {                             System.out.println("相关的节点 -1 = " + y);                             indegree[y] = indegree[y] - 1;                             if (indegree[y] == 0) {                                 System.out.println("相关的节点 -1 后， 入度为0， " + nodeName[y]);                                 nodes.add(String.valueOf(nodeName[y]));                             }                         }                     }                 } else {                  }             }             j ++;         }           System.out.println(result);      }      public int getPosition(char pos) {         for (int i = 0; i < nodeName.length; i ++) {             if (nodeName[i] == pos) {                 return i;             }         }         return -1;     } } 

三、实战

应用：
拓扑排序通常用来“排序”具有依赖关系的任务。
eg： 关键路径
选课系统
等这些任务有先后顺序的图。

      比如，要想升职加薪，就要先拍马屁 

3.1 选课系统

我们现在以课程排序来做代码测试，
假定一个计算机专业的学生必须完成下图所列出的全部课程。
在这里，课程代表活动，学习一门课程就表示进行一项活动，学习每门课程的先决条件是学完它的全部先修课程。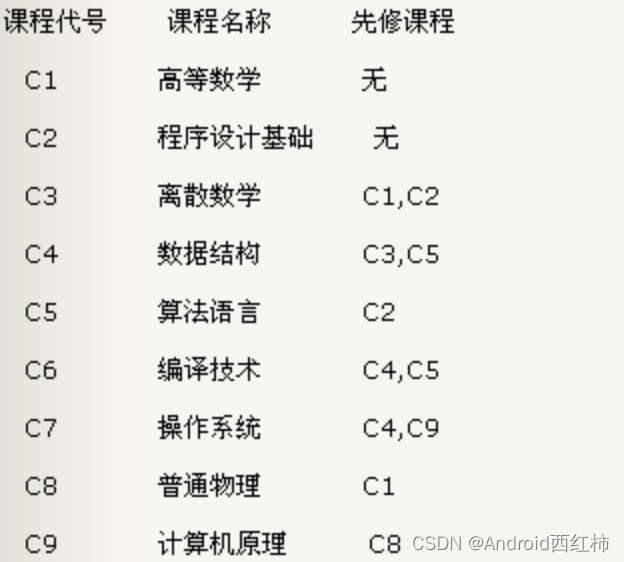

我们用图的方式，将他们的先后顺序及依赖关系表示如下：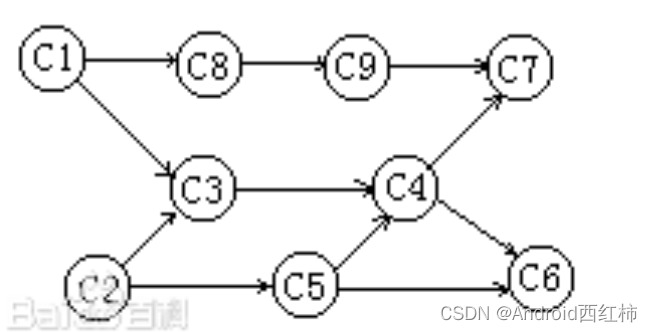

对于—> 图 的存储结构，常用的是"邻接矩阵"和"邻接表"，

拓扑排序的动态表示
https://www.cs.usfca.edu/~galles/visualization/TopoSortIndegree.html

3.2 Android冷启动优化，有向无环图启动器

Application中初始化应用所需的业务、工具、UI等组件，导致耗时，导致冷启动会比较慢，需要进行优化处理，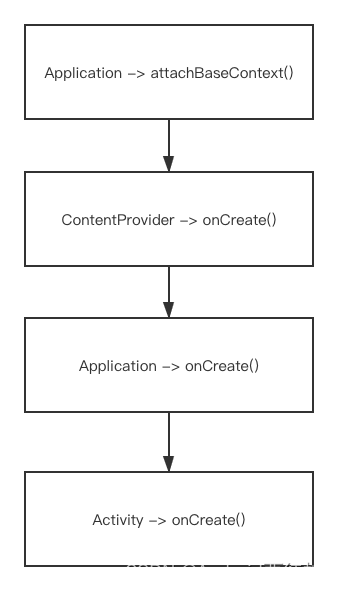

我们要做的就是把主线程的串行任务变成并发任务，在将所有任务整理出来后，进行一个排序，

1、每一个业务模块当成一个任务，再梳理任务之间的关系。有的必须要在所以任务之前初始化，有的必须要在主线程初始化，有的可以有空在初始化，有的必须要在有的任务执行完毕再初始化，将这些任务的先后顺序及依赖关系用图画出来。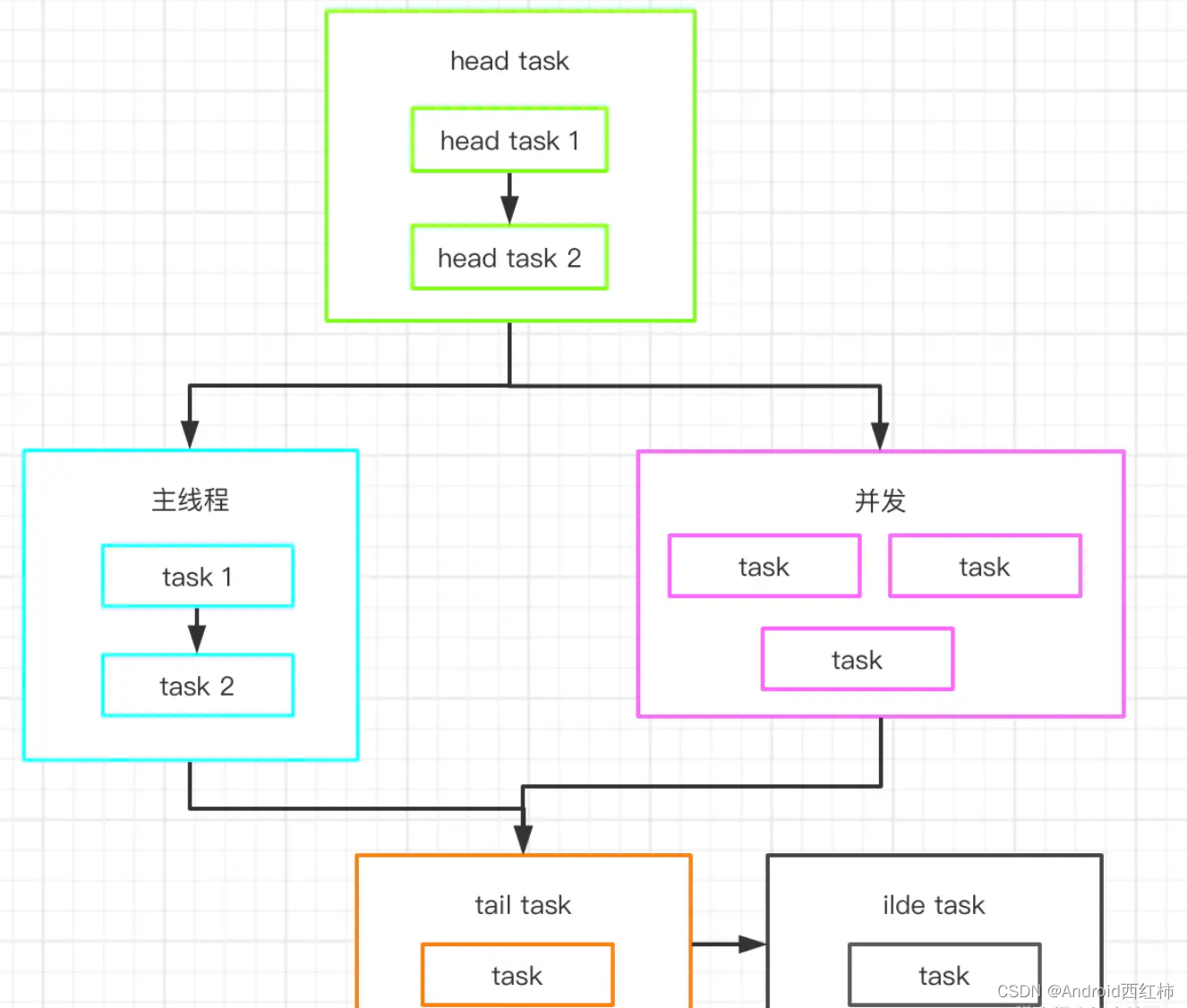

主进程执行， eg：推送，就不需要判断进程
主线程执行，eg：有的要主线程，有的要子线程

2、代码Task化，启动逻辑抽象为Task；
3、根据所有任务依赖关系排序生成一个有向无环图；
4、多线程按照排序后的优先级依次执行

关健代码

public class AppStartTaskSortUtil {     /**      * 拓扑排序      * taskIntegerHashMap每个Task的入度（key= Class < ? extends AppStartTask>）      * taskHashMap每个Task            （key= Class < ? extends AppStartTask>）      * taskChildHashMap每个Task的孩子  （key= Class < ? extends AppStartTask>）      * deque 入度为0的Task      */     public static List<AppStartTask> getSortResult(List<AppStartTask> startTaskList, HashMap<Class<? extends AppStartTask>, AppStartTask> taskHashMap, HashMap<Class<? extends AppStartTask>, List<Class<? extends AppStartTask>>> taskChildHashMap) {         List<AppStartTask> sortTaskList = new ArrayList<>();         HashMap<Class<? extends AppStartTask>, TaskSortModel> taskIntegerHashMap = new HashMap<>();         Deque<Class<? extends AppStartTask>> deque = new ArrayDeque<>();         for (AppStartTask task : startTaskList) {             if (!taskIntegerHashMap.containsKey(task.getClass())) {                 taskHashMap.put(task.getClass(), task);                 taskIntegerHashMap.put(task.getClass(), new TaskSortModel(task.getDependsTaskList() == null ? 0 : task.getDependsTaskList().size()));                 taskChildHashMap.put(task.getClass(), new ArrayList<Class<? extends AppStartTask>>());                 //入度为0的队列                 if (taskIntegerHashMap.get(task.getClass()).getIn() == 0) {                     deque.offer(task.getClass());                 }             } else {                 throw new RuntimeException("任务重复了: " + task.getClass());             }         }         //把孩子都加进去         for (AppStartTask task : startTaskList) {             if (task.getDependsTaskList() != null) {                 for (Class<? extends AppStartTask> aclass : task.getDependsTaskList()) {                     taskChildHashMap.get(aclass).add(task.getClass());                 }             }         }         //循环去除入度0的，再把孩子入度变成0的加进去         while (!deque.isEmpty()) {             Class<? extends AppStartTask> aclass = deque.poll();             sortTaskList.add(taskHashMap.get(aclass));             for (Class<? extends AppStartTask> classChild : taskChildHashMap.get(aclass)) {                 taskIntegerHashMap.get(classChild).setIn(taskIntegerHashMap.get(classChild).getIn() - 1);                 if (taskIntegerHashMap.get(classChild).getIn() == 0) {                     deque.offer(classChild);                 }             }         }         if (sortTaskList.size() != startTaskList.size()) {             throw new RuntimeException("出现环了");         }         return sortTaskList;     } }