【最短路算法】第二弹：一文弄懂Bellman-Ford(贝尔曼福特算法)_业界新闻

发布时间:2024-07-19 23:11

阅读量:2

博主简介：努力学习的大一在校计算机专业学生，热爱学习和创作。目前在学习和分享：算法、数据结构、Java等相关知识。
博主主页：@是瑶瑶子啦
所属专栏:算法；该专栏专注于蓝桥杯和ACM等算法竞赛🔥
近期目标：写好专栏的每一篇文章

💐前言

前天，我们学习了Dijkstra算法：【最短路算法】一篇文章彻底弄懂Dijkstra算法|多图解+代码详解
Dijstra算法用于计算单源、正权边的最短路问题
今天学习的贝尔曼福特算法，是用于计算单源，且可含负权边的最短路问题

🌻一、Bellman-Ford算法简介

用于求解单源、有负权边的最短路问题
实现通过m次迭代求出从起点到终点不超过m条边构成的最短路径
其优于Dijkstra的方面是边的权值可以为负数、实现简单，缺点是时间复杂度过高。时间复杂度是O(nm)

🍼与迪杰斯特拉算法的区别：

迪杰斯特拉算法是借助贪心思想，每次选取一个未处理的最近的结点，去对与他相连接的边进行松弛操作；贝尔曼福特算法是直接对所有边进行N-1遍松弛操作。
迪杰斯特拉算法要求边的权值不能是负数；贝尔曼福特算法边的权值可以为负数，并可检测负权回路。

名词解释：
1. 松弛操作：不断更新最短路径和前驱结点的操作。
2. 负权回路：绕一圈绕回来发现到自己的距离从0变成了负数，到各结点的距离无限制的降低，停不下来

🌻二、算法思路

🛫思路

初始化源点s到各个点v的路径dis[v] = ∞，dis[s] = 0。
进行n - 1次遍历，每次遍历对所有边进行松弛操作，满足则将权值更新。
松弛操作：以a为起点，b为终点，ab边长度为w为例。dis[a]代表源点s到a点的路径长度，dis[b]代表源点s到b点的路径长度。如果满足下面的式子则将dis[b]更新为dis[a] + w。
dis[b] > dis[a] + w
遍历都结束后，若再进行一次遍历，还能得到s到某些节点更短的路径的话，则说明存在负环路。

🌱算法模板

int n, m;       // n表示点数，m表示边数 int dist[N];        // dist[x]存储1到x的最短路距离  struct Edge     // 边，a表示出点，b表示入点，w表示边的权重 {     int a, b, w; }edges[M];  // 求1到n的最短路距离，如果无法从1走到n，则返回-1。 int bellman_ford() {     memset(dist, 0x3f, sizeof dist);     dist[1] = 0;      // 如果第n次迭代仍然会松弛三角不等式，就说明存在一条长度是n+1的最短路径，由抽屉原理，路径中至少存在两个相同的点，说明图中存在负权回路。     for (int i = 0; i < n; i ++ )     {         for (int j = 0; j < m; j ++ )         {             int a = edges[j].a, b = edges[j].b, w = edges[j].w;             if (dist[b] > dist[a] + w)                 dist[b] = dist[a] + w;         }     }      if (dist[n] > 0x3f3f3f3f / 2) return -1;     return dist[n]; }

总结

Bellman-ford算法的思路也很简单，直接就是两层循环，内层循环所有边，外层循环就是循环所有边的次数，这个外层循环次数一般是题目控制的。时间复杂度是O(n*m)

🚏注意点

循环n次之后对所有的边一定满足dist[b]<=dist[a]+w，这个叫”三角不等式”
如果图中经过源点到目的点，有负权回路的话，最短路就不一定存在了
💥迭代次数是有实际意义的，比如我们迭代了k次，那么我们求的最短距离就是从源点点经过不超过k条边走到n号点的最短距离;所以在第n次迭代的时候又更新了某些边的话，就说明路径中一定存在环，并且是负权回路。因为第n次迭代在不存在负权回路的情况下是遍历到第n号点了，后面是没有点了，如果还能更新，说明路径中存在回路，而且是负权回路。

🌻二、算法原理

🥘核心思想: 松弛操作

松弛法（relaxation）是一数学术语，描述的是一些求解方法，这些方法会通过逐步接近的方式获得相关问题的最佳解法。每运用一次松弛法就好像我们“移动”了一次，而我们要做的就是在尽可能少的移动次数内找到最佳解决方案。

👩‍🏫为啥能求最短路？为啥迭代次数有意义？

首先，Bellman算法的核心是松驰，和Dijsktra算法不一样，Djikstra算法是松驰+贪心（，其实质就是在问相应边对面的顶点————“你能够被改进（更短）吗？”）

最短路算法的本质，都是在研究松驰的顺序！通过不断的松驰，最终求得每个顶点的最短路

Dijkstra松驰顺序，是依次松驰距离源点距离最短的未被处理过的点与之相连的顶点。是以一种贪心策略进行松驰的。这种特点导致，一旦某个顶点被处理过（即对与它相连的顶点进行松驰），那么后面该顶点自己被松驰，但是与它相连的顶点不能因为它的松驰而松驰，导致出现不准确的结果。（当边全为正，是不会出现这种情况，因为在松驰与该顶点相连的顶点时，这种算法已经保证了该点已经被松驰到极限）。
Bellman算法的核心就是松驰，没有贪心策略，也使它的时间复杂度比较高。因为它是单纯的松驰。首先我们要明白的是：如果处于第n层的节点，在它上一层的即n-1层所以节点的dist已经确定为最终真实值，那么通过一次遍历，第n层节点的dist也能被确定为最终真实值。第一次迭代，获得的信息是：与源点相邻点的真正dist（第二层节点），（其他点的可能仍为无穷大，或者为松驰一次状态）；第二次循环，因为第二层的信息已经完全掌握，此次迭代是能确定第三层节点（从源点出发，经过2条边）的点的真实最短距离。（由于遍历的过程中，只完全掌握了第一层，其他节点的dist不能完全确定为最终的dist);如此循环，遍历n-1次，第n层的节点已经遍历完，至此，所有节点的dist都最终确定了（解释了为啥能求最短路)。
经过上面的分析，可以得出，bellman的松驰顺序是的策略是，暴力遍历，无脑松驰。
图解

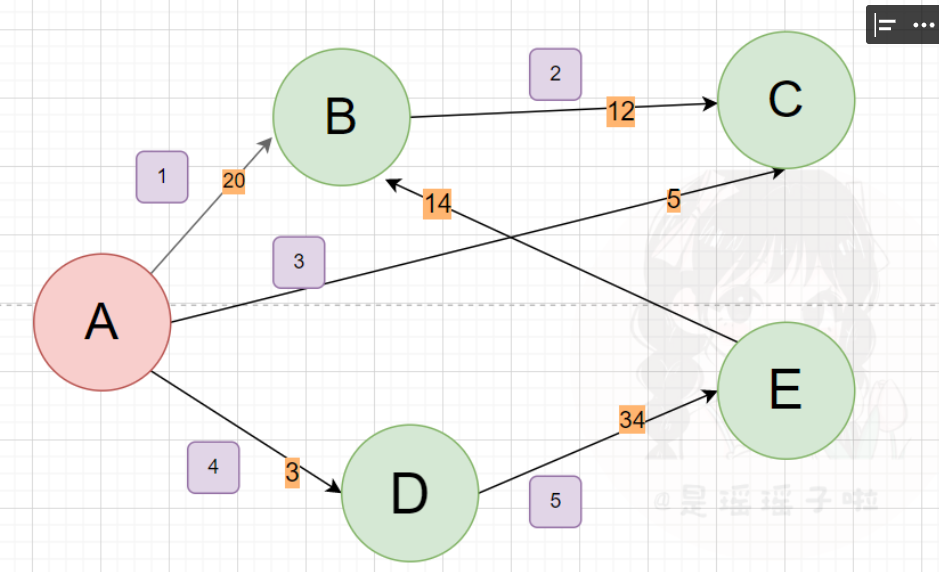
👩‍🏫串联问题

串联问题一般发生在求解有边数限制的最短路问题中（下面有例题），这里我们主要讲一下原理和解决办法

其实理解了上面的过程，串联也好解释。因为在遍历的过程中，虽然说第二层的节点的dist可能任然为初始化的正无穷，但是由于第一层的更新和第二层的更新是同时的，很有可能更新完某个第一层节点，恰好后面去更新与它相连的第二层节点，那么该第二层节点的dist由于第一层节点的更新也更新了（如果该第二层节点同时也是处于第一层位置），看下面例子
防止串联，其实就是防止在第k次循环，更新k+1层节点时，由于k+1层节点的更新和确定，以k+1更新后的结果为基础松驰了与之相连的下一层的某个节点。！

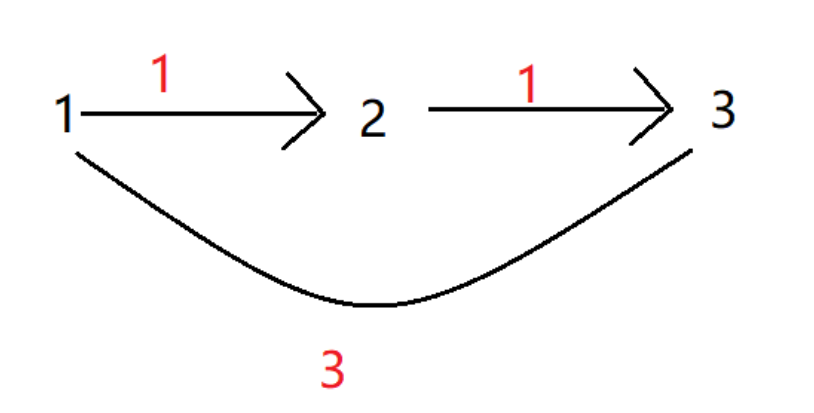
可以发现，如果我们没有备份上一次的dist数组的话，限制从1出发不超过1条边到3最短距离本应该是3，但变成了2。内层循环只迭代了一次，但是在更新的过程中会发生”串联”
为什么是发生呢？我们来分析一下
假设每次迭代，遍历所有边，遍历边的顺序如下：
1→2, 1→3, 2→3
遍历完第一条边dist[2] = 1,遍历完第二条边dist[3] = 3,遍历第三条边，由于1→2的dist已经确定，在掌握这个信息的前提下，发生串联，dist[3]可以直接松驰，更新为dist[3] = 2,但这不是我们想要的答案。我们想要的是：迭代k次，得到从源点出发，不超过k条边的最短路。
怎么保证不发生串联呢？我们保证更新的时候只用上一次循环的结果就行。所以我们先备份一下。备份之后backup数组存的就是上一次循环的结果，我们用上一次循环的结果来更新距离。所以我们这样写dist[b]=min(dist[b],backup[a]+w)来更新距离，而不是dist[b]=min(dist[b],dist[a]+w)，这样写就会发生上面说的”串联”现象。
假如我们现在是第k次迭代，那么backup保留的是第k-1次迭代后获得的信息。
在这个例子中，backup保留的是没有迭代之前（比如站在3的视角，它不会知道1→2的距离，即使1→2的距离在2→3之前更新，这样就不会因为1→2dist的确定，而串联确定2→3)

🌻三、加深理解-题目训练

bellman-ford算法虽然时间复杂度比较高，但它独特的性质（本质上还是松驰顺序），使它非常适合做：有限制边数的最短路。因为上面已经讲到，它的迭代次数是有意义的，第k次迭代，在防止串联的情况下，代表从源点出发，经过不超过k条边，所经过的顶点距离源点的最短距离被百分之百确定好了。

AcWing 853. 有边数限制的最短路

给定一个 n 个点 m 条边的有向图，图中可能存在重边和自环， 边权可能为负数。

请你求出从 1 号点到 n 号点的最多经过 k 条边的最短距离，如果无法从 1 号点走到 n 号点，输出 impossible。

注意：图中可能 存在负权回路 。

输入格式

第一行包含三个整数 n,m,k。

接下来 m 行，每行包含三个整数 x,y,z，表示存在一条从点 x 到点 y 的有向边，边长为 z。

点的编号为 1∼n。

输出格式

输出一个整数，表示从 1 号点到 n 号点的最多经过 k 条边的最短距离。

如果不存在满足条件的路径，则输出 impossible。

数据范围

1≤n,k≤500,
1≤m≤10000,
1≤x,y≤n，
任意边长的绝对值不超过 10000。

输入样例：

3 3 1 1 2 1 2 3 1 1 3 3

输出样例：

👩‍🏫详细注释题解

#include <cstring> #include <iostream> #include <algorithm>  using namespace std;  const int N = 510, M = 10010;//最大点数和边数  int n,m,k;//实际点数和边数 int dist[N],last[N];//备份数组，作用是防止串联  struct Edge{     int a,b,w;//存a->b权重是w的边 }edges[M];//结构体数组，用来存边  void bellman_ford(){     memset(dist,0x3f,sizeof(dist));//初始化dist数组     dist[1] = 0;          for(int i = 0; i < k; i ++){        memcpy(last, dist, sizeof(dist));//备份数组，备份上次迭代的dist数组        for (int j = 0; j < m; j++){//遍历所有边             auto e = edges[j];             dist[e.b] = min(dist[e.b],last[e.a] + e.w);//松驰操作        }     } }  int main(){      scanf("%d%d%d",&n,&m,&k);//n个顶点，m条边，k是限制边数            for(int i = 0; i < m; i++){          int a,b,w;          scanf("%d%d%d",&a,&b,&w);          edges[i] = {a,b,w};      }            bellman_ford();            if(dist[n] > 0x3f3f3f3f / 2) puts("impossible");      else printf("%d\n",dist[n]);           return 0; }