特征映射(机器学习)_业界新闻

发布时间:2024-07-19 22:39

阅读量:2

有时数据的分类并不像我们想象的那么简单，需要高次曲线才能分类。

就像下面的数据：

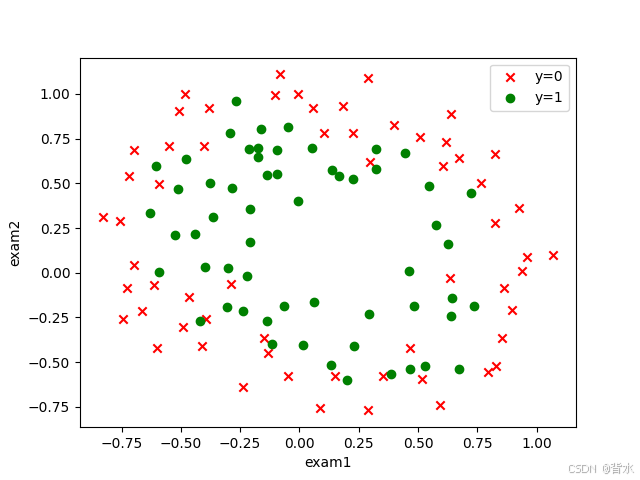
数据集最后给出：

我们这样看，至少需要达到2次以及以上的曲线才可以进行比较准确的分类。

比如如果已知数据有3列(两列特征)

x1	x2	y
-1	-1	1
0.5	0.5	0
0	1	1

那么我们的目标是

[
1,
x1,
x2,
x1*x2,
x1^2,
x2^2
]

现在的问题是如何将已经有的两列转化为这么6列？

我们可以按照以下推导：

$x_{1}^{0}x_{2}^{0} \\ x_{1}^{0}x_{2}^{1}\\ x_{1}^{0}x_{2}^{2}\\ x_{1}^{1}x_{2}^{0}\\ x_{1}^{1}x_{2}^{1}\\ x_{1}^{2}x_{2}^{0}$

def feature_mapping(x1, x2, power):     data = {}     for i in range(0, power + 1):         for j in range(power - i + 1):             data['f{}{}'.format(i,j)]=np.power(x1,i)*np.power(x2,j)     return pd.DataFrame(data)  x1=data['Exam1'] x2=data['Exam2']  data2=feature_mapping(x1,x2,2) print(data2.head())

f00 f01 f02 f10 f11 f20
0 1.0 0.69956 0.489384 0.051267 0.035864 0.002628
1 1.0 0.68494 0.469143 -0.092742 -0.063523 0.008601
2 1.0 0.69225 0.479210 -0.213710 -0.147941 0.045672
3 1.0 0.50219 0.252195 -0.375000 -0.188321 0.140625
4 1.0 0.46564 0.216821 -0.513250 -0.238990 0.263426

取数据集：

x1 = data['Exam1'] x2 = data['Exam2']  data2 = feature_mapping(x1, x2, 2) # print(data2.head())  X = data2.values print(X.shape) y = data['Accepted'].values.reshape((len(data.iloc[:,-1]), 1)) print(y.shape)

(118, 6)
(118, 1)

损失函数：

因为非线性的很容易进行过拟合，所以需要进行正则化。

那么什么是正则化呢？

我们先看一下最后得到的损失函数的形式

$J(\theta)=-\frac{1}{m}[y*log(\hat{y})+(1-y)*log(1-\hat{y})]+\frac{\lambda }{2m}\sum_{j=1}^{n}$

这里面的最后一项用来调节参数，防止出现过拟合和欠拟合。

注意这里的j是从1开始的，我们原来的X多加了一列1(索引为0)，这里从1开始的，没有计算哪个常数。

求导后：

for j==0:

$\frac{\partial J(\theta)}{\partial \theta_{j}}=\frac{1}{m}\sum_{i=1}^{m}(h_{\theta}(x^{(i)})-y^{(i)})x^{(i)}_{j}$

for j>=1:

$\frac{\partial J(\theta)}{\partial \theta_{j}}=\frac{1}{m}\sum_{i=1}^{m}(h_{\theta}(x^{(i)})-y^{(i)})x^{(i)}_{j}+\frac{\lambda }{m}\theta_{j}$

def sigmoid(z):     return 1.0 / (1 + np.exp(-z))   def cost_function(X, y, theta, lamba):     A = sigmoid(X @ theta)     first = y * np.log(A)     second = (1 - y) * np.log(1 - A)     reg = np.sum(np.power(theta[1:], 2)) * lamba / (2 * len(X))     return -np.sum(first + second) / len(X) + reg  theta = np.zeros((28,1)) lamda =1 cost_init = cost_function(X,y,theta,lamda) print(cost_init)

0.6931471805599454

梯度下降：

def gradientDescent(X, y, theta, alpha, iters, lamba):     costs = []     m = len(X)     reg = theta[1:] * lamba / m                #后面的惩罚项（防止过拟合）     reg = np.insert(reg, 0, values=0, axis=0)  #每次将常数置为0     for i in range(iters):         A = sigmoid(X @ theta)                 #预测值         theta = theta - alpha / m * (X.T @ (A - y) + reg)   #梯度下降         cost = cost_function(X, y, theta, lamba)            #损失函数         costs.append(cost)                      return costs, theta

预测：

alpha = 0.001 iters = 200000 lamba = 0.001 costs, theta = gradientDescent(X, y,theta,alpha,iters,lamba)  print("---------------------------") print(theta)  plt.figure() plt.plot(range(iters), costs, label='Cost') plt.xlabel('Iterations') plt.ylabel('Cost') plt.title('Cost Function Convergence') plt.legend() plt.show()   def predict(X,theta):     pre = sigmoid(X@theta)     return [1 if i >= 0.5 else 0 for i in pre ]   y_pre = predict(X,theta)  # 绘制真实值与预测值的比较图 plt.figure() plt.plot(range(len(y)), y, label='real_values', linestyle='-', marker='o', color='g') plt.plot(range(len(y)), y_pre, label='pre_value', linestyle='--', marker='x', color='r') plt.xlabel('label') plt.ylabel('value') plt.title('differ') plt.legend() plt.show()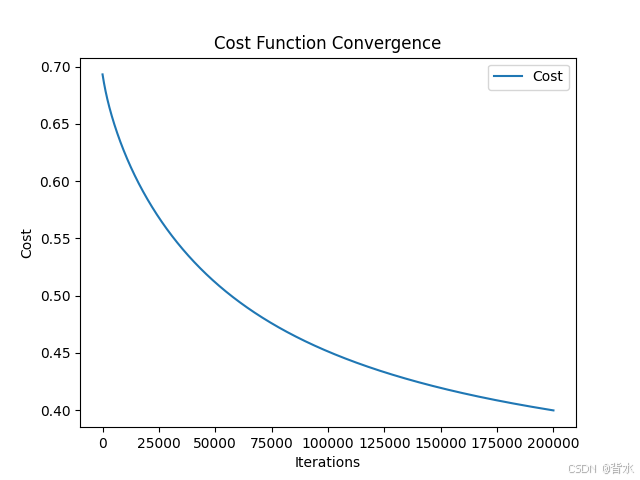

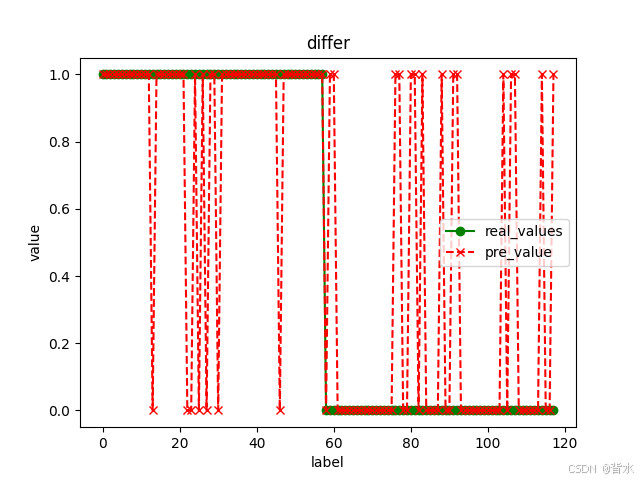
theta=[[ 1.87511207]
[ 2.023306 ]
[-2.13296198]
[-0.23971119]
[-1.94042125]
[-0.757585 ]
[-1.56403399]
[ 1.18536314]
[-1.68977623]
[-0.63345976]
[-0.53685159]
[-0.54677843]
[-0.29785185]
[-3.10618505]
[-0.67450464]
[-1.02252107]
[-0.48703712]
[-0.55736928]
[ 0.32233067]
[-0.14001433]
[-0.07578518]
[ 0.00558004]
[-2.37395054]
[-0.38709684]
[-0.49270366]
[-0.35696397]
[ 0.01562081]
[-1.74571902]]

整体代码：

import pandas as pd import numpy as np import matplotlib  matplotlib.use('tKAgg') import matplotlib.pyplot as plt  # 读取数据 path = "d:\\JD\\Documents\\大学等等等\\自学部分\\machine_-learning-master\\machine_-learning-master\\ex_2\\ex2data2.txt" data = pd.read_csv(path, names=['Exam1', 'Exam2', 'Accepted']) print(data.head())   # fig, ax = plt.subplots() # ax.scatter(data[data['Accepted'] == 0]['Exam1'], data[data['Accepted'] == 0]['Exam2'], c='r', marker='x', label='y=0') # ax.scatter(data[data['Accepted'] == 1]['Exam1'], data[data['Accepted'] == 1]['Exam2'], c='g', marker='o', label='y=1') # ax.legend() # ax.set( #     xlabel='exam1', #     ylabel='exam2' # ) # plt.show()  def feature_mapping(x1, x2, power):     data = {}     for i in range(0, power + 1):         for j in range(power - i + 1):             data['f{}{}'.format(i, j)] = np.power(x1, i) * np.power(x2, j)     return pd.DataFrame(data)   x1 = data['Exam1'] x2 = data['Exam2']  data2 = feature_mapping(x1, x2, 6) # print(data2.head())  X = data2.values print(X.shape) y = data['Accepted'].values.reshape((len(data.iloc[:, -1]), 1)) print(y.shape)   def sigmoid(z):     return 1.0 / (1 + np.exp(-z))   def cost_function(X, y, theta, lamba):     A = sigmoid(X @ theta)     first = y * np.log(A)     second = (1 - y) * np.log(1 - A)     reg = np.sum(np.power(theta[1:], 2)) * lamba / (2 * len(X))     return -np.sum(first + second) / len(X) + reg   theta = np.zeros((28, 1)) lamda = 1   # cost_init = cost_function(X,y,theta,lamda) # print(cost_init)  def gradientDescent(X, y, theta, alpha, iters, lamba):     costs = []     m = len(X)     reg = theta[1:] * lamba / m     reg = np.insert(reg, 0, values=0, axis=0)     for i in range(iters):         A = sigmoid(X @ theta)         theta = theta - alpha / m * (X.T @ (A - y) + reg)         cost = cost_function(X, y, theta, lamba)         costs.append(cost)     return costs, theta  alpha = 0.001 iters = 200000 lamba = 0.001 costs, theta = gradientDescent(X, y,theta,alpha,iters,lamba)  print("---------------------------") print(theta)  plt.figure() plt.plot(range(iters), costs, label='Cost') plt.xlabel('Iterations') plt.ylabel('Cost') plt.title('Cost Function Convergence') plt.legend() plt.show()   def predict(X,theta):     pre = sigmoid(X@theta)     return [1 if i >= 0.5 else 0 for i in pre ]   y_pre = predict(X,theta)  # 绘制真实值与预测值的比较图 plt.figure() plt.plot(range(len(y)), y, label='real_values', linestyle='-', marker='o', color='g') plt.plot(range(len(y)), y_pre, label='pre_value', linestyle='--', marker='x', color='r') plt.xlabel('label') plt.ylabel('value') plt.title('differ') plt.legend() plt.show()

附件：

数据集

0.051267,0.69956,1
-0.092742,0.68494,1
-0.21371,0.69225,1
-0.375,0.50219,1
-0.51325,0.46564,1
-0.52477,0.2098,1
-0.39804,0.034357,1
-0.30588,-0.19225,1
0.016705,-0.40424,1
0.13191,-0.51389,1
0.38537,-0.56506,1
0.52938,-0.5212,1
0.63882,-0.24342,1
0.73675,-0.18494,1
0.54666,0.48757,1
0.322,0.5826,1
0.16647,0.53874,1
-0.046659,0.81652,1
-0.17339,0.69956,1
-0.47869,0.63377,1
-0.60541,0.59722,1
-0.62846,0.33406,1
-0.59389,0.005117,1
-0.42108,-0.27266,1
-0.11578,-0.39693,1
0.20104,-0.60161,1
0.46601,-0.53582,1
0.67339,-0.53582,1
-0.13882,0.54605,1
-0.29435,0.77997,1
-0.26555,0.96272,1
-0.16187,0.8019,1
-0.17339,0.64839,1
-0.28283,0.47295,1
-0.36348,0.31213,1
-0.30012,0.027047,1
-0.23675,-0.21418,1
-0.06394,-0.18494,1
0.062788,-0.16301,1
0.22984,-0.41155,1
0.2932,-0.2288,1
0.48329,-0.18494,1
0.64459,-0.14108,1
0.46025,0.012427,1
0.6273,0.15863,1
0.57546,0.26827,1
0.72523,0.44371,1
0.22408,0.52412,1
0.44297,0.67032,1
0.322,0.69225,1
0.13767,0.57529,1
-0.0063364,0.39985,1
-0.092742,0.55336,1
-0.20795,0.35599,1
-0.20795,0.17325,1
-0.43836,0.21711,1
-0.21947,-0.016813,1
-0.13882,-0.27266,1
0.18376,0.93348,0
0.22408,0.77997,0
0.29896,0.61915,0
0.50634,0.75804,0
0.61578,0.7288,0
0.60426,0.59722,0
0.76555,0.50219,0
0.92684,0.3633,0
0.82316,0.27558,0
0.96141,0.085526,0
0.93836,0.012427,0
0.86348,-0.082602,0
0.89804,-0.20687,0
0.85196,-0.36769,0
0.82892,-0.5212,0
0.79435,-0.55775,0
0.59274,-0.7405,0
0.51786,-0.5943,0
0.46601,-0.41886,0
0.35081,-0.57968,0
0.28744,-0.76974,0
0.085829,-0.75512,0
0.14919,-0.57968,0
-0.13306,-0.4481,0
-0.40956,-0.41155,0
-0.39228,-0.25804,0
-0.74366,-0.25804,0
-0.69758,0.041667,0
-0.75518,0.2902,0
-0.69758,0.68494,0
-0.4038,0.70687,0
-0.38076,0.91886,0
-0.50749,0.90424,0
-0.54781,0.70687,0
0.10311,0.77997,0
0.057028,0.91886,0
-0.10426,0.99196,0
-0.081221,1.1089,0
0.28744,1.087,0
0.39689,0.82383,0
0.63882,0.88962,0
0.82316,0.66301,0
0.67339,0.64108,0
1.0709,0.10015,0
-0.046659,-0.57968,0
-0.23675,-0.63816,0
-0.15035,-0.36769,0
-0.49021,-0.3019,0
-0.46717,-0.13377,0
-0.28859,-0.060673,0
-0.61118,-0.067982,0
-0.66302,-0.21418,0
-0.59965,-0.41886,0
-0.72638,-0.082602,0
-0.83007,0.31213,0
-0.72062,0.53874,0
-0.59389,0.49488,0
-0.48445,0.99927,0
-0.0063364,0.99927,0
0.63265,-0.030612,0

支持

资讯

特征映射(机器学习)

相关阅读

广告一刻