Python 水文预报三水源新安江模型构建
1 前言
新安江模型是极为重要的水文模型,此拙作只作为简单的引导,希望大家在阅读的时候能够有自己的思考,例如引入智能进化算法率定参数、程序自动绘制精美的图表、程序自动输出评价指标、分析模型对参数的敏感程序、思考模型产生误差的原因、实现改进的新安江模型、提升自己的编程能力。
2 新安江模型介绍
新安江模型是华东水利学院(现河海大学)赵人俊教授团队提出的一个水文模型,是中国少有的一个具有世界影响力的水文模型。新安江模型模型适用于湿润地区和半湿润地区。它将整个流域划分为多个块状单元流域,并对每个单元流域进行产汇流计算,得出单元流域的出口流量过程。接着进行河道洪水演算,求得流域出口的流量过程。将每个单元流域的出流过程相加,即可得到流域的总出流过程。
2.1 模型结构
为了考虑降水和流域下垫面分布不均匀的影响,新安江模型的结构设计为分散性的,分为蒸散发计算、产流计算、分水源计算和汇流计算四个层次结构。每块单元流域的计算流程如下图所示。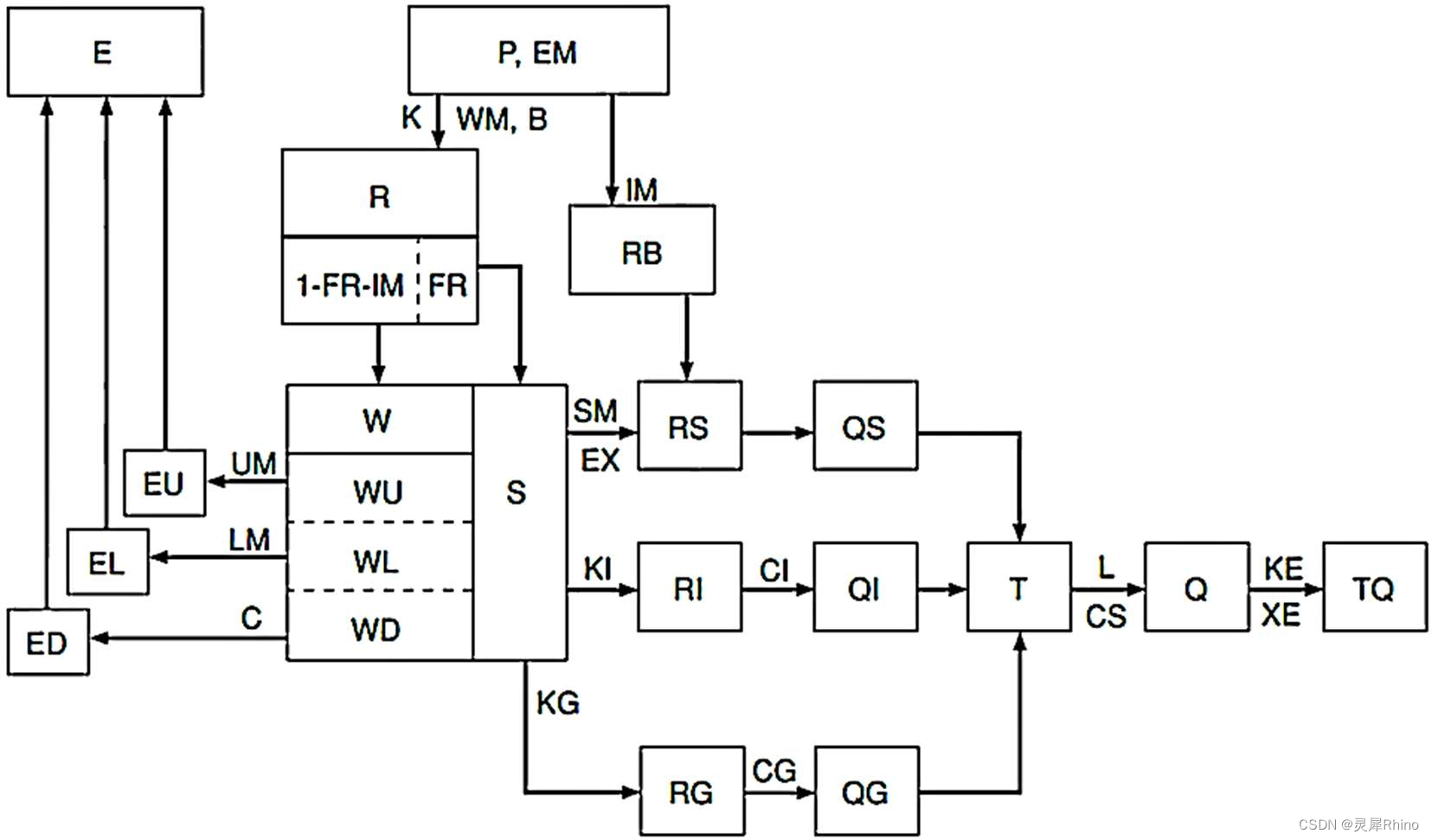
2.1.1 蒸散发计算
在新安江模型中,流域蒸散发计算没有考虑流域内土壤含水量在面上分布的不均匀性,而是按土壤垂向分布的不均匀性将土层分为三层,用三层蒸散发模型计算蒸散发量,计算公式如下:
2.1.2 产流计算
产流计算采用蓄满产流机制。蓄满是指包气带的土壤含水量达到田间持水量。蓄满产流是指:降水在满足田间持水量以前不产流,所有的降水都被土壤所吸收而成为张力水;降水在满足田间持水量以后,所有的降水扣除蒸发量都产流。
按照蓄满产流的概念,采用蓄水容量-面积分配曲线来考虑土壤缺水量分布不均匀的问题,以此来计算产流量 R。
- 计算流域平均的初始土壤含水量对应的纵坐标 a:

- 如果 P - E > 0 ,计算径流量 R:
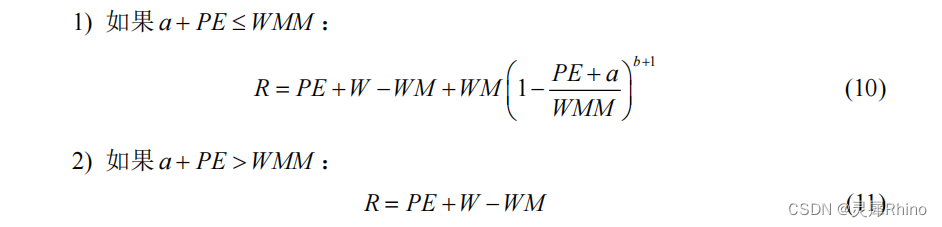
2.1.3 三水源划分
根据径流实验观测和径流形成原理,将径流划分为地面径流 RS、壤中流 RI、地下径流 RG。与蓄满产流模型相类似,由于下垫面的不均匀性,自由水蓄量也存在空间分布不均匀性,因此用自由水蓄水容量曲线来考虑这点,以此来进行三水源划分。
- 计算流域平均的初始自由水蓄量对应的纵坐标 AU:

- 计算地面径流 RS:

- 本时段的自由水蓄量 S:
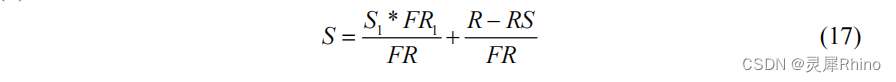
- 相应的壤中流 RI 和地下径流 RG:
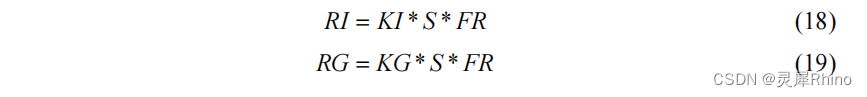

- 下一时段初的自由水蓄量 S1:
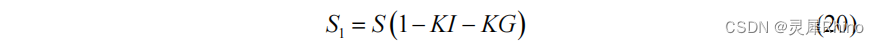
2.1.4 三水源汇流计算
- 地表径流汇流,采用线性水库法:

- 壤中流汇流,表层自由水侧向流动,出流后成为表层壤中流进入河网。若土层较厚,表层自由水还可以渗入到深层土,经过深层土的调蓄作用才进入河网。壤中流汇流也可采用线性水库法:

- 地下径流汇流,采用线性水库法:

- 单元面积河网总入流,单元面积河网总入流 QT 为地表径流量、壤中流与地下径流量之和:
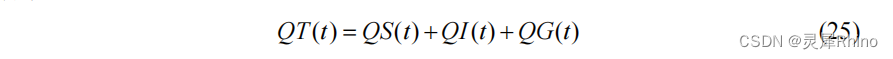
- 单元面积河网汇流,单位面积的河流采用滞后演算法:

- 河道汇流,河道汇流采用马斯京根分段流量演算法,将演算河段分为 n 个单元河段,用马斯京根法连续进行 n 次演算,以求得出流过程:

2.2 模型参数
新安江模型中各参数意义如下(还包括初始土壤含水量):
| 参数 | 参数物理意义 |
|---|---|
| K | 蒸散发折算系数 |
| B | 流域蓄水容量分布曲线指数 |
| C | 深层散发系数 |
| WM | 张力水容量 |
| WUM | 上层张力水容量 |
| WLM | 下层张力水容量 |
| IM | 不透水面积比例 |
| SM | 自由水容量 |
| EX | 流域自由水容量分布曲线指数 |
| KG | 地下水出流系数 |
| KI | 壤中流出流系数 |
| CG | 地下水消退系数 |
| CI | 壤中流消退系数 |
| CS | 河网水流消退系数 |
| L | 河网汇流滞时 |
| X | 马斯京根法参数 |
3 模型代码
新安江模型有两种时间尺度:日模型(24 h)、次洪模型(1 h)。
日模型的结果可为次洪模型提供初始值,这里只给出次洪模型相应阶段的代码。如果汇流时间小于24 h,日模型可以简化不考虑河道汇流。
3.1 代码说明
参考:Python 建立流域三层蒸发和蓄满产流模型(二水源划分)
需要用到pandas库和math库,不会的自行CSDN。
3.2 更新土壤含水量
初次计算需要设置初始土壤含水量,后每次计算需要先更新土壤含水量。
def calculate_WU_WL_WD(df, i): # 更新土壤含水量 if i == 0: # 设置初始值 df.loc[i, ["WU"]] = WUM_init df.loc[i, ["WL"]] = WLM_init df.loc[i, ["WD"]] = WDM_init else: infi = df["PE"][i - 1] - df["R"][i - 1] # 上层蓄水量不为0,则只存在EU;且上层蓄水量与下渗的净降雨有关 df.loc[i, ["WU"]] = df["WU"][i - 1] + infi df.loc[i, ["WL"]] = df["WL"][i - 1] # 假设扣除损失量后上层蓄水量仍大于或等于0,则中、深层蓄水量不会变化 df.loc[i, ["WD"]] = df["WD"][i - 1] if df["WU"][i] < 0: # 若上层蓄水量小于损失量 df.loc[i, ["WL"]] = df["WL"][i - 1] + df["WU"][i] # 则蒸发损失认为发生中层 df.loc[i, ["WU"]] = 0 df.loc[i, ["WD"]] = df["WD"][i - 1] # 假设扣除损失量后中层蓄水量仍大于或等于0,则深层蓄水量不会变化 if df["WL"][i] < 0: # 若中层蓄水量小于损失量 df.loc[i, ["WD"]] = df["WD"][i - 1] + df["WL"][i] # 则蒸发损失认为发生深层 df.loc[i, ["WL"]] = 0 df.loc[i, ["WU"]] = 0 if df["WD"][i] < 0: # 若深层蓄水量小于损失量 df.loc[i, ["WD"]] = 0 df.loc[i, ["WL"]] = 0 df.loc[i, ["WU"]] = 0 # 设置蓄水量上限,不应超过蓄水容量 if df["WU"][i] > WUM: # 若扣除损失后入渗量足以补充上层蓄水容量,则多余的会逐层向下补充 df.loc[i, ["WL"]] = df["WU"][i] - WUM + df["WL"][i - 1] # 首先补充中层 df.loc[i, ["WU"]] = WUM df.loc[i, ["WD"]] = df["WD"][i - 1] if df["WL"][i] > WLM: # 若扣除损失后入渗量足以补充中层蓄水容量,则多余的会逐层向下补充 df.loc[i, ["WD"]] = df["WL"][i] - WLM + df["WD"][i - 1] # 补充深层 df.loc[i, ["WU"]] = WUM df.loc[i, ["WL"]] = WLM if df["WD"][i] > WDM: # 完全补充 df.loc[i, ["WD"]] = WDM df.loc[i, ["WU"]] = WUM df.loc[i, ["WL"]] = WLM 3.3 三层蒸发模型计算
四个条件判断,需要先计算流域蒸发能力。
def calculate_EU_EL_ED(df, i): # 三层蒸发模型计算 df.loc[i, ["EP"]] = df["E0"][i] * K # 计算流域蒸发能力 """四个条件判断""" if df["WU"][i] + df["P"][i] >= df["EP"][i]: df.loc[i, ["EU"]] = df["EP"][i] df.loc[i, ["EL"]] = 0 df.loc[i, ["ED"]] = 0 if df["WU"][i] + df["P"][i] < df["EP"][i] and df["WL"][i] >= C * WLM: df.loc[i, ["EU"]] = df["WU"][i] + df["P"][i] df.loc[i, ["EL"]] = (df["EP"][i] - df["EU"][i]) * (df["WL"][i] / WLM) df.loc[i, ["ED"]] = 0 if df["WU"][i] + df["P"][i] < df["EP"][i] and C * (df["EP"][i] - df["EU"][i]) <= df["WL"][i] and df["WL"][ i] < C * WLM: df.loc[i, ["EU"]] = df["WU"][i] + df["P"][i] df.loc[i, ["EL"]] = C * (df["EP"][i] - df["EU"][i]) df.loc[i, ["ED"]] = 0 if df["WU"][i] + df["P"][i] < df["EP"][i] and df["WL"][i] < C * (df["EP"][i] - df["EU"][i]): df.loc[i, ["EU"]] = df["WU"][i] + df["P"][i] df.loc[i, ["EL"]] = df["WL"][i] df.loc[i, ["ED"]] = C * (df["EP"][i] - df["EU"][i]) - df["EL"][i] 3.4 蒸发量、净降水量、土壤总蓄水量计算
需要计算蒸发量E、净降水量PE、土壤总蓄水量计算W,为后续计算产流量R做准备。
def calculate_E_PE_W(df, i): df.loc[i, ["E"]] = df["EU"][i] + df["EL"][i] + df["ED"][i] # 计算总的蒸发量 df.loc[i, ["PE"]] = df["P"][i] - df["E"][i] # 计算降水扣除蒸发量 df.loc[i, ["W"]] = df["WU"][i] + df["WL"][i] + df["WD"][i] # 计算土壤总蓄水量 3.5 蓄满产流模型计算产流
采用蓄满产流模型,认为当PE > 0时才有可能产生径流R,否则不产生。
def calculate_R(df, i): # 蓄满产流模型计算产流 """计算公式""" if df["PE"][i] > 0: # PE>0才有可能产生径流 a = WMM * (1 - math.pow((1 - df["W"][i] / WM), (1 / (1 + b)))) if a + df["PE"][i] <= WMM: df.loc[i, ["R"]] = df["PE"][i] + df["W"][i] - WM + WM * math.pow((1 - (df["PE"][i] + a) / WMM), (b + 1)) else: df.loc[i, ["R"]] = df["PE"][i] - (WM - df["W"][i]) else: df.loc[i, ["R"]] = 0 3.6 流域产流面积计算
根据蓄水容量-面积分配曲线计算流域产流面积。
def calculate_FR(df, i): # 计算流域产流面积 """三水源划分产流面积迭代""" if df["R"][i] > 0: df.loc[i, "FR"] = df["R"][i] / df["PE"][i] if df["FR"][i] > 1: df.loc[i, "FR"] = 1 else: if i == 0: df.loc[i, "FR"] = FR1 else: df.loc[i, "FR"] = df["FR"][i - 1] 3.7 三水源划分
将产流R划分为RS、RG、RI,可参照三水源划分公式,首个时段设置初始的自由水蓄量。
def calculate_RS_RG_RI(df, i): # 三水源划分判断函数 """计算公式""" if i == 0: # 第一时段计算 df.loc[i, "S1"] = S1 if df["PE"][i] > 0: AU = SMM * (1 - math.pow((1 - (((df["S1"][i] * FR1) / df["FR"][i]) / Sm)), 1 / (1 + EX))) if df["PE"][i] + AU < SMM: df.loc[i, "RS"] = df["FR"][i] * (df["PE"][i] + (df["S1"][i] * FR1) / df["FR"][i] - Sm + Sm * math.pow((1 - (df["PE"][i] + AU) / SMM), 1 + EX)) if df["PE"][i] + AU >= SMM: df.loc[i, "RS"] = df["FR"][i] * (df["PE"][i] + (df["S1"][i] * FR1) / df["FR"][i] - Sm) S = (df["S1"][i] * FR1) / df["FR"][i] + (df["R"][i] - df["RS"][i]) / df["FR"][i] df.loc[i, "RI"] = KI * S * df["FR"][i] df.loc[i, "RG"] = KG * S * df["FR"][i] df.loc[i + 1, "S1"] = S * (1 - KI - KG) else: S = (df["S1"][i] * FR1) / df["FR"][i] df.loc[i + 1, "S1"] = S * (1 - KG - KI) df.loc[i, "RS"] = 0 df.loc[i, "RG"] = KI * S * df["FR"][i] df.loc[i, "RI"] = KG * S * df["FR"][i] else: # 其余时段计算 if df["PE"][i] > 0: AU = SMM * (1 - math.pow((1 - (((df["S1"][i] * df["FR"][i - 1]) / df["FR"][i]) / Sm)), 1 / (1 + EX))) if df["PE"][i] + AU < SMM: df.loc[i, "RS"] = df["FR"][i] * ( df["PE"][i] + (df["S1"][i] * df["FR"][i - 1]) / df["FR"][i] - Sm + Sm * math.pow((1 - (df["PE"][i] + AU) / SMM), 1 + EX)) if df["PE"][i] + AU >= SMM: df.loc[i, "RS"] = df["FR"][i] * ( df.loc[i, "PE"] + (df["S1"][i] * df["FR"][i - 1]) / df["FR"][i] - Sm) S = (df["S1"][i] * df["FR"][i - 1]) / df["FR"][i] + (df["R"][i] - df["RS"][i]) / df["FR"][i] df.loc[i, "RI"] = KI * S * df["FR"][i] df.loc[i, "RG"] = KG * S * df["FR"][i] df.loc[i + 1, "S1"] = S * (1 - KI - KG) else: S = (df["S1"][i] * df["FR"][i - 1]) / df["FR"][i] df.loc[i + 1, "S1"] = S * (1 - KG - KI) df.loc[i, "RS"] = 0 df.loc[i, "RG"] = KG * S * df["FR"][i] df.loc[i, "RI"] = KI * S * df["FR"][i] 3.8 三水源汇流计算
根据线性水库、滞后演算公式,对RS、RG、RI三种径流成分进行汇流计算。
def calculate_Q(df, i, U): # 三水源汇流计算,单元面积河网汇流 """计算公式""" df.loc[i, "QS"] = df["RS"][i] * U # 地面径流的坡地汇流 if i == 0: # 设置初始壤中流、地下径流 df.loc[i, "QI"] = 1 / 3 * Q df.loc[i, "QG"] = 1 / 3 * Q else: df.loc[i, "QI"] = CI * df["QI"][i - 1] + (1 - CI) * df["RI"][i] * U # 壤中流汇流,消退系数CI df.loc[i, "QG"] = CG * df["QG"][i - 1] + (1 - CG) * df["RG"][i] * U # 地下径流汇流,消退系数CG df.loc[i, "QT"] = df["QS"][i] + df["QI"][i] + df["QG"][i] # 单元面积河网汇流,滞后演算法 if 0 <= i <= L: df.loc[i, "Qt"] = Q elif i > L: df.loc[i, "Qt"] = df["Qt"][i - 1] * CS + (1 - CS) * df["QT"][i - L] 3.9 河道汇流演算
采用马斯京根法进行河道汇流演算,需要提前计算好子河段数量n。
def calculate_Qi(df, i, n): # 河道汇流演算,马斯京根法 df.loc[i, "Q1"] = df["Qt"][i] if n > 0: """单元河段参数""" K_l = T x_l = 0.5 - n * (1 - 2 * X) / 2 """计算C0、C1、C2""" C0 = (0.5 * T - K_l * x_l) / (0.5 * T + K_l - K_l * x_l) C1 = (0.5 * T + K_l * x_l) / (0.5 * T + K_l - K_l * x_l) C2 = 1 - C0 - C1 # df.loc[i, "Q1"] = df["Qt"][i] for p in range(n): """进行分段计算""" I2 = df[f"Q{1 + p}"][i] if i == 0: I1 = Q Q1 = Q else: I1 = df[f"Q{1 + p}"][i - 1] Q1 = df[f"Q{2 + p}"][i - 1] df.loc[i, f"Q{2 + p}"] = C0 * I2 + C1 * I1 + C2 * Q1 3.10 计算顺序
需要注意的是,这里是对每个子流域分别(循环)计算,每个sheet表对应一个子流域的降水,最后需要加在一起才是流域出口断面流量。
if __name__ == '__main__': ... 忽略数据读取代码和保存至excel代码 ... for k in range(sheet_count): print(f"第{k + 1}次运行ing") df = read_data(k) # 这个是自编的函数 for i in range(len(df)): # 循环 calculate_WU_WL_WD(df, i) calculate_EU_EL_ED(df, i) calculate_E_PE_W(df, i) calculate_R(df, i) calculate_FR(df, i) calculate_RS_RG_RI(df, i) U = Area[k] / (3.6 * T) # F单位为km^2,T单位为h calculate_Q(df, i, U) calculate_Qi(df, i, N[k]) ... 忽略保存至excel代码 ... 这里没有给出完整的读取数据、处理数据、绘制图表代码,需要根据自己的数据来写,不断思考和寻找问题答案的过程才是编程!。
以下是用于计算的Excel格式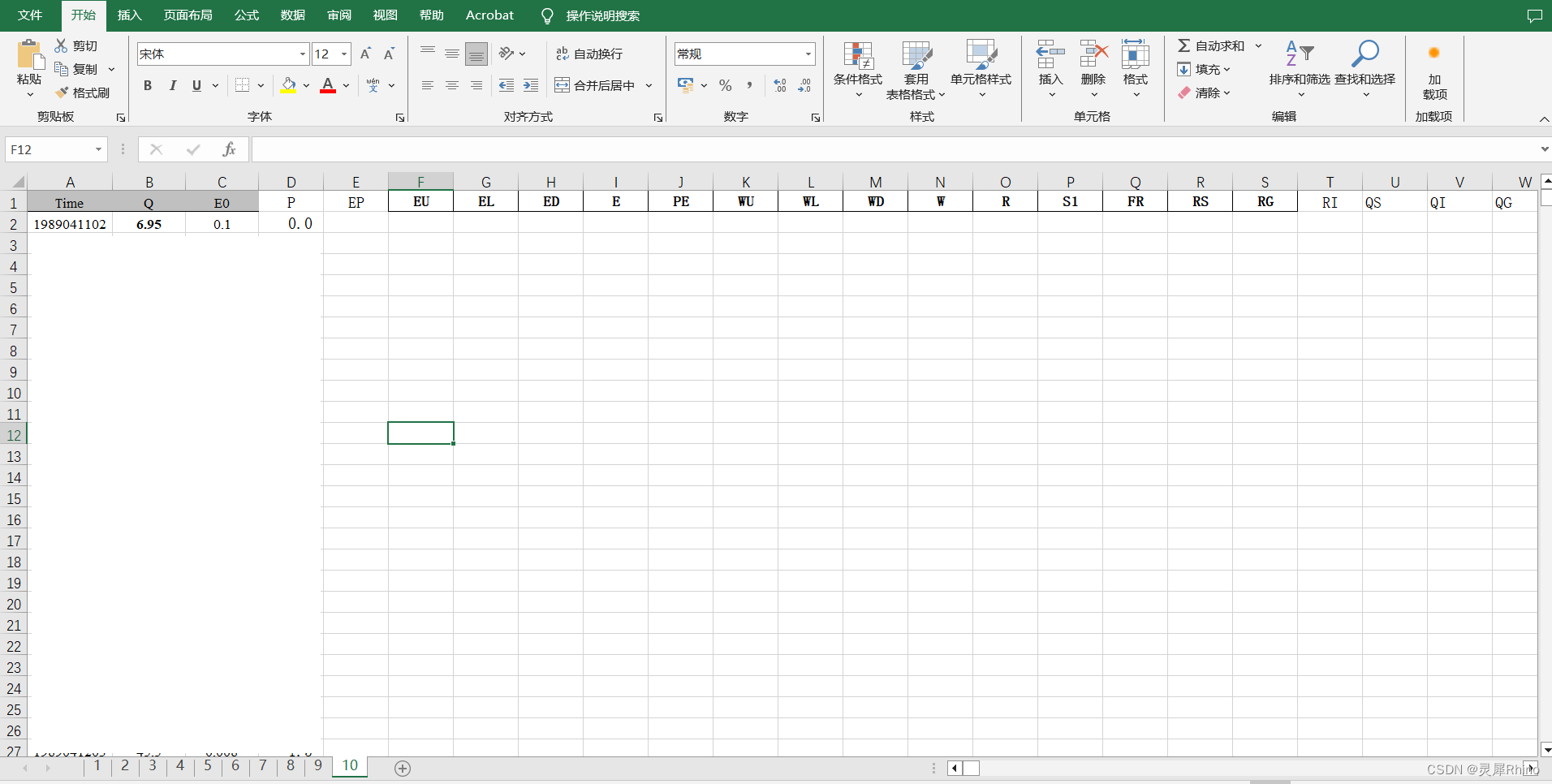
4 总结
新安江模型是极为重要的水文模型,此拙作只作为简单的引导,希望大家在阅读的时候能够有自己的思考。
如有问题,欢迎探讨,邮箱:mymail_zo@qq.com
