阅读量:2
射线和平面求交
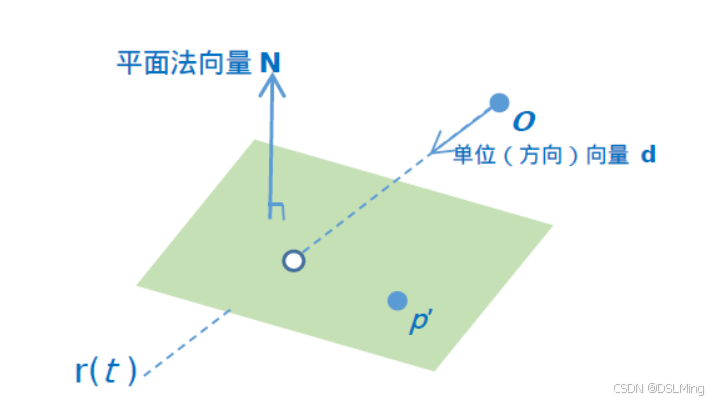
1、平面方程
如果已知平面的高度(即沿法向量方向的距离)为 height,平面方程可以表示为:
n ^ ⋅ p = h e i g h t \bold{\hat{n}} \cdot p = height n^⋅p=height
p p p 是平面上的任意一点
height 的正负取决于法向量的方向。
2、射线参数方程
r ( t ) = p 0 + t ⋅ d i r \bold{r}(t) = p_0 + t \cdot \bold{dir} r(t)=p0+t⋅dir
p 0 p_0 p0: 是射线的起点
d i r dir dir: 是射线的方向向量
t t t: 表示沿着方向向量走的距离
3、计算交点
n ^ ⋅ ( p 0 + t ⋅ d i r ) = h e i g h t \bold{\hat{n}} \cdot (p_0 + t \cdot \bold{dir}) = height n^⋅(p0+t⋅dir)=height
展开后:
n ^ ⋅ p 0 + t ⋅ ( n ^ ⋅ d i r ) = h e i g h t \bold{\hat{n}} \cdot p_0 + t \cdot (\bold{\hat{n}} \cdot \bold{dir}) = height n^⋅p0+t⋅(n^⋅dir)=height
解这个方程,求出 t t t:
t = h e i g h t − n ^ ⋅ p 0 n ^ ⋅ d i r t = \frac{height - \bold{\hat{n}} \cdot p_0}{\bold{\hat{n}} \cdot \bold{dir}} t=n^⋅dirheight−n^⋅p0
4、代码实现
/** * 计算射线和平面的交点 * @param source 射线起点 * @param dir 射线方向 * @param normal 平面法向量 * @param height 平面高度 */ vec3 interceptPlane(in vec3 source, in vec3 dir, in vec3 normal, float height) { float distance = (-height - dot(normal, source)) / dot(normal, dir); if (distance > 0.0) return source + dir * distance; else return vec3(infinity); // 返回一个表示无穷远的向量 } 