鱼书全称《深度学习入门:基于Python的理论与实现》

1 NumPy 库
导入 NumPy 库,以后可以以 “np” 来调用
import numpy as np1.1 np.array()
np.array() 接收 Python 的列表作为参数,生成 NumPy 数组(numpy.ndarray)
python 的列表用中括号:
如 [2,3,4]
import numpy as np array = [1, 7, 3, 5] x = np.array(array) print(x) print(type(x))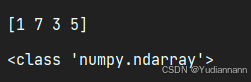
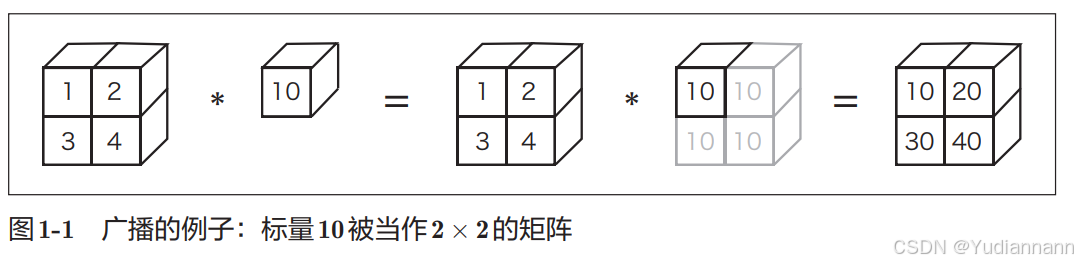
1.2 广播运算
基础运算:

广播运算:
方便了不同形状的数组进行计算
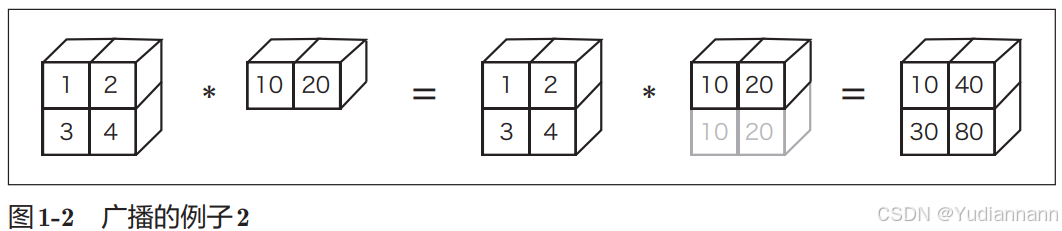
import numpy as np x = np.array([2, 7, 3, 5]) y = np.array([[2], [1]]) print(x+y)
注:x+y 和 y+x 结果一样
1.3 N 维矩阵
import numpy as np x = np.array([[2, 7, 3, 5], [1, 2, 3, 7], [8, 7, 5, 2]]) print(x) print(x.shape) 
矩阵可以进行运算
也是广播运算
import numpy as np x = np.array([[3, 5]]) y = np.array([[1], [2]]) print(x) print(y) print("\n") print(x + y) 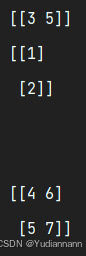
乘法(是直接对应元素的相乘)
import numpy as np x = np.array([[3, 5],[2,3]]) y = np.array([[1,2],[7,8]]) print(x) print(y) print("\n") print(x * y) 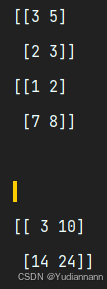
np.array可以生成一维数组。二维数组、三维数组等任意维数的数组。数学上将一维数组称为向量,将二维数组称为矩阵。另外,可以将一般化之后的向量或矩阵等统称为张量(tensor)。本书基本上将二维数组称为“矩阵”,将三维数组及三维以上的数组称为“张量”或“多维数组”
即:多维数组就是张量
1.4 访问元素
import numpy as np x = np.array([[3, 5], [2, 8]]) print(x[0]) # 访问一行 print(x[1][1]) # 访问一个元素 # for 遍历 for i in range(2): for j in range(2): print(x[i][j], end=" ") print("\n") flatX = x.flatten(); # 转为向量 print(flatX[np.array([0, 2, 3])]) # NumPy 的高级索引 print(x > 2) # 从 x 中抽出大于 15 的元素 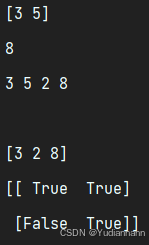
高级索引机制:
当使用一个数组作为索引时,NumPy 会将这个数组中的每个元素视为主数组中相应位置的索引
NumPy 中,主要的处理通过 C 或 C++ 实现的
2 Matplotlib 库
使用 pyplot 包
plt 方法:
import numpy as np import matplotlib.pyplot as plt x = np.arange(0, 6, 0.1) # 以0.1为单位,生成 0到 6的数据 y = np.sin(x) plt.plot(x,y) plt.show() 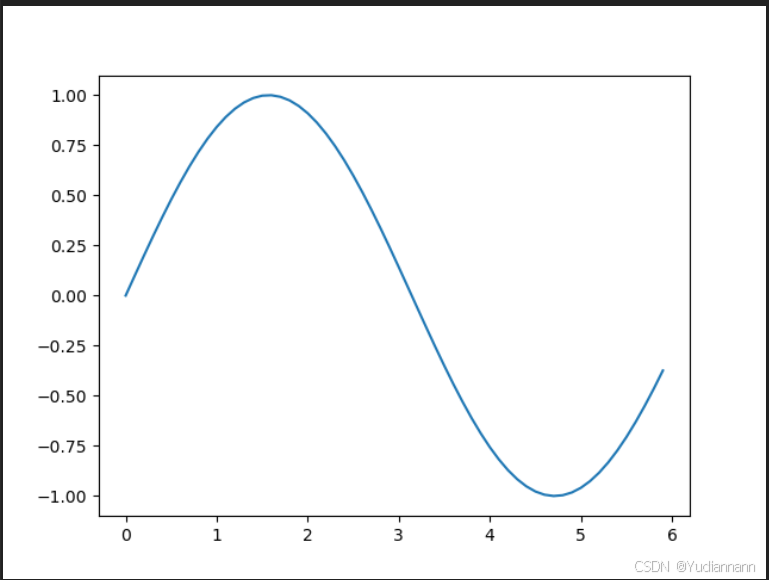
现在变得更复杂
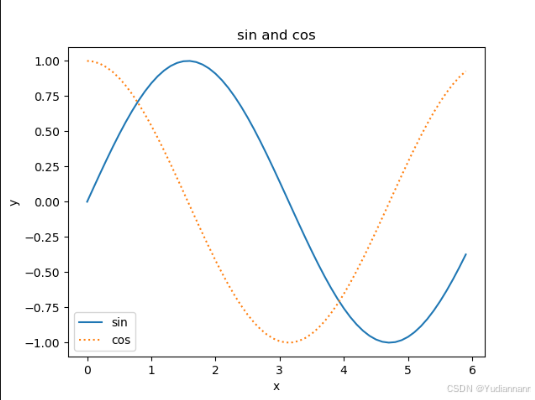
import numpy as np import matplotlib.pyplot as plt x = np.arange(0, 6, 0.1) # 以0.1为单位,生成 0到 6的数据 y1 = np.sin(x) y2 = np.cos(x) plt.plot(x, y1, label="sin") # 图例 plt.plot(x, y2, linestyle=":", label="cos") plt.xlabel("x") # 横轴标签 plt.ylabel("y") # 纵轴标签 plt.title("sin and cos") # 图标标题 plt.legend() # 显示图例 plt.show() # 展示图像 linestyle 的几种取值:
-实线(默认样式)--虚线-.点划线:点线'-'实线(与-相同,单引号在某些情况下用于确保字符串格式正确)'--'虚线(与--相同)'-.'点划线(与-.相同)':'点线(与:相同)''或'None'无线条,常用于标记或特殊用途
3 感知机
感知机是作为神经网络(深度学习)的起源的算法
感知机(Perceptron)是最早的一种人工神经网络模型,由 Frank Rosenblatt 在1957年提出。它是一种简单的线性二分类模型,用于模拟基础的神经元功能。感知机模型主要用于解决分类问题,特别是二元分类问题
感知机接收多个输入信号,输出一个信号
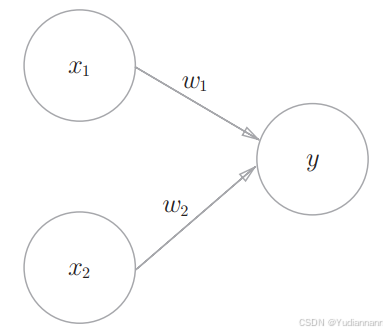
这是一个有两个输入的感知机,x1 和 x2 是输入,w1 和 w2 是权重
输入信号被送往神经元时,会被分别乘以固定的权重(w1x1、 w2x2)。神经元会计算传送过来的信号的总和,只有当这个总和超过了某个界限值时,才会输出1。这也称为“神经元被激活” 。这里将这个界限值称为阈值,用符号 θ 表示
数学表达:
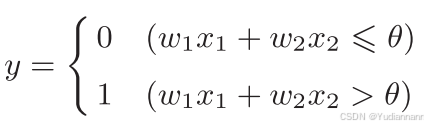
比如一个与门(当输出都为 1 时才输出 1 ):
设置参数
w1 = 0.5
w2 = 0.5
θ = 0.7
1、x1 = 0,x2 = 0,temp = w1x1 + w2x2 = 0,temp < θ,y = 0
2、x1 = 1,x2 = 0,temp = w1x1 + w2x2 = 0.5,temp < θ,y = 0
3、x1 = 0,x2 = 1,temp = w1x1 + w2x2 = 0.5,temp < θ,y = 0
4、x1 = 1,x2 = 1,temp = w1x1 + w2x2 = 1,temp > θ,y = 1
事实上对于与门有无数种设置参数的方法
决定感知机参数的并不是计算机,而是人。我们看着真值表这种“训练数据”,人工考虑(想到)了参数的值。而机器学习的课题就是将这个决定参数值的工作交由计算机自动进行
学习是确定合适的参数的过程,而人要做的是思考感知机的构造(模型),并把训练数据交给计算机
3.1 感知机的实现
3.1.1 简单实现
以与门为例:
def AND(x1, x2): w1, w2, theta = 0.5, 0.5, 0.7 temp = w1 * x1 + w2 * x2 if temp <= theta: return 0 else: return 1 print(AND(0, 0)) print(AND(0, 1)) print(AND(1, 0)) print(AND(1, 1)) ![]()
3.1.2 引入偏置
把 θ 换成 -b :
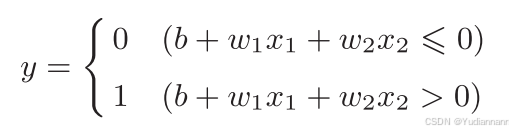
其中,b 为偏置
下面使用 numpy 实现
import numpy as np def AND(x1, x2): x = np.array([x1, x2]) w = np.array([0.5, 0.5]) # 权重 b = np.array([-0.7]) # 偏置 temp = np.sum(w * x) + b if temp > 0: return 1 else: return 0 print(AND(0, 0)) print(AND(0, 1)) print(AND(1, 0)) print(AND(1, 1)) 结果与上面相同
3.2 感知机的局限
可以用相同的方法实现与非门、或门,只需要改变权重和偏置即可
对于或门:
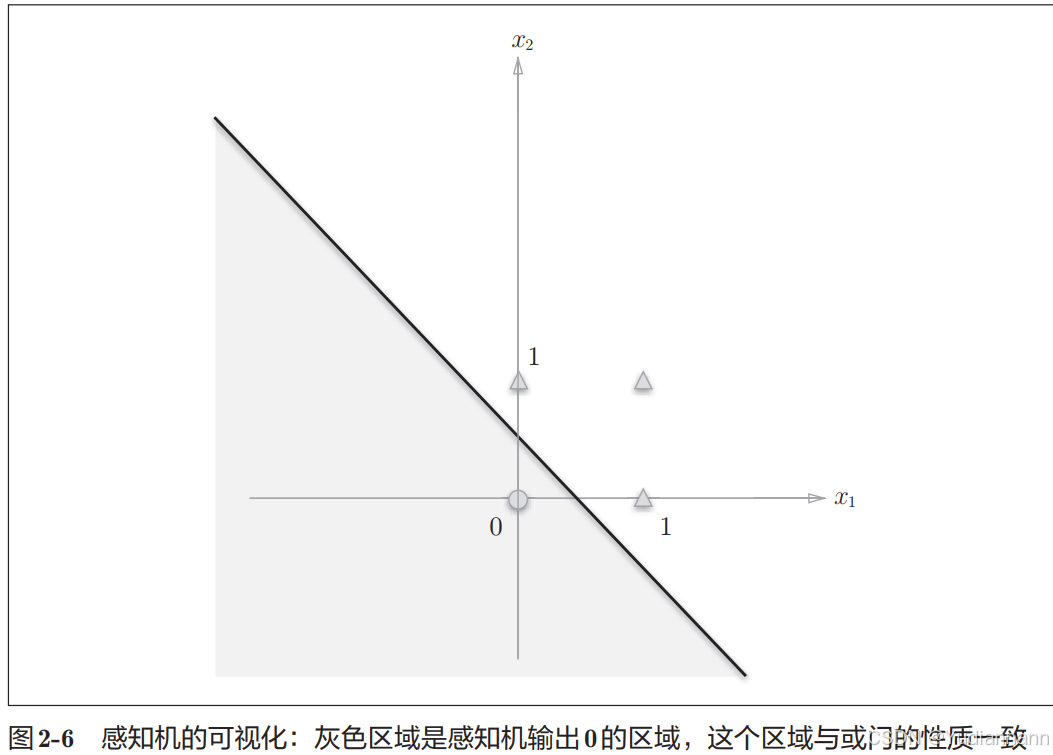
可以用一条直线进行分类
对于异或门
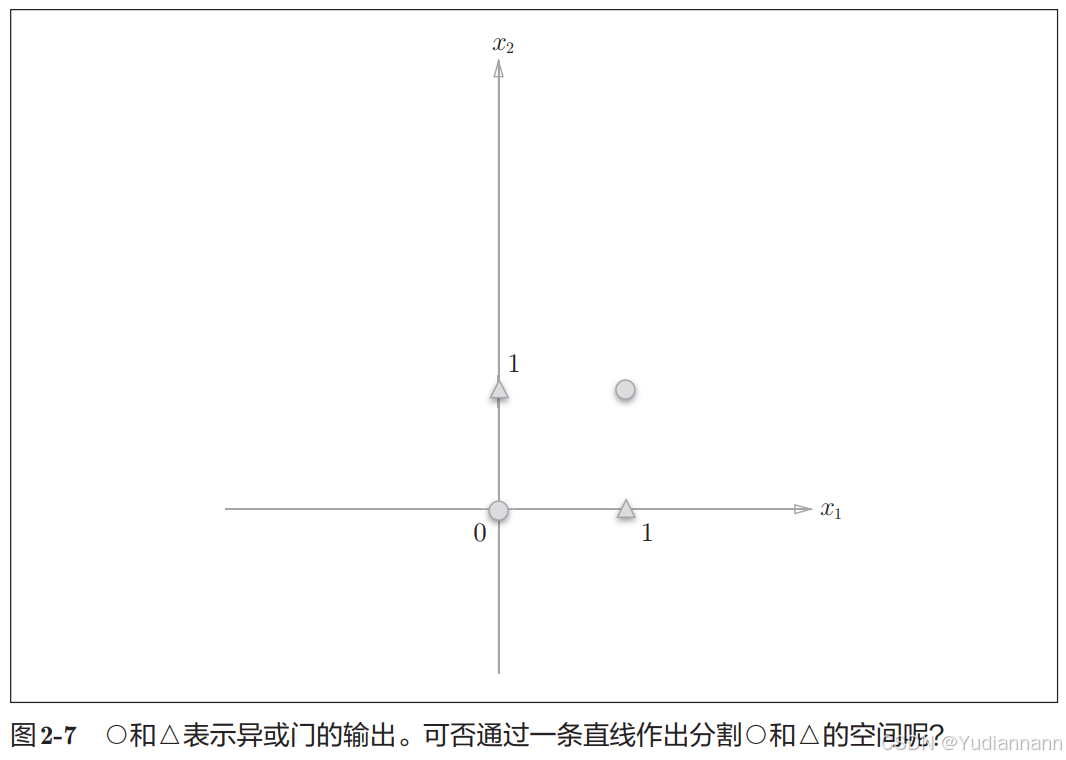
不可以用一条直线进行分类
但是可以用非直线(曲线)来分类
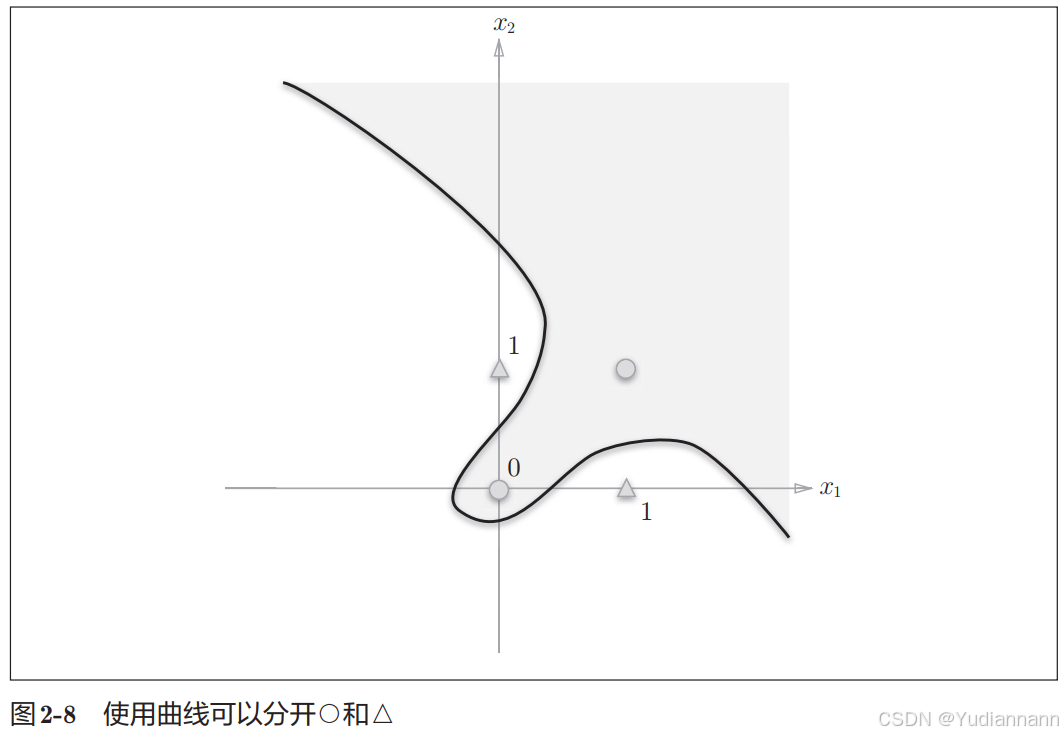
由图 2-8 这样的曲线分割而成的空间称为非线性空间,由直线分割而成的空间称为线性空间
但是使用感知机无法表示曲线
3.3 多层感知机
多层感知机(Multilayer Perceptron,MLP)
使用已有的门电路可以获得异或门:
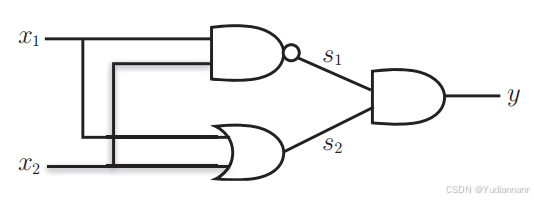
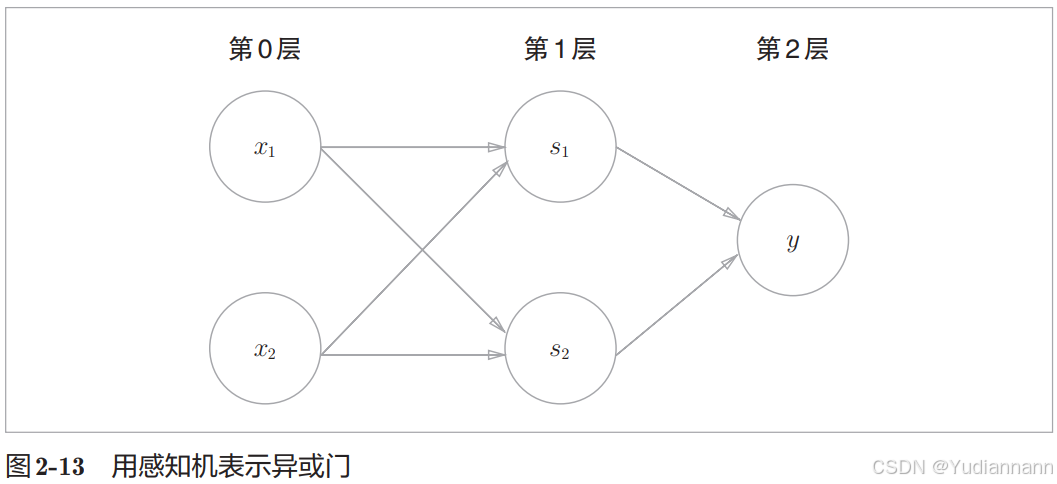

叠加了多层的感知机也称为多层感知机,理论上2层感知机可以表示任意函数(激活函数要使用 sigmoid 函数),而且可以表示计算机
4 神经网络
感知机的参数确定需要人工设置,很麻烦\
“朴素感知机”是指单层网络,指的是激活函数使用了阶跃函数的模型。“多层感知机”是指神经网络,即使用sigmoid函数(后述)等平滑的激活函数的多层网络
神经网络解决了这个问题,可以自动地从数据中学习到合适的权重参数
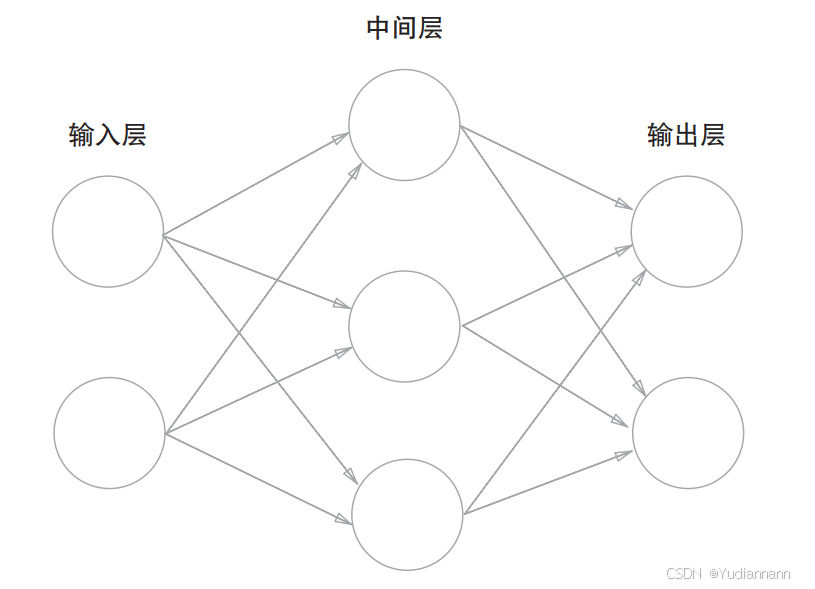
神经网络的结构:
从左到右可以称第0层、第1层、第2层
其中,中间层又称隐藏层
“隐藏”一词的意思是,隐藏层的神经元(和输入层、输出层不同)肉眼看不见
4.1 阶跃函数
虽然神经网络的激活函数不是阶跃函数,但是还是用 matplotlib 画一下
def step_function(x): if x > 0: return 1 else: return 0 简单写一下,但是这样传参不能是 numpy 数组,所以改写:
注意这里用到了 numpy 的技巧
import numpy as np import matplotlib.pyplot as plt def step_function(x): y = x > 0 return y.astype(np.int32) x = np.arange(-100, 100, 0.1) y = step_function(x) plt.plot(x, y) plt.show() 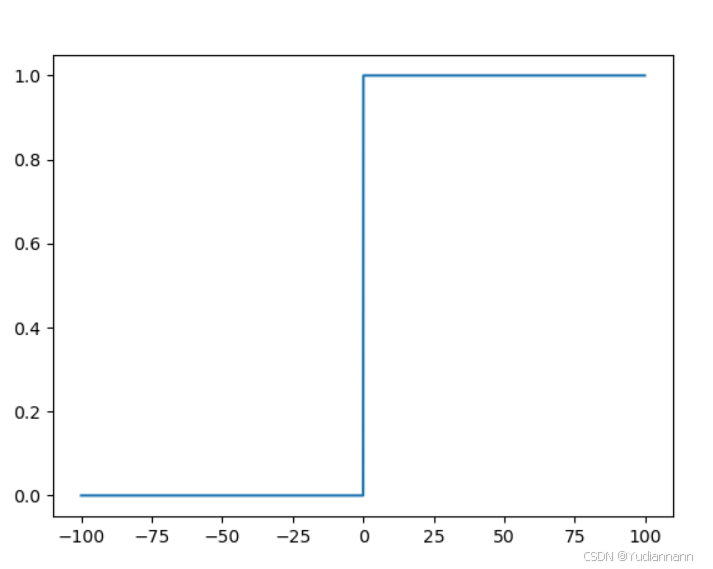
4.2 sigmoid 函数
import numpy as np import matplotlib.pyplot as plt def sigmoid(x): return 1.0 / (1.0 + np.exp(-x)) def step_function(x): y = x > 0 return y.astype(np.int32) x = np.arange(-10, 10, 1) y1 = sigmoid(x) y2 = step_function(x) plt.plot(x, y1, label="sigmoid") plt.plot(x, y2, linestyle="--", color="red", label="step_function") plt.legend() plt.show() 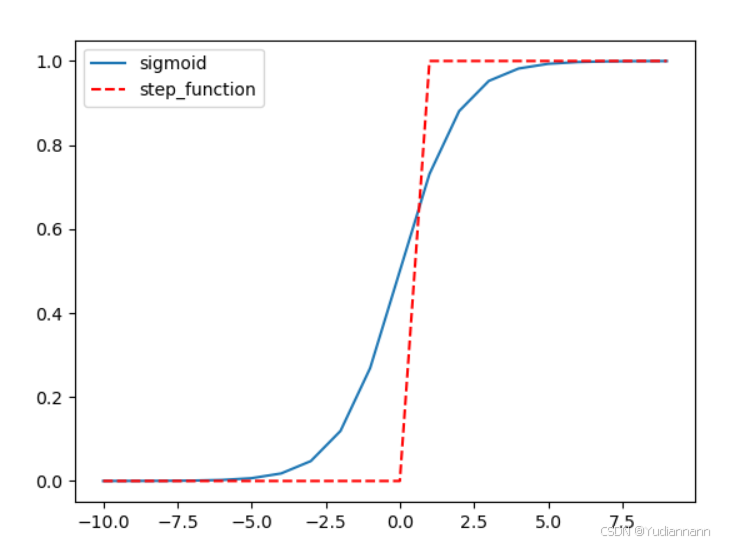
使用线性函数时,无法发挥多层网络带来的优势。因此,为了发挥叠加层所
带来的优势,激活函数必须使用非线性函数
4.3 ReLU函数
Rectified Linear Unit
ReLU 函数在输入大于 0 时,直接输出该值;在输入小于等于 0 时,输出 0
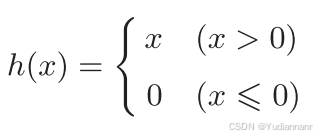
import numpy as np import matplotlib.pyplot as plt def relu(x): return np.maximum(0, x) x = np.arange(-10, 10, 0.1) y = relu(x) plt.plot(x, y) plt.show() 
4.4 三层神经网络
首先,矩阵点乘:
np.dot(x, y)
神经网络的运算可以作为矩阵运算打包进行
4.5 多维数组的运算
4.5.1 dot点乘
两种写法:
- a.dot(b)
- np.dot(a,b)
a = np.array([[2, 3], [5, 6]]) b = np.array([[1, 2], [9, 8]]) print(a.dot(b))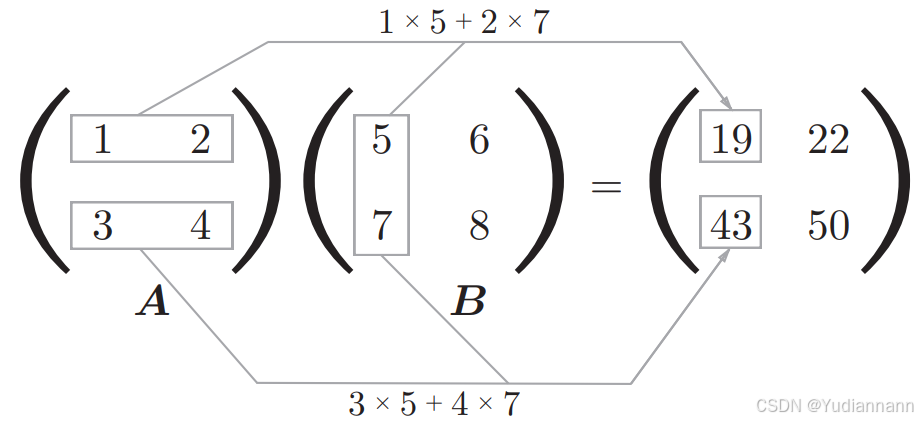
注意和普通的广播乘法区分:
# a*b
[[ 2 6]
[45 48]]# a.dot(b)
[[29 28]
[59 58]]
4.5.2 实现神经网络
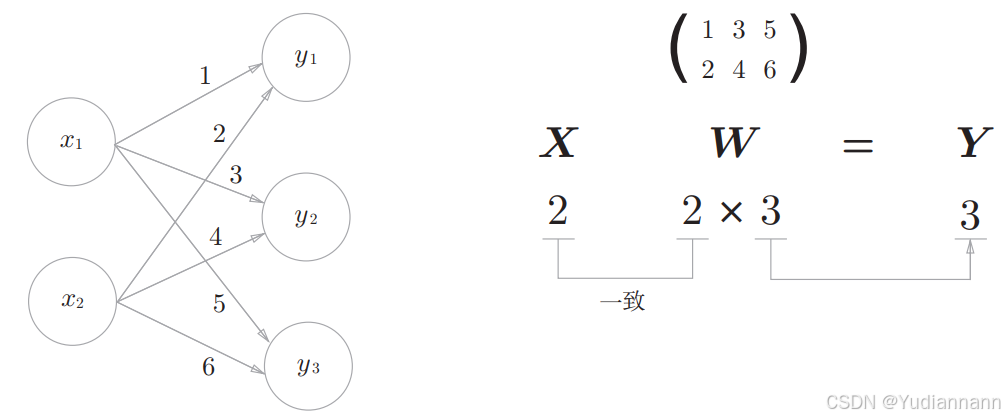
X = np.array([1, 2]) W = np.array([[1, 3, 5], [2, 4, 6]]) Y = X.dot(W) print(Y)[ 5 11 17]
4.5.3 三层神经网络的实现
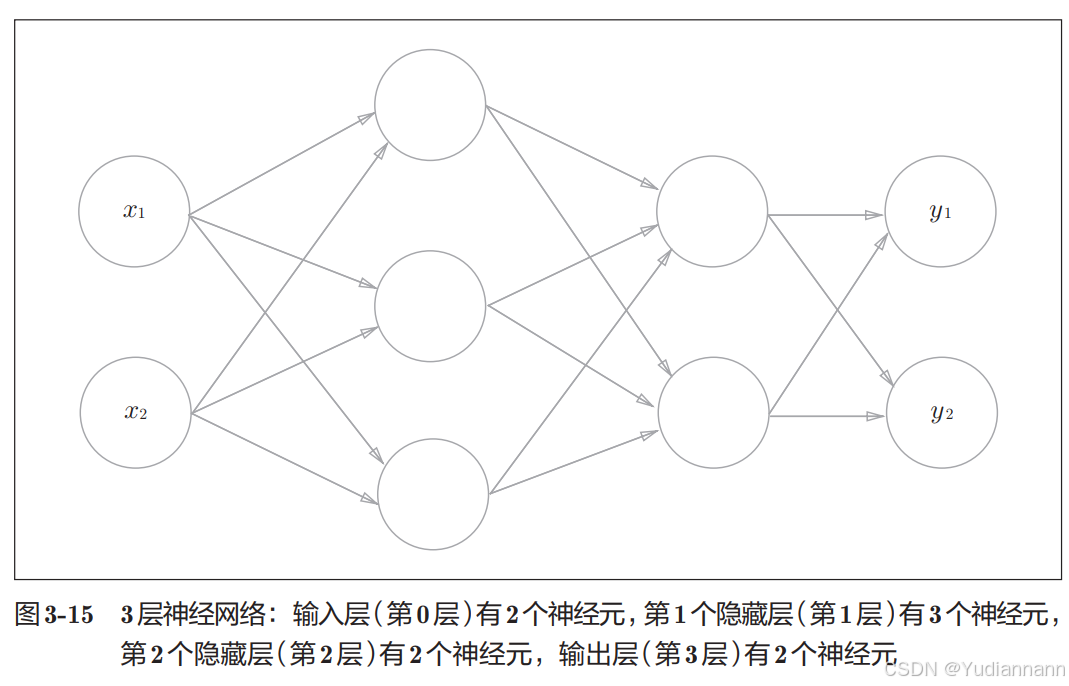
(参数是随机取的)
输入层到第1个隐藏层:
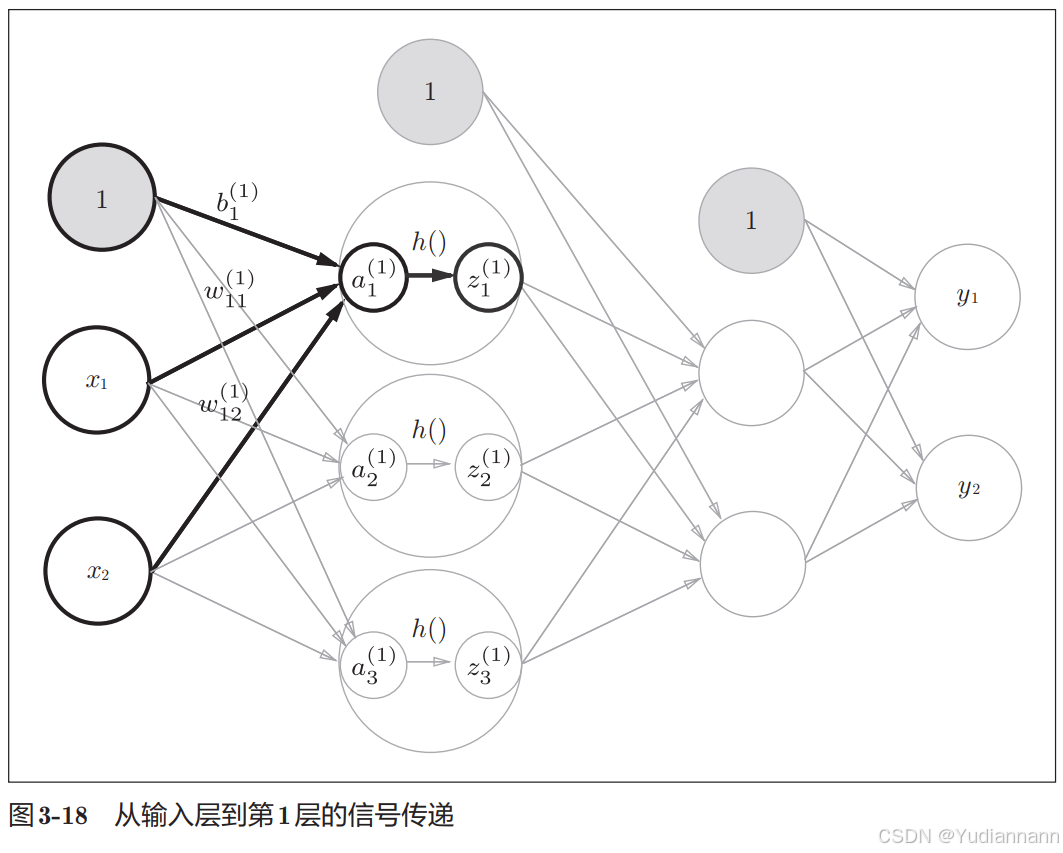
X = np.array([1.0, 0.5]) W1 = np.array([[0.1, 0.3, 0.5], [0.2, 0.4, 0.6]]) B1 = np.array([0.1, 0.2, 0.3]) A1 = X.dot(W1) + B1 Z1 = sigmoid(A1) print(Z1)[0.57444252 0.66818777 0.75026011]
第1个隐藏层到第2个隐藏层:
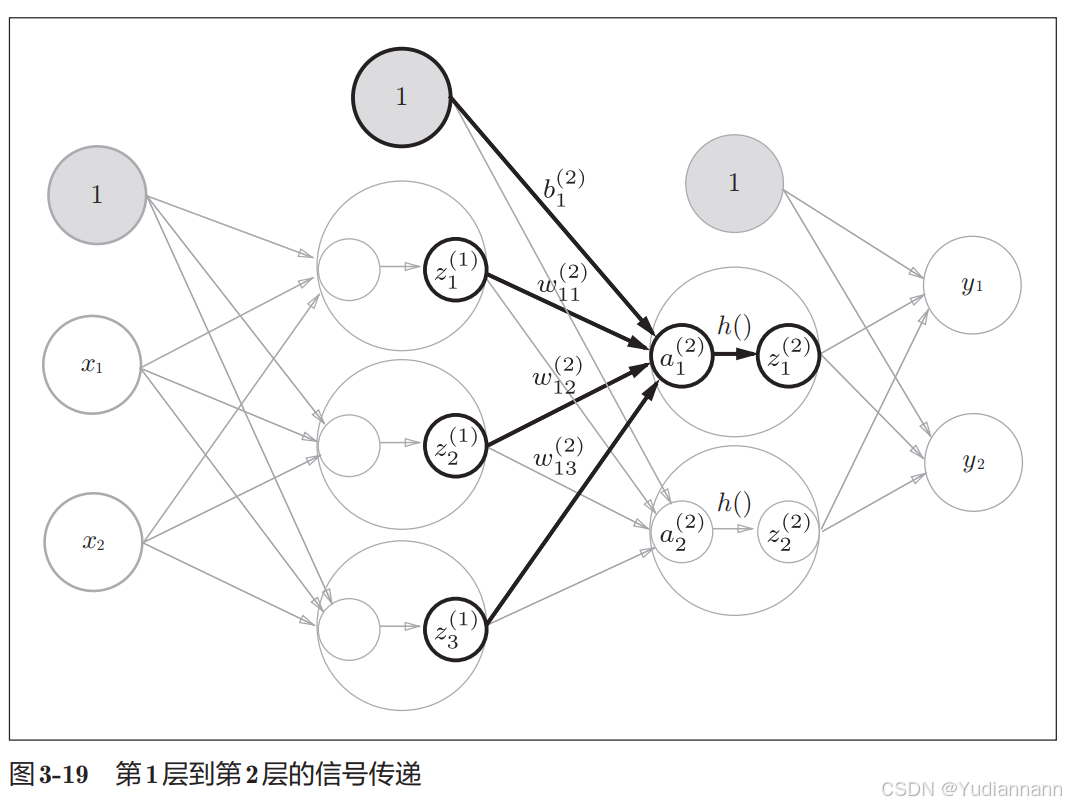
W2 = np.array([[0.1, 0.4], [0.2, 0.5], [0.3, 0.6]]) B2 = np.array([0.1, 0.2]) # 第二次传递 A2 = Z1.dot(W2) + B2 Z2 = sigmoid(A2)[0.62624937 0.7710107]
第2个隐藏层到输出层:
输出层所用的激活函数,要根据求解问题的性质决定
- 回归问题可以使用恒等函数
- 二元分类问题可以使用 sigmoid 函数
- 多元分类问题可以使用 softmax 函数
这里使用恒等函数 identity_function()
W3 = np.array([[0.1, 0.3], [0.2, 0.4]]) B3 = np.array([0.1, 0.2]) # 第三次传递 A3 = Z2.dot(W3) + B3 Y = identity_function(A3) print(Y)[0.31682708 0.69627909]
4.5.4 代码总结
import numpy as np import matplotlib.pyplot as plt def sigmoid(x): y = 1.0 / (1.0 + np.exp(-x)) return y def identity_function(x): return x def init_network(): network = {'W1': np.array([[0.1, 0.3, 0.5], [0.2, 0.4, 0.6]]), 'b1': np.array([0.1, 0.2, 0.3]), 'W2': np.array([[0.1, 0.4], [0.2, 0.5], [0.3, 0.6]]), 'b2': np.array([0.1, 0.2]), 'W3': np.array([[0.1, 0.3], [0.2, 0.4]]), 'b3': np.array([0.1, 0.2])} return network # 前向处理 def forward(network, x): W1, W2, W3 = network['W1'], network['W2'], network['W3'] b1, b2, b3 = network['b1'], network['b2'], network['b3'] a1 = np.dot(x, W1) + b1 z1 = sigmoid(a1) a2 = np.dot(z1, W2) + b2 z2 = sigmoid(a2) a3 = np.dot(z2, W3) + b3 y = identity_function(a3) return y network = init_network() x = np.array([1.0, 0.5]) y = forward(network, x) print(y) # [ 0.31682708 0.69627909] 4.6 输出层设计
神经网络可以用在分类问题和回归问题上,不过需要根据情况改变输出层的激活函数。一般而言,回归问题用恒等函数,分类问题用 softmax 函数
4.6.1 softmax 函数
softmax 函数的作用是将一个向量或一组实数转换成概率分布,使得每个元素的值都在 0 到 1 之间,并且所有元素的和为 1
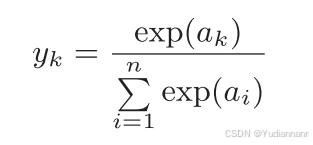
假设输出层共有 n 个神经元,计算第 k 个神经元的输出 yk,softmax 函数的分子是输入信号ak的指数函数,分母是所有输入信号的指数函数的和
但是可以省略:
4.7 -----手写数字识别-----
介绍完神经网络的结构之后,现在我们来试着解决实际问题。这里我们来进行手写数字图像的分类。假设学习已经全部结束,我们使用学习到的参数,先实现神经网络的“推理处理”。这个推理处理也称为神经网络的前向传播(forward propagation)
求解机器学习问题的步骤:
首先使用训练数据(学习数据)进行权重参数的学习;进行推理时,使用刚才学习到的参数,对输入数据进行分类
4.7.1 MNIST 数据集
MNIST 数据集是由 0 到 9 的数字图像构成的。训练图像有 6 万张,测试图像有 1 万张,MNIST的图像数据是 28 像素 × 28 像素的灰度图像(1 通道),各个像素的取值在 0 到 255 之间。每个图像数据都相应地标有标签
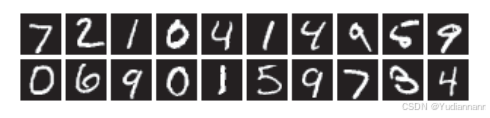
4.7.2 神经网络的推理处理
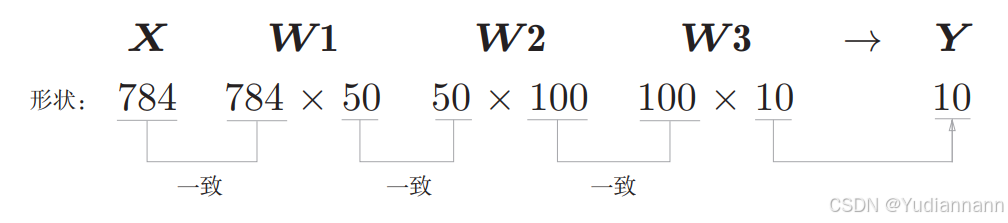
输入层共有 28 * 28 = 784 个神经元
输出层共有 10 个神经元(0~9 一共十个输出)
有 2 个隐藏层,第 1 个隐藏层有 50 个神经元,第 2 个隐藏层有 100 个神经元(人为设置)
4.7.3 批处理
批(batch)
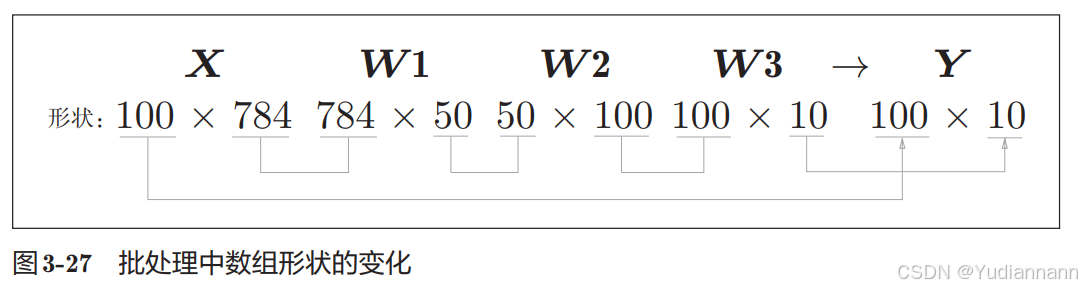
批处理一次性计算大型数组要比分开逐步计算各个小型数组速度更快
5 神经网络的学习
学习:从训练数据中自动获取最优权重参数
为了使神经网络能进行学习,将导入损失函数这一指标。而学习的目的就是以该损失函数为基准,找出能使它的值达到最小的权重参数
学习方案:
- 提取特征,再用机器学习技术学习这些特征量的模式
在计算机视觉领域,常用的特征量包括 SIFT、 SURF 和 HOG 等。使用这些特征量将图像数据转换为向量,然后对转换后的向量使用机器学习中的 SVM(支持向量机)、 KNN (K近邻算法)等分类器进行学习

- 神经网络(深度学习)
深度学习有时也称为端到端机器学习(end-to-end machine learning)这里所说的端到端是指从一端到另一端的意思,也就是从原始数据(输入)中获得目标结果(输出)的意思。
神经网络的优点是对所有的问题都可以用同样的流程来解决。比如,不管要求解的问题是识别5,还是识别狗,抑或是识别人脸,神经网络都是通过不断地学习所提供的数据,尝试发现待求解的问题的模式。也就是说,与待处理的问题无关,神经网络可以将数据直接作为原始数据,进行“端对端”的学习
5.1 损失函数
神经网络以某个指标为线索寻找最优权重参数。神经网络的学习中所用的指标称为损失函数(loss function)。这个损失函数可以使用任意函数,但一般用 均方误差 和 交叉熵误差 等
5.1.1 均方误差
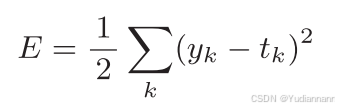
其中,yk 是表示神经网络的输出, tk 表示监督数据(训练数据), k 表示数据的维数
t = [0, 0, 1, 0, 0, 0, 0, 0, 0, 0]
t 是监督数据,将正确解标签设为 1,其他均设为 0,其他标签表示为0的表示方法称
为 one-hot 表示
5.1.2 交叉熵误差
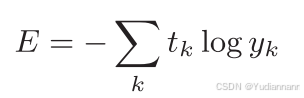
其中,yk 是表示神经网络的输出, tk 表示监督数据(训练数据), k 表示数据的维数,log表示以e为底数的自然对数(log_e)
5.2 mini_batch
我们从全部数据中选出一部分,作为全部数据的“近似”。神经网络的学习也是从训练数据中选出一批数据(称为mini-batch,小批量),然后对每个mini-batch进行学习。比如,从60000个训练数据中随机选择100笔,再用这100笔数据进行学习。这种学习方式称为 mini-batch 学习。
5.3 梯度
由全部变量的偏导数汇总而成的向量称为梯度(gradient)
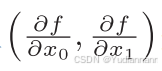
梯度指示的方向是各点处的函数值减小最多的方向
梯度下降法:
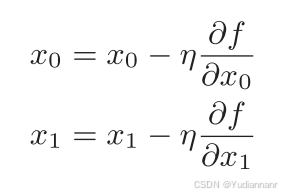
其中,η 表示更新量,在神经网络的学习中,称为学习率(learningrate)
像学习率这样的参数称为超参数。这是一种和神经网络的参数(权重和偏置)性质不同的参数。相对于神经网络的权重参数是通过训练数据和学习算法自动获得的,学习率这样的超参数则是人工设定的。一般来说,超参数需要尝试多个值,以便找到一种可以使学习顺利
进行的设定
5.3 算法实现
前提
神经网络存在合适的权重和偏置,调整权重和偏置以便拟合训练数据的过程称为“学习”。神经网络的学习分成下面4个步骤
步骤1( mini-batch)
从训练数据中随机选出一部分数据,这部分数据称为 mini-batch。我们的目标是减小mini-batch的损失函数的值
步骤2(计算梯度)
为了减小 mini-batch 的损失函数的值,需要求出各个权重参数的梯度梯度表示损失函数的值减小最多的方向
步骤3(更新参数)
将权重参数沿梯度方向进行微小更新
步骤4(重复)
重复步骤1、步骤2、步骤3
不过因为这里使用的数据是随机选择的 mini batch 数据,所以又称为随机梯度下降法(stochastic gradient descent)。“随机”指的是“随机选择的”的意思,因此,随机梯度下降法是“对随机选择的数据进行的梯度下降法”。深度学习的很多框架中,随机梯度下降法一般由一个名为 SGD 的函数来实现
epoch:
epoch 是一个单位。一个 epoch 表示学习中所有训练数据均被使用过一次时的更新次数。比如,对于 10000 笔训练数据,用大小为 100 笔数据的 mini-batch 进行学习时,重复随机梯度下降法 100 次,所有的训练数据就都被“看过”了。此时,100次就是一个 epoch
5.4 代码实现
2 层神经网络(隐藏层为 1 层的网络),使用 MNIST 数据集
(略)
6 学习技巧
