阅读量:6
分(中)位数回归算法 -医学小样本数据回归分析的更佳选择 ?
在医学研究中,小样本数据回归分析是一项常见且重要的任务。由于医学数据的复杂性、多样性和稀缺性,传统的回归分析方法如最小二乘法(OLS)在处理这类数据时可能面临诸多挑战,如异常值敏感性高、数据偏斜等。分位数回归(Quantile Regression)作为一种统计方法,以其独特的优势成为医学小样本数据回归分析的更佳选择。
分位数回归算法概述
分位数回归最早由Roger Koenker和Gilbert Bassett于1978年提出,旨在研究自变量与因变量的条件分位数之间的关系。与传统的回归分析(如OLS)不同,分位数回归不仅关注因变量的条件期望(均值),还关注其条件分位数,如中位数、25%分位数和75%分位数等。这种方法通过最小化非对称形式的绝对值残差,构建自变量与因变量分位数之间的线性关系模型。
基本原理
分位数回归的核心思想是将目标变量(因变量)设置为特定分位数,并计算该分位数的条件概率密度函数。这些密度函数描述了自变量与因变量在特定分位数下的关系。在实际操作中,通过选择不同的分位数(如0.25、0.5、0.75等),可以构建多个分位数回归模型,以全面描述因变量的条件分布。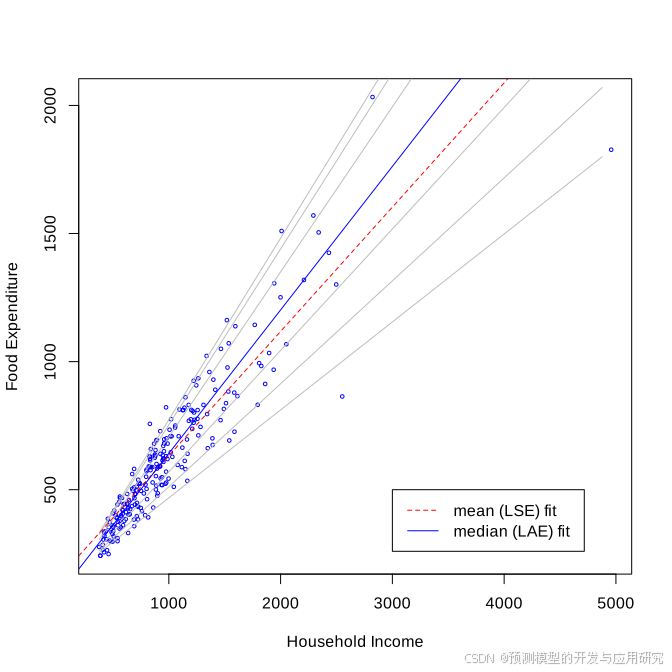
图注:红色虚线带表的是均值线性回归的拟合,蓝色线代表的是中位数回归的拟合结果,灰色线代表的其它分位数回归拟合的结果
优点
- 稳健性:分位数回归对异常值和数据偏斜不敏感,因此在处理含有异常值或偏斜分布的医学数据时具有更高的稳健性。
- 全面性:通过构建多个分位数回归模型,可以全面描述因变量的条件分布,而不仅仅是其条件期望。
- 灵活性:分位数回归不需要假设误差项的正态分布,因此适用于各种非正态分布的医学数据。
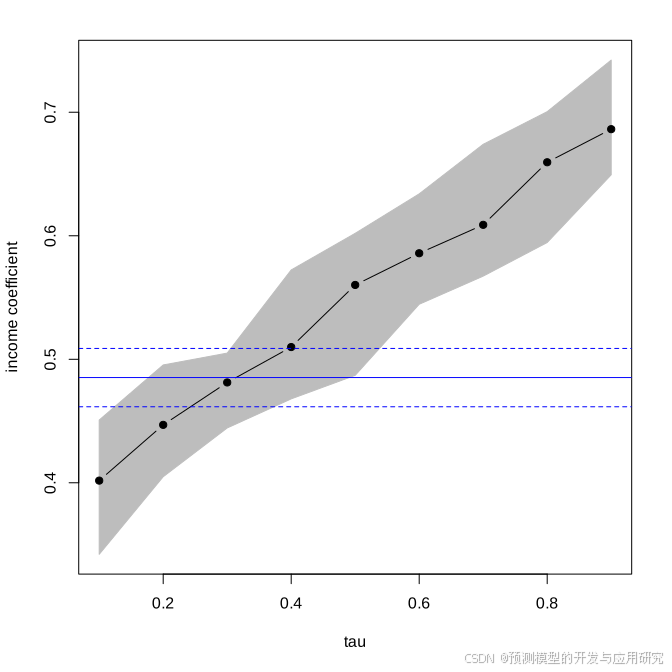
图注:横坐标是各个分位数,纵坐标是变量的回归系数,代表变量的区间不同,对预测结果的贡献也不同。
分位数回归的应用
- 变量间关系分析:在医学研究中,研究者经常需要分析多个变量之间的关系,如药物剂量与治疗效果、患者年龄与生存率等。分位数回归能够揭示这些变量在不同分位数下的关系,提供比传统回归更全面的信息。例如,在药物剂量研究中,分位数回归可以分析不同剂量下治疗效果的变化,帮助医生制定更精确的用药方案。
- 预测:分位数回归不仅可以用于变量间关系的分析,还可以用于预测。通过构建多个分位数回归模型,研究者可以预测因变量在不同分位数下的值,从而提供更精确的预测结果。
在小样本数据的优势
- 对于医学小样本数据,分位数回归的优势尤为明显。由于小样本数据往往具有较大的变异性和不确定性,传统的回归分析方法可能难以准确捕捉变量之间的关系。而分位数回归通过其稳健性和全面性,能够在小样本数据下提供更为可靠的回归分析结果。
- 下面通过实验简单比较分位数回归和均值回归:
- 检验结局变量的正态性
library(nortest) # 使用ad.test函数进行Anderson-Darling检验 ad.test(airquality$Ozone) #p值<0.001,表明数据不符合正态分布 - 分位数回归
#中位数回归预测 airq <- airquality[143:145,] f <- rq(Ozone ~ ., data=airquality)#tau=.5 predict(f,newdata=airq) #说明:中位数回归,默认是tau=0.5 #预测结果:143:48.9635248831032 144:2.72110881442428 145:17.638599052014 AIC(f) #计算结果:979.126779601049 - 均值回归
#均值回归 f_lm<-lm(Ozone ~ ., data=airquality) predict(f_lm,newdata=airq) #预测结果:143:53.0136929276497 144:5.75872297429852 145:19.3243671366314 AIC(f_lm) #计算结果:997.218772911938 - 结果:分位数回归的AIC参数高于均值回归。
结论
对于小样本回归任务,结局变量非正态分布的情况下,采用分位数回归可能是一个更好的选择。以上R代码采用quantreg包完成,更详细的代码可以参考链接。
