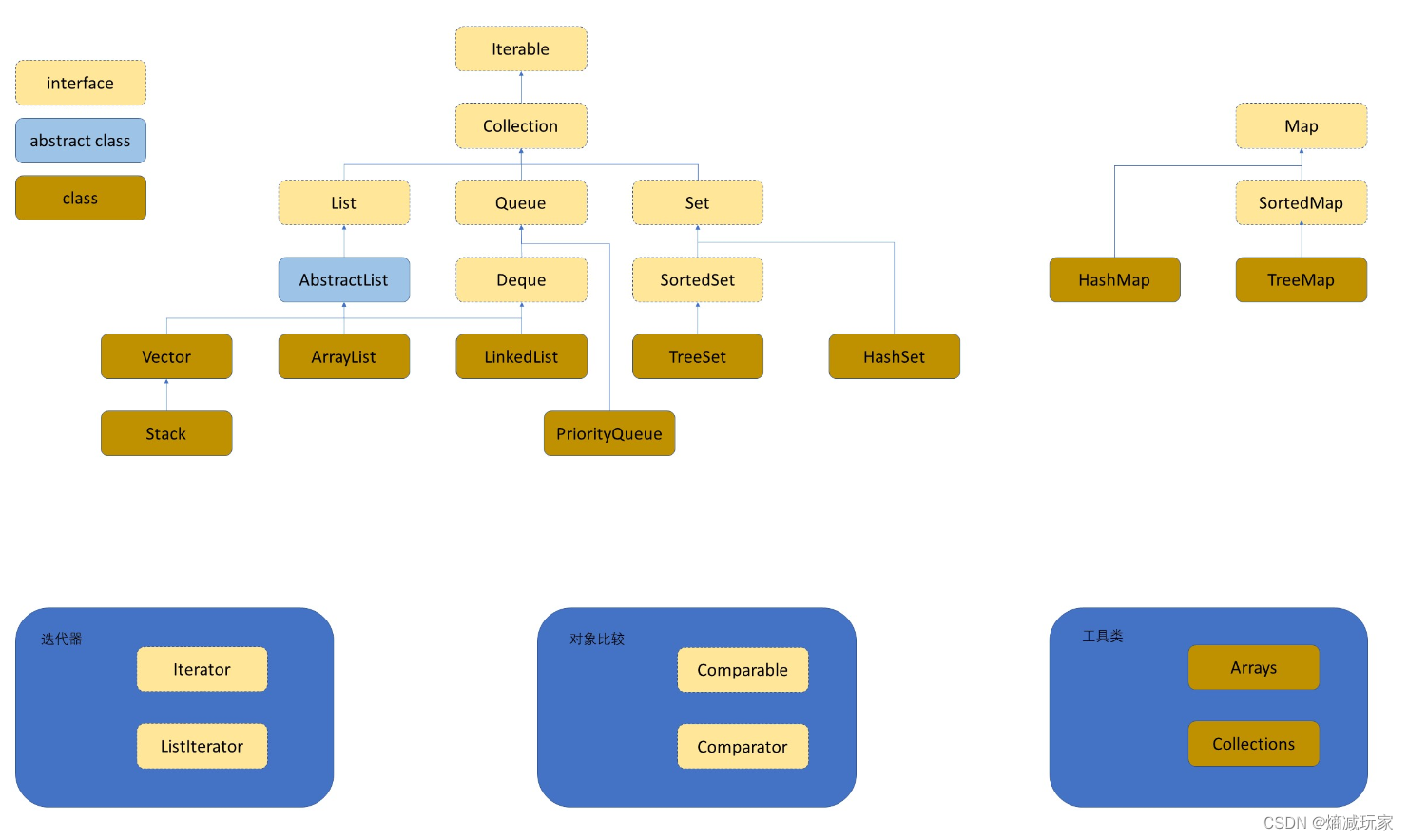
集合框架
Java 集合框架 Java Collection Framework ,又被称为容器 container ,是定义在 java.util 包下的一组接口 interfaces和其实现类 classes 。
其主要表现为将多个元素 element 置于一个单元中,对数据进行创建(Create)、读取(Retrieve)、更新(Update)和删除(Delete)的操作。即平时我们俗称的增删查改 CRUD 。
数据结构与算法的概念
数据结构(Data Structure)是计算机存储、组织数据的方式,指相互之间存在一种或多种特定关系的数据元素的
集合。
算法(Algorithm):就是定义良好的计算过程,他取一个或一组的值为输入,并产生出一个或一组值作为输出。简单来说算法就是一系列的计算步骤,用来将输入数据转化成输出结果。
时间复杂度和空间复杂度
算法效率分析分为两种:第一种是时间效率,第二种是空间效率。时间效率被称为时间复杂度,而空间效率被称作空间复杂度。 时间复杂度主要衡量的是一个算法的运行速度,而空间复杂度主要衡量一个算法所需要的额外空间,
由于计算机的飞速发展,计算机的存储容量得到大幅度提高,因此我们现在主要考虑时间复杂度。
时间复杂度
时间复杂度的定义:在计算机科学中,算法的时间复杂度是一个数学函数,它定量描述了该算法的运行时间。一个算法执行所耗费的时间,从理论上说,是不能算出来的,只有你把你的程序放在机器上跑起来,才能知道。但是我们需要每个算法都上机测试吗?是可以都上机测试,但是这很麻烦,所以才有了时间复杂度这个分析方式。一个算法所花费的时间与其中语句的执行次数成正比例,算法中的基本操作的执行次数,为算法的时间复杂度。
因此我们使用计算机执行语句的次数来表示时间复杂度,但是在实际中我们计算时间复杂度时,我们其实并不一定要计算精确的执行次数,而只需要大概执行次数,那么这里我们使用大O的渐进表示法。
大O渐进法使用规则:
1、用常数1取代运行时间中的所有加法常数。
2、在修改后的运行次数函数中,只保留最高阶项。
3、如果最高阶项存在且不是1,则去除与这个项目相乘的常数。得到的结果就是大O阶。
一个算法面对不同的问题时,执行语句的次数也会由此不一样,例如我们在一个数组里查找一个数据,如果这个数据就是第一个,那执行次数就是1次,如果是最后一个,那执行次数就是整个数组的长度,也就是算法的执行情况,有三种,最好的情况,平均情况,最坏情况。时间复杂度取算法的最坏情况,因为最坏情况下都能接受,那这个算法就是一个好的算法。
例题:
//求func2的时间复杂度 void func2(int N){ int count = 0; for (int i = 0; i < 2 * N; i++) { count++; } int m = 10; while(m-- > 0){ count++; } } 首先for循环语句一共执行2N次,while语句执行10次,一共执行2N+10 次,使用大O渐进法表示,保留最高阶,剩下2*N,去除2,剩下N,所以时间复杂度为O(N)
void func3(int N,int M){ int count = 0; for (int i = 0; i < N; i++) { count++; } for (int i = 0; i < M; i++) { count++; } } 一共执行次数为N+M,即时间复杂度为O(N+M)
void func4(){ int count = 0; for (int i = 0; i < 100; i++) { count++; } } 语句执行次数为100,是常数化为1,则时间复杂度为O(1)
void bubbleSort(int[] array){ boolean flag = true; for (int i = 0; flag && i < array.length - 1; i++) { flag = false; for (int j = i; j < array.length - i - 1; j++) { if(array[j] > array[j+1]){ int tmp = array[j]; array[j] = array[j+1]; array[j+1] = tmp; flag = true; } } } } 上面这个是冒泡排序算法,时间复杂度取最坏的情况,假设数组的长度为N,第一轮冒泡排序的执行次数为N-1,第二困轮冒泡排序的执行次数为N-2,以此类推,这个是一个等差数列,使用等差数列的求和公式为N(N-1)/2,使用大O渐进法表示O(N^2)
int binarySearch(int[] array, int value) { int begin = 0; int end = array.length - 1; while(begin < end){ int mid = (begin + end) / 2; if(array[mid] > value){ end = mid - 1; }else if(array[mid] < value){ begin = mid + 1; }else{ return mid; } } return -1; } 二分查找,每次查找,待查询数据都会减少一半,直到数据只剩下一个,假设查找的次数为x,数据总数为N,
(1/2)^ x * N = 1 ; x = logN (以2为底数的对数)
long factorial(int N) { return N < 2 ? N : factorial(N-1) * N; } 上面是一个求阶乘的递归算法,递归算法的执行次数等于 递归调用次数*每次递归执行的语句次数,所以这个算法的执行总次数 N-2(N>2时)或者 1 (N == 1 || N == 2),时间复杂度为O(N)
int fibonacci(int N) { return N < 2? N : fibonacci(N - 1)+fibonacci(N-2); } 我们画个图:假设求第八个斐波那契数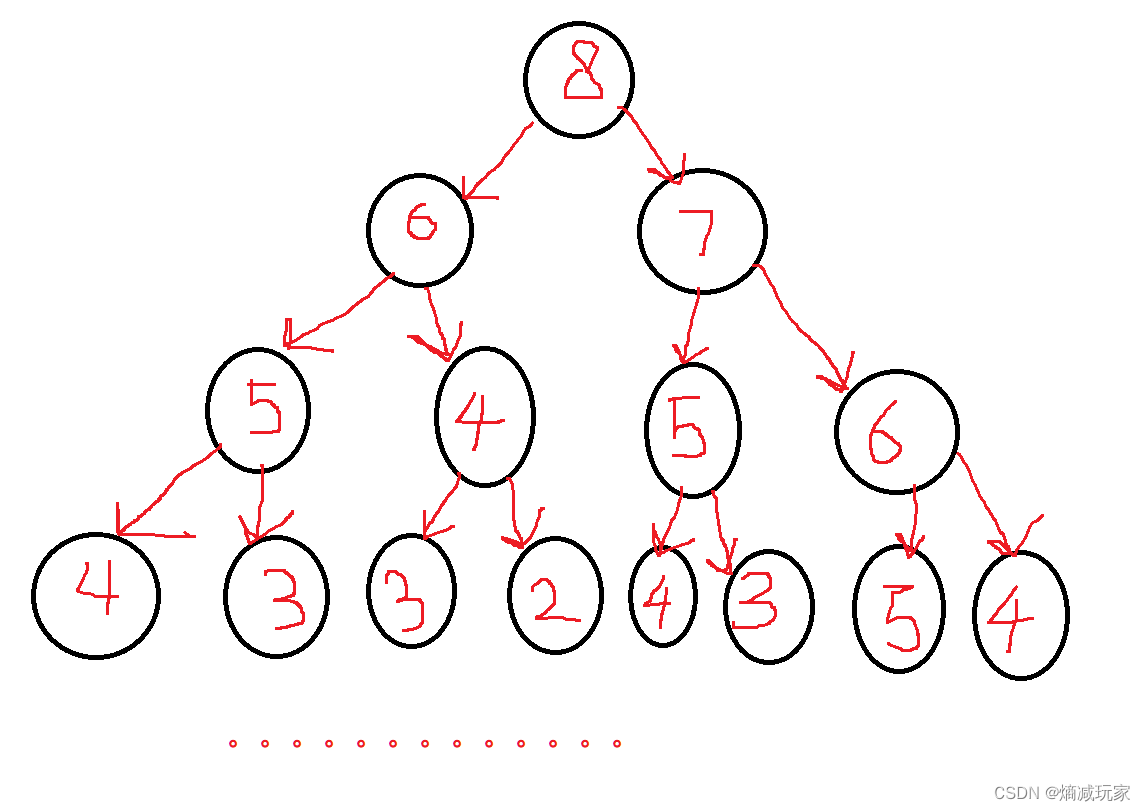
一般情况下,每求一个数都会进行两次递归才能求出,以此类推,时间复杂度为O(N^2)
空间复杂度
空间复杂度是对一个算法在运行过程中临时占用存储空间大小的量度 。空间复杂度不是程序占用了多少bytes的空间,因为这个也没太大意义,所以空间复杂度算的是变量的个数。空间复杂度计算规则基本跟时间复杂度类似,也使用大O渐进表示法。
例题:
void bubbleSort(int[] array){ boolean flag = true; for (int i = 0; flag && i < array.length - 1; i++) { flag = false; for (int j = i; j < array.length - i - 1; j++) { if(array[j] > array[j+1]){ int tmp = array[j]; array[j] = array[j+1]; array[j+1] = tmp; flag = true; } } } } 冒泡排序使用了一个数组的空间和几个变量的空间,这是常数,所以空间复杂度为O(1)
// 计算fibonacci的空间复杂度? int[] fibonacci(int n) { long[] fibArray = new long[n + 1]; fibArray[0] = 0; fibArray[1] = 1; for (int i = 2; i <= n ; i++) { fibArray[i] = fibArray[i - 1] + fibArray [i - 2]; } return fibArray; } 新建了一个数组,大小为N+1,则空间复杂度为O(N)
// 计算阶乘递归Factorial的空间复杂度? long factorial(int N) { return N < 2 ? N : factorial(N-1)*N; } 空间复杂度为O(N)
int fibonacci(int N) { return N < 2? N : fibonacci(N - 1)+fibonacci(N-2); } 要注意递归开辟的空间是可以重复利用的,所以如果一个递归要用到之前递归就开辟好的空间,是可以直接拿过来使用的,不用额外开辟新的空间,所以时间复杂度为O(N)
包装类
在Java中,由于基本类型不是继承自Object,为了在泛型代码中可以支持基本类型,Java给每个基本类型都对应了一个包装类型。
| 基本数据类型 | 包装类 |
|---|---|
| byte | Byte |
| short | Short |
| int | Integer |
| long | Long |
| float | Float |
| double | Double |
| char | Character |
| boolean | Boolean |
这里要注意两个包装类,Integer 和 Charater ,除了它们两个之外,其他的包装类都是大写开头即可。
自动装箱(显示装箱)和自动拆箱(显示拆箱)
装箱是指把基本数据类型变为包装类类型的过程。
public static void main(String[] args) { int a = 10; Integer b = Integer.valueOf(a);//显示装箱 Integer c = 10;//自动装箱 } 显示装箱是我们自己调用了 valueOf 的方法,自动装箱是底层帮我们自动调用 valueOf 方法
拆箱是指把包装类类型变为基本数据类型的过程
public static void main(String[] args) { Integer a = 10; int b = a;//自动拆箱 int c = a.intValue();//显示拆箱 double d = a.doubleValue();//显示拆箱 System.out.println(b); System.out.println(c); System.out.println(d); } 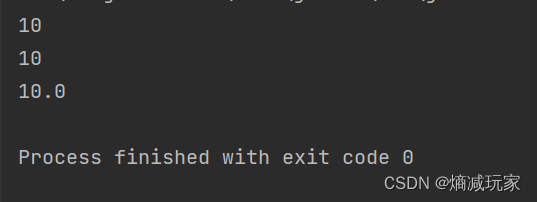
自动拆箱是底层帮我们自动调用Value,显示拆箱就是我们自己调用这个方法,我们可以使用不同的拆箱方法来将数据转化成你想要的基本数据类型,所以Integer这个包装类可以转化成不同的基本数据类型。
面试题
说出下面代码的输出结果:
public static void main(String[] args) { Integer a = 127; Integer b = 127; Integer c = 128; Integer d = 128; System.out.println(a == b); System.out.println(c == d); } 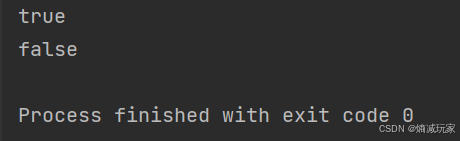
思路:要想知道结果为什么,我们就要知道装箱的源码:
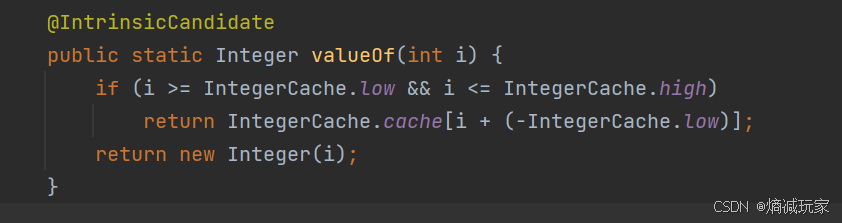
当 i 大于等于IntegerCache.low && i 小于等于 IntegerCache.high 时,就会返回数组的某一个数值,否则就会创建一个新对象,如果是返回数组的某一个数值时,那么拆箱比较之后的结果就是相等的,如果创建的是新对象,那进行 == 的比较就是对引用数据类型进行比较时,两个对象不同时那结果自然不用。
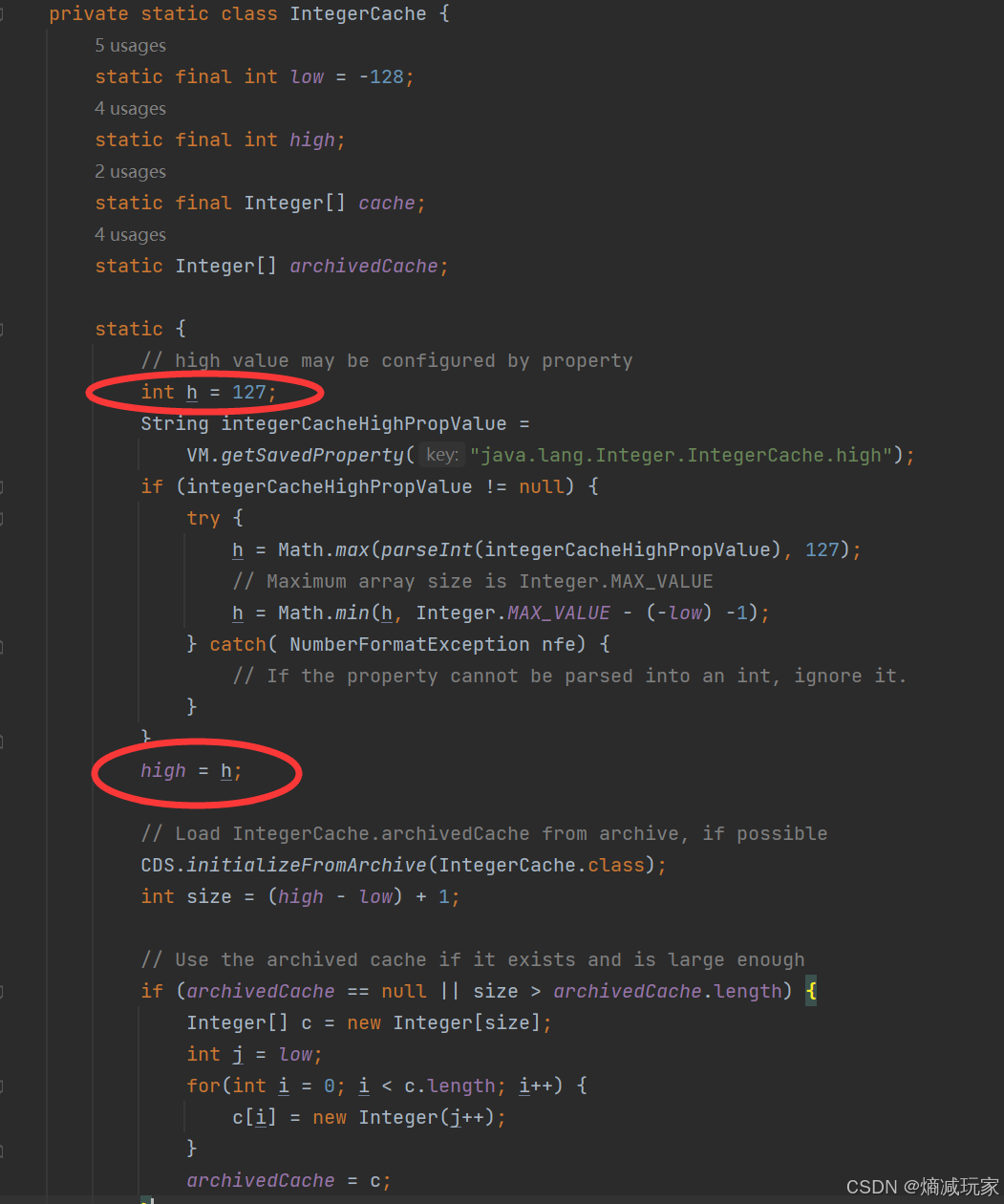
我们翻开IntederCache 数组时,我们可以发现low = -128,high = 127,所以装箱127的时候,就是直接取数组的值,如果装箱128的时候,就会创建新对象,所以结果就是true false
泛型
一般的类和方法,只能使用具体的类型: 要么是基本类型,要么是自定义的类。如果要编写可以应用于多种类型的代码,这种刻板的限制对代码的束缚就会很大。
泛型是在JDK1.5引入的新的语法,通俗讲,泛型:就是适用于许多类型。从代码上讲,就是对类型实现了参数化。
实现一个类,类中包含一个数组成员,使得数组中可以存放任何类型的数据,也可以根据成员方法返回数组中某个下标的值?
class MyArray { public Object[] array = new Object[10]; public void setArray(int pos, Object value) { array[pos] = value; } public Object getArray(int pos) { return array[pos]; } } public class Test2 { public static void main(String[] args) { MyArray arr = new MyArray(); arr.setArray(0,10); arr.setArray(1,"String"); arr.setArray(2,3.14); int a = (int)arr.getArray(0); String str = (String)arr.getArray(1); double b = (double)arr.getArray(2); System.out.println(a); System.out.println(str); System.out.println(b); } } 我们会创建一个Object[]的数组,因为Object是所有类的父类,所以这种数组可以接受不同的数据类型,当我们拿取数组的数组的时候,由于是Object类,就需要强制类型转化。
虽然在这种情况下,当前数组任何数据都可以存放,但是,更多情况下,我们还是希望他只能够持有一种数据类型。而不是同时持有这么多类型。
语法
泛型的主要目的:就是指定当前的容器,要持有什么类型的对象。让编译器去做检查。此时,就需要把类型作为参数传递。需要什么类型,就传入什么类型
创建
class 泛型类名称<类型形参列表> { // 这里可以使用类型参数 } 类型形参一般使用一个大写字母表示,常用的名称有:
E 表示 Element
K 表示 Key
V 表示 Value
N 表示 Number
T 表示 Type
S, U, V 等等,第二、第三、第四个类型
使用
泛型类<类型实参> 变量名; // 定义一个泛型类引用 new 泛型类<类型实参>(构造方法实参); // 实例化一个泛型类对象 实例:
MyArray<Integer> list = new MyArray<Integer>(); 要注意:类型形参我们在使用的时候,我们需要使用的是引用数据类型,不能使用基本数据类,所以我们要使用整型的时候,我们应该使用包装类Integer,但是不能使用int。
类型推导(Type Inference)
当编译器可以根据上下文推导出类型实参时,可以省略类型实参的填写
MyArray<Integer> list = new MyArray<>(); // 可以推导出实例化需要的类型实参为 Integer 我们把上面的包含Object数组的类改写成泛型类:
class MyArray<E>{ public Object[] array = new Object[10]; public void setArray(int pos, E value){ array[pos] = value; } public E getAaary(int pos){ return (E)array[pos]; } } 由于是泛型,这里使用E,但是我们还是使用Object数组接收不同类型的数据,数据的类型是Object,返回值是E,所以在返回数据的时候我们需要强制类型转化
裸类型(Raw Type)
裸类型是一个泛型类但没有带着类型实参
MyArray arr = new MyArray(); 注意: 我们不要自己去使用裸类型,裸类型是为了兼容老版本的 API 保留的机制
我们将上面的代码来实践一下使用:
public static void main(String[] args) { MyArray<String> arr1 = new MyArray<String>(); MyArray<Integer> arr2 = new MyArray<>();//类型推导,省略后面的类型 MyArray arr3 = new MyArray();//裸类型不推荐使用,没有编译器检查,是为了兼容老版本 } 小结:
1.泛型是将数据类型参数化,进行传递
2.例如:使用 < T > 表示当前类是一个泛型类。
3.泛型目前为止的优点:数据类型参数化,编译时自动进行类型检查和转换
擦除机制
泛型的引入是JDK5开始引入的,在JDK5之前是没有泛型的,所以裸类型是为了兼容JDK5之前的版本,从JDK5版本后泛型使用的是擦除机制。
在编译的过程当中,将所有的T替换为Object这种机制,我们称为:擦除机制。
由于Java会进行静态类型检查,所以如果你使用Integer的泛型,就不能使用String,double等数据进行赋值。
泛型的上界
在定义泛型类时,有时需要对传入的类型变量做一定的约束,可以通过类型边界来约束。
class 泛型类名称<类型形参 extends 类型边界> { //... } 举个例子:
public class MyArray<E extends Number> { //... } 这时候我们传入的类型形参就必须是Number或者是Number的子类
public static void main(String[] args) { Array<Integer> arr1 = new Array<>(); Array<Double> arr2 = new Array<>(); Array<String> arr3 = new Array<String>();//编译错误 err } Integer和Double 都是Number 的子类,String 不是Number 的子类,所以使用String 会发生编译报错。
public class MyArray<E extends Comparable<E>> { ... } 这时候E就必须实现Comparable接口
泛型方法
方法限定符 <类型形参列表> 返回值类型 方法名称(形参列表) { ... } 举个例子:
public<E extends Comparable<E>> E find(E[] arr){ //... } public static <E extends Comparable<E>> void find(){ //... } 方法的泛型类型形参写在 public 等访问权限修饰符 和 static 后面,并且类型形参要保持一致,就是如果使用E就必须统一使用E,不能混用别的类型形参(T等等)
使用:
调用泛型方法时,我们可以在方法前面加上类型参数或者不使用类型参数,和上面一样也有类型推导的机制。
public static void main(String[] args) { Integer[] a = {1,2,3,4,5,6}; MyArray.find(a); MyArray.<Integer>find(a); } 