本期,将给大家带来的是关于 LeetCode 的关于二叉树的题目讲解。
目录
(一)606. 根据二叉树创建字符串
首先,第一道题是关于 二叉树创建字符串的题,接下来我将一步步的分析带大家理解这道题!
题目如下 :👇
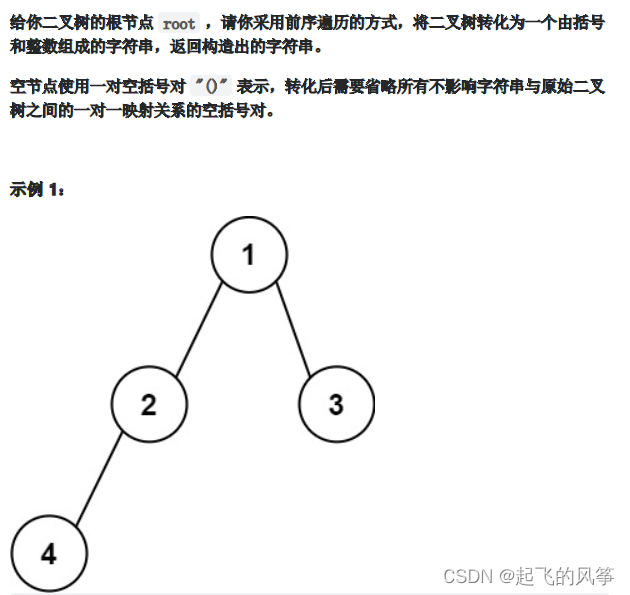
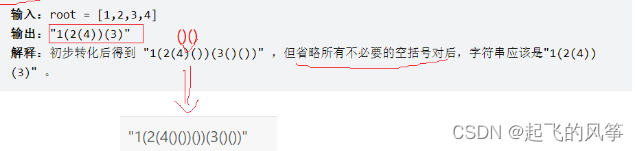
输入:root = [1,2,3,4] 输出:"1(2(4))(3)" 解释:初步转化后得到 "1(2(4)())(3()())" ,但省略所有不必要的空括号对后,字符串应该是"1(2(4))(3)" 。 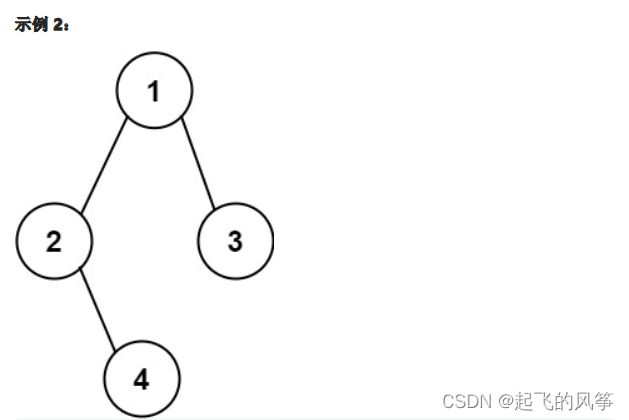
输入:root = [1,2,3,null,4] 输出:"1(2()(4))(3)" 解释:和第一个示例类似,但是无法省略第一个空括号对,否则会破坏输入与输出一一映射的关系。 💥题意分析
首先,我们还是先对题意进行简单的分析:
我们可以发现他不是把所有的输出都给用括号括起来,仔细观察发现而是有些直接省略了,具体省略的有以下几种情况:
- 1、左右都为空——省略
- 2、左为空,右不为空——不省略
- 3、右为空,左不为空——省略
但是大家仔细观察可以发现,此时当我们按照上述方式去看示例时,发现跟题意对不上。个人觉得应该是题当时弄错了,本题的整体思路就如上述,具体应该如下才对:
- 总之大概意思就是根据题意给出的二叉树的,我们按照合适的输出方案输出即可
💥解题思路
具体思路如下:
我们可以使用递归的方法得到二叉树的前序遍历,并且每次递归时加上相应的括号即可得到最终的结果。
1、如果当前节点没有孩子(即左右都为空),此时则不需要在节点后面加上任何括号;
2、如果当前节点只有左孩子,而右为空。那我们在递归时,只需要在左孩子的结果外加上一层括号,而不需要给右孩子加上任何括号;
3、对应的,如果当前节点只有右孩子,而左为空。那当我们在递归时,此时的括号就不难省略了。此时需要先加上一层空的括号表示左孩子为空,再对右孩子进行递归,并在结果外加上一层括号。
💥代码展示:
class Solution { public: string tree2str(TreeNode* root) { if(root == nullptr) return ""; //root->val不支持转成整形,因此这里加上to_string 即可实现转成字符串 string str=to_string(root->val); //左为空,此时我们不能直接省略,还要看右边的情况 if(root->left || root->right) { str+="("; str+=tree2str(root->left); str+=")"; } if(root->right) { str+="("; str+=tree2str(root->right); str+=")"; } return str; } };- 最终结果:
(二)102. 二叉树的层序遍历
题目如下 :👇
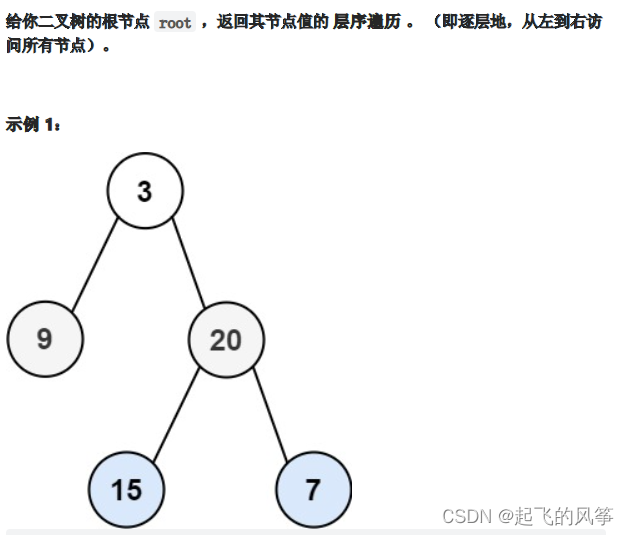
输入:root = [3,9,20,null,null,15,7] 输出:[[3],[9,20],[15,7]]示例 2:
输入:root = [1] 输出:[[1]]示例 3:
输入:root = [] 输出:[]💥题意分析
- 本题的意思其实很简答,就是根据给出的二叉树,我们相当于层序遍历之后输出最后的结果即可!
💥解题思路
在这里我给出两种思路供大家参考:
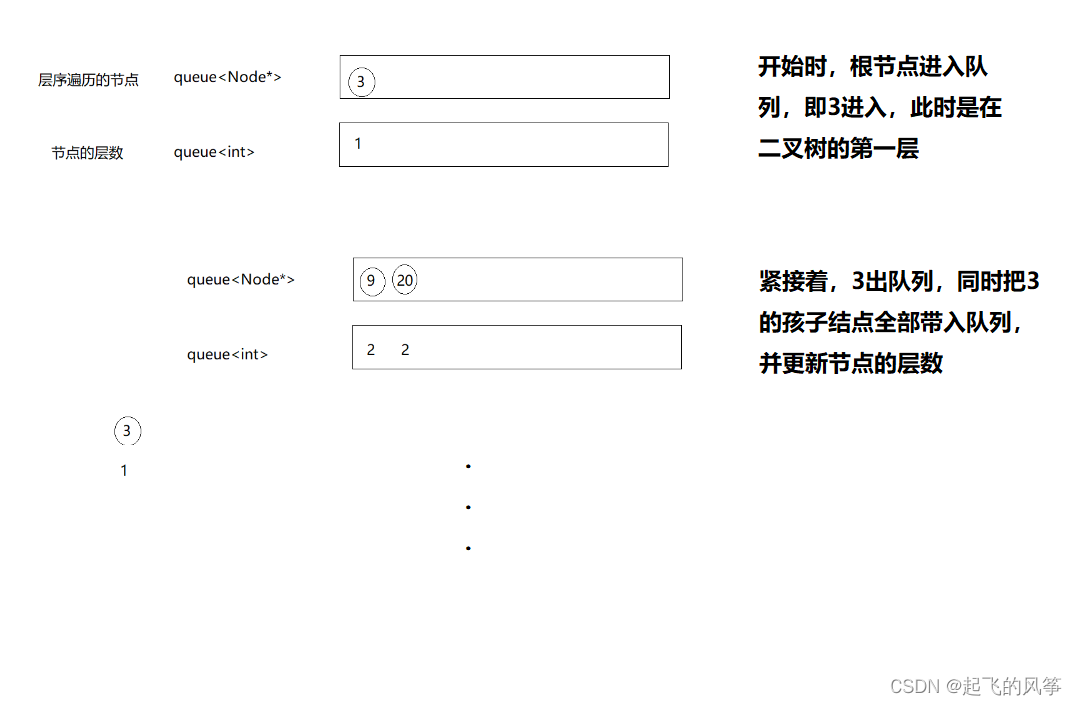
1、我们定义两个队列。
- 一个队列控制结点的指针,然后去控制层序遍历;
- 另外一个队列则为一个整形,控制层数,即此时是第几层的在进行操作。
图解:
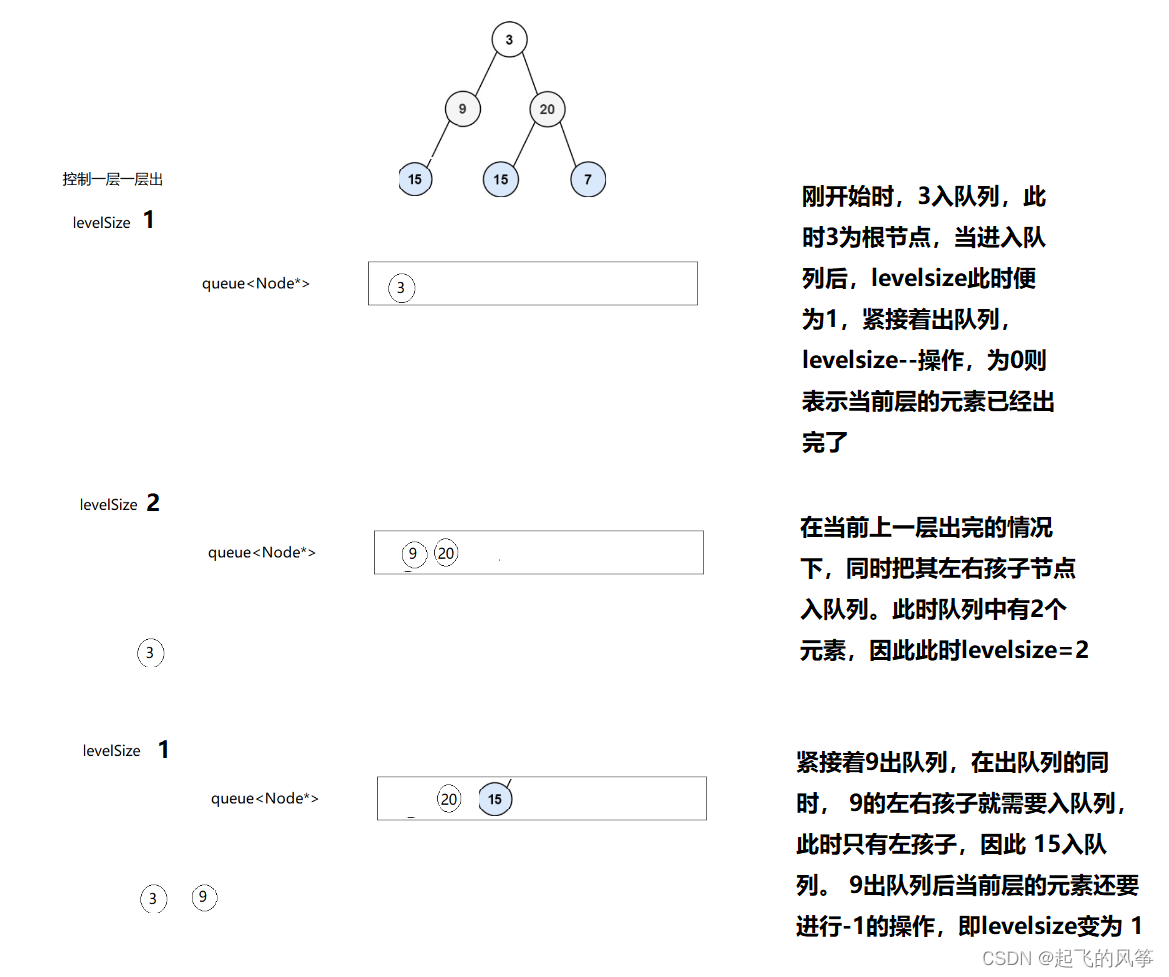
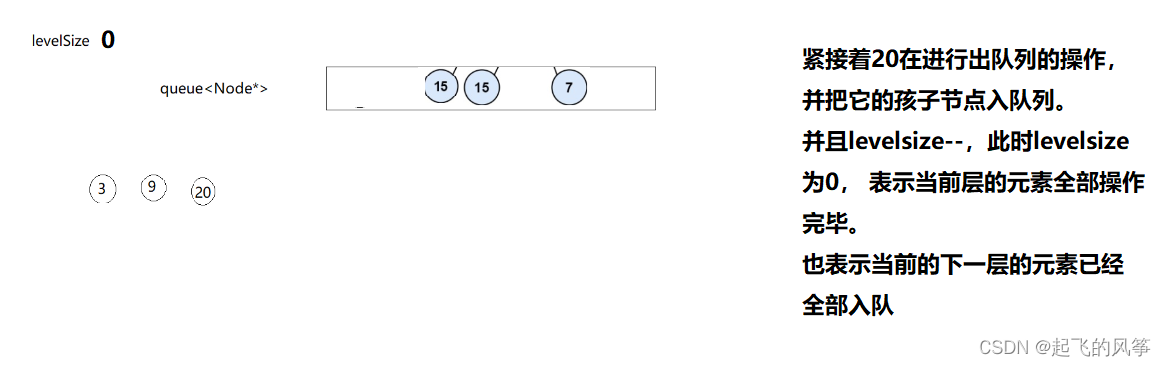
2、我们只定义一个队列。
我们也可以定义一个队列进行操作:
此时我们还需要在定义一个变量,设为【levelsize】。目的是为了控制二叉树一层一层的出;
图解:
💥代码展示:
class Solution { public: vector<vector<int>> levelOrder(TreeNode* root) { queue<TreeNode*> str; int levelsize=0; if(root) { str.push(root); levelsize=1; } //控制每层的元素出队列 vector<vector<int>>arry; while(!str.empty()) { vector<int>v; //levelsize 为几就表示需要出几次 while(levelsize--) { //先取对头的数据 TreeNode* front=str.front(); str.pop(); v.push_back(front->val); //左不为空,把元素入队 if(front->left) str.push(front->left); //右不为空,把元素入队 if(front->right) str.push(front->right); } //每层出的元素放到相应的数组中 arry.push_back(v); levelsize=str.size(); } return arry; } };- 最终结果:
(三)236. 二叉树的最近公共祖先
题目如下 :👇
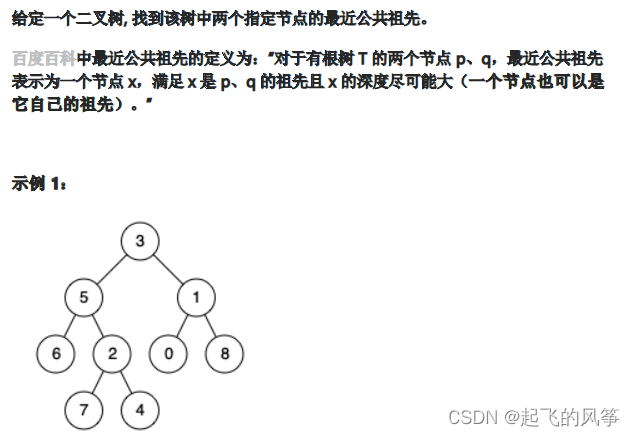
输入:root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1 输出:3 解释:节点 5 和节点 1 的最近公共祖先是节点 3 。 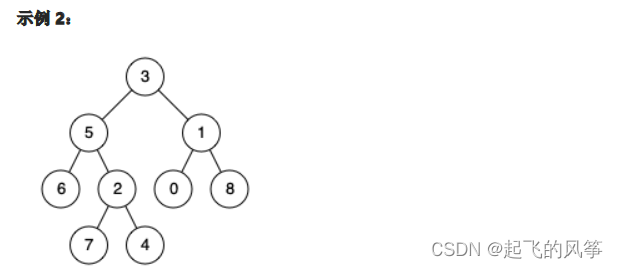
输入:root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4 输出:5 解释:节点 5 和节点 4 的最近公共祖先是节点 5 。因为根据定义最近公共祖先节点可以为节点本身。 
💥题意分析
- 本题的大概意思就是题中给出两个节点,在二叉树中我们去找到这两个节点的公共父结点输出即可!
💥解题思路
思路一:
整体思路就是DFS求出p和q 的路径放到容器中,转换成路径相交。
我们用栈来充当这个容器,定义Ppath为当前节点左端的路径,qpath为右端的节点路径;
- 图解:
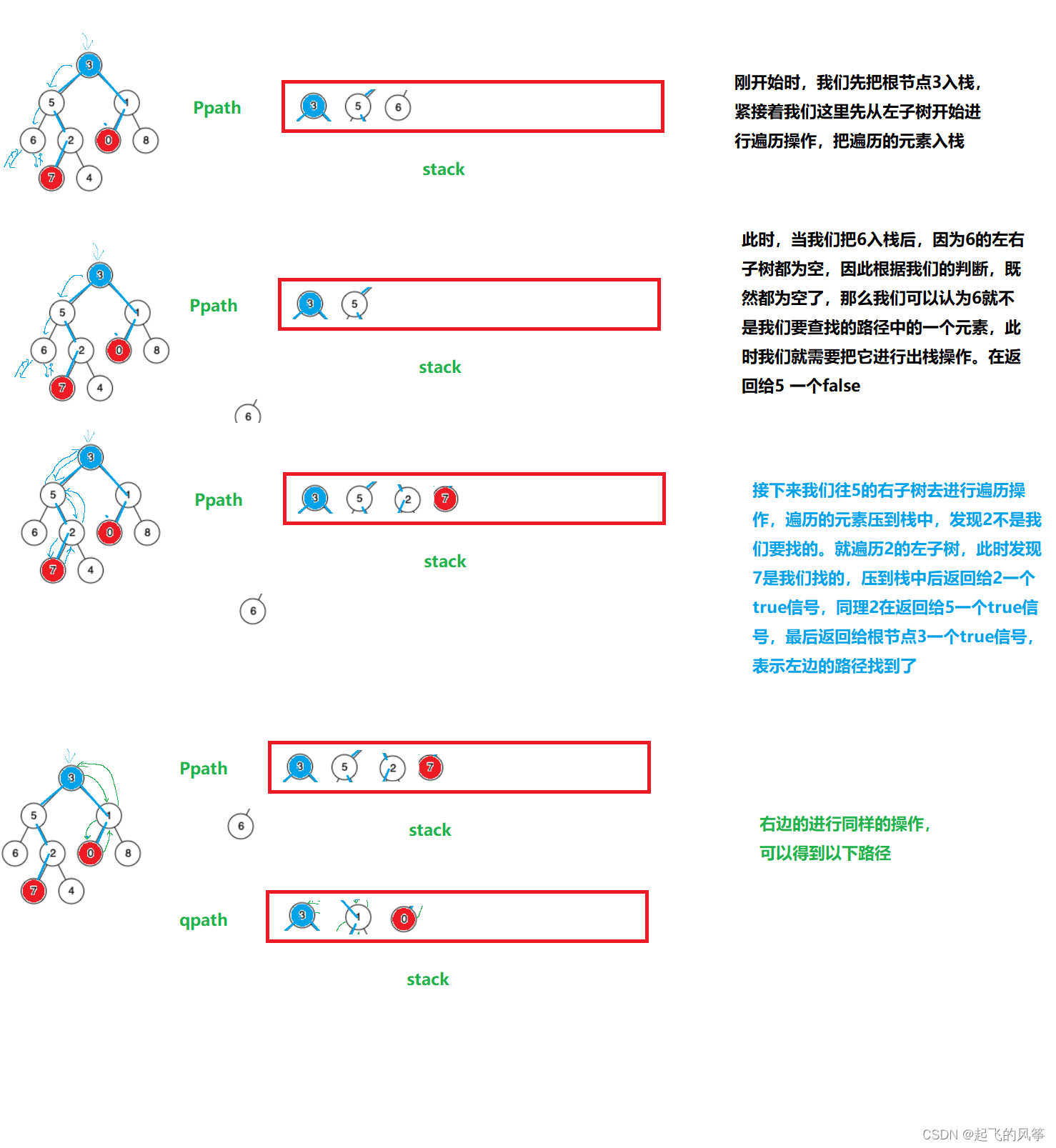
- 当我们成功的找到两端的路径之后,接下来就是判断步奏了:

💥代码展示:
class Solution { public: bool Getpath(TreeNode* root,TreeNode* x, stack<TreeNode*>& path) { if( root == nullptr ) return false; path.push(root); if(root == x) return true; if(Getpath(root->left,x,path)) return true; if(Getpath(root->right,x,path)) return true; path.pop(); return false; } TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) { stack<TreeNode*>Ppath,qpath; Getpath(root,p,Ppath); Getpath(root,q,qpath); while(Ppath.size() != qpath.size()) { if(Ppath.size() > qpath.size()) { Ppath.pop(); } else qpath.pop(); } while(Ppath.top() != qpath.top()) { Ppath.pop(); qpath.pop(); } return Ppath.top(); } };- 最终结果:
思路二:
- 首先刚开始从根节点开始遍历,如果p和q中的任一个和root匹配,那么root就是最低公共祖先。
- 如果都不匹配,此时我们分别去递归左、右子树,如果有一个 节点出现在左子树,并且另一个节点出现在右子树,则root就是我们要找的值,即最低公共祖先
- 如果两个节点都出现在左子树,则说明最低公共祖先在左子树中,否则在右子树中。
💥代码展示:
class Solution { public: TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) { if( root == nullptr ) { return nullptr; } //如果p和q中的任一个和root匹配,那么root就是最进公共祖先 if( root == p || root == q ) { return root; } //如果都不匹配,则分别递归左、右子树 TreeNode* left = lowestCommonAncestor( root->left , p , q ); TreeNode* right = lowestCommonAncestor( root->right , p , q ); //如果有一个节点出现在左子树,并且另一个节点出现在右子树,则root就是最低公共祖先. if( left != nullptr && right != nullptr ) { return root; } //如果两个节点都出现在左子树,则说明最低公共祖先在左子树中,否则在右子树 if( right == nullptr ) { return left; } return right; } };- 最终结果:

到此,便是本期题目的所有讲解内容了,希望对大家有所帮助!!!
