阅读量:4



目录:
3195.包含所有1的最小矩形面积I【中等】
题目描述:
给你一个二维 二进制 数组 grid。请你找出一个边在水平方向和竖直方向上、面积 最小 的矩形,并且满足 grid 中所有的 1 都在矩形的内部。
返回这个矩形可能的 最小 面积。
示例 1:
输入: grid = [[0,1,0],[1,0,1]]
输出: 6
解释:
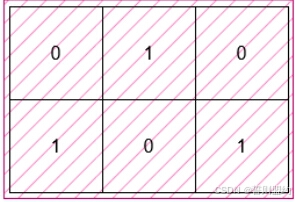
这个最小矩形的高度为 2,宽度为 3,因此面积为 2 * 3 = 6
示例 2:
输入: grid = [[0,0],[1,0]]
输出: 1
解释:
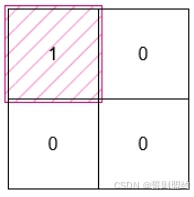
这个最小矩形的高度和宽度都是 1,因此面积为 1 * 1 = 1。
提示:
1 <= grid.length, grid[i].length <= 1000grid[i][j]是 0 或 1。- 输入保证
grid中至少有一个 1 。
题目分析:
求矩形面积,也就是在找最左边的1的列号firstCol,最右边的1列号lastCol,最上面1的行号firstRow,最下面1的行号lastRow。
那么面积就是 (lastRow-firstRow+1)*(lastCol-firstCol+1)
遍历矩阵,分别找第一列,最后一列,第一行,最后一行出现1的数据,然后计算求结果。
代码实现:
class Solution: def minimumArea(self, grid: List[List[int]]) -> int: rowNums = len(grid) colNums = len(grid[0]) firstRow = -1 firstCol = -1 lastRow = -1 lastCol = -1 for row in range(rowNums): if firstRow==-1: for col in range(colNums): if grid[row][col]==1: if firstRow==-1: firstRow=row break for col in range(colNums): if firstCol==-1: for row in range(rowNums): if grid[row][col]==1: if firstCol==-1: firstCol=col break for row in range(rowNums-1,-1,-1): if lastRow==-1: for col in range(colNums-1,-1,-1): if grid[row][col]==1: if lastRow==-1: lastRow=row break for col in range(colNums-1,-1,-1): if lastCol==-1: for row in range(rowNums-1,-1,-1): if grid[row][col]==1: if lastCol==-1: lastCol=col break value = (lastRow-firstRow+1)*(lastCol-firstCol+1) return value

总结:
详解:
- 首先,定义了网格的行数
rowNums和列数colNums。 - 然后,通过四个循环分别找到值为 1 的单元格首次出现的行
firstRow和列firstCol,以及最后出现的行lastRow和列lastCol。- 在第一个循环中,从第一行开始逐行查找,当找到第一个值为 1 的单元格时,记录其所在的行
firstRow,并结束内层循环。 - 第二个循环类似,从第一列开始逐列查找,记录第一个值为 1 的单元格所在的列
firstCol。 - 第三个循环从最后一行开始逐行向前查找,记录最后一个值为 1 的单元格所在的行
lastRow。 - 第四个循环从最后一列开始逐列向前查找,记录最后一个值为 1 的单元格所在的列
lastCol。
- 在第一个循环中,从第一行开始逐行查找,当找到第一个值为 1 的单元格时,记录其所在的行
- 最后,根据找到的边界计算最小矩形区域的面积
value,公式为(lastRow - firstRow + 1) * (lastCol - firstCol + 1)。
考点:
- 对二维数组的遍历和操作。
- 循环的使用和条件判断。
- 如何确定一个区域的边界。
收获:
- 加深对二维数组操作的理解,包括如何遍历和根据特定条件获取相关信息。
- 学会通过多个循环和条件判断来确定一个区域的边界,并计算其相关属性(如面积)。
- 提高在解决实际问题时,对问题进行分析和转化为代码实现的能力。

